- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии теорема о трех перпендикулярах
Содержание
- 1. Презентация по геометрии теорема о трех перпендикулярах
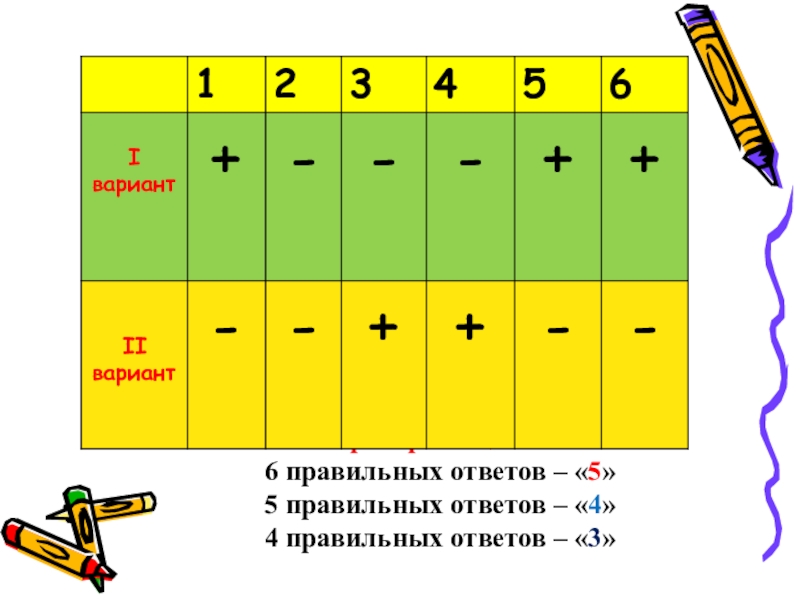
- 2. Критерии оценок 6 правильных ответов – «5»
- 3. Основные понятияАНМаАМ -АН - МН
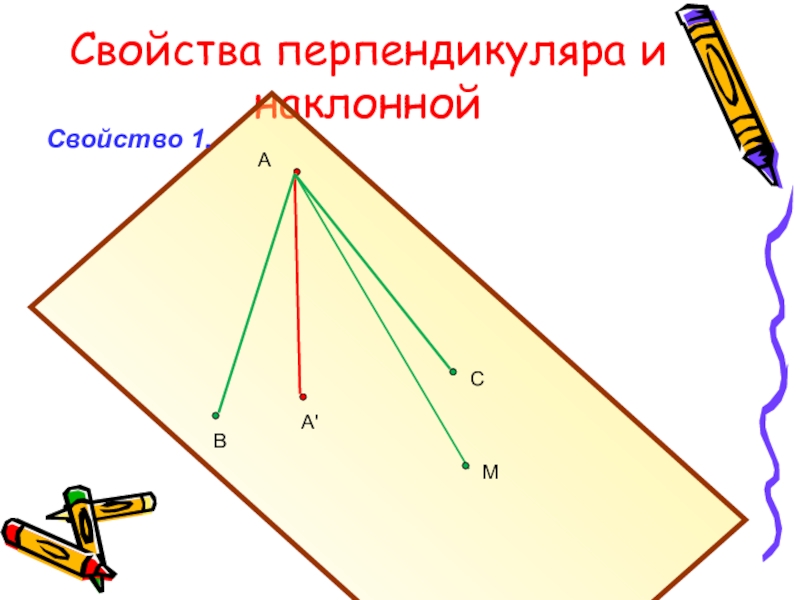
- 4. Свойства перпендикуляра и наклоннойАВА'СМСвойство 1.
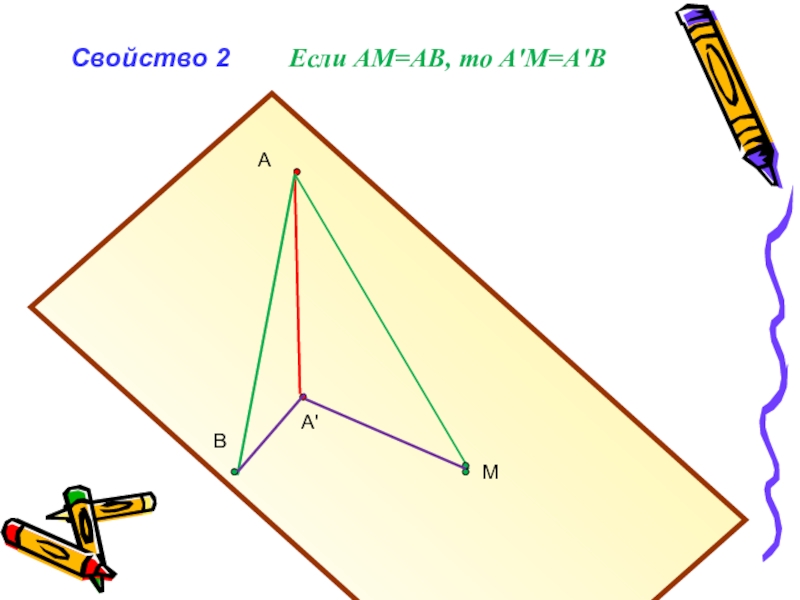
- 5. АВА'МСвойство 2Если АМ=АВ, то А'М=А'В
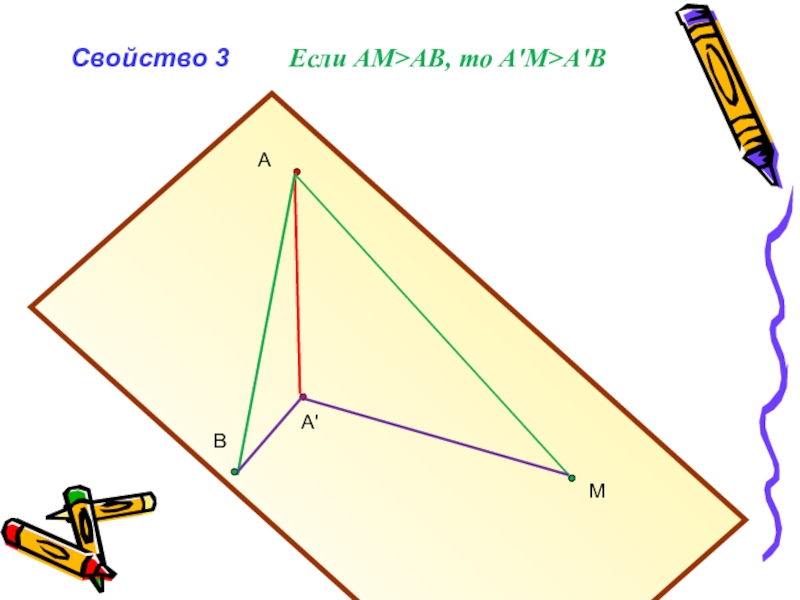
- 6. АВА'МСвойство 3Если АМ>АВ, то А'М>А'В
- 7. Теорема о трех перпендикулярахЕсли прямая, проведенная на
- 8. Теорема о трёх перпендикулярахАН ⊥ НМ -
- 9. Справедлива также и обратная теорема (сформулируйте сами)Доказательство:АН
- 10. Установите по рисункам положение прямых а и вАВСD – прямоугольник,BF⊥(ABC)АВСD – прямоугольник,BF⊥(ABC)КК
- 11. Установите по рисункам положение прямых а и вАВСDFbaАВСD – ромб,BF⊥(ABC)АВСD – ромб,BF⊥(ABC)О
- 12. Задачи на построениеОтрезок МС перпендикулярен плоскости равностороннего
- 13. Отрезок MD перпендикулярен плоскости прямоугольника ABCD. Проведите через точку М перпендикуляры к прямым ВС и АВBACDM
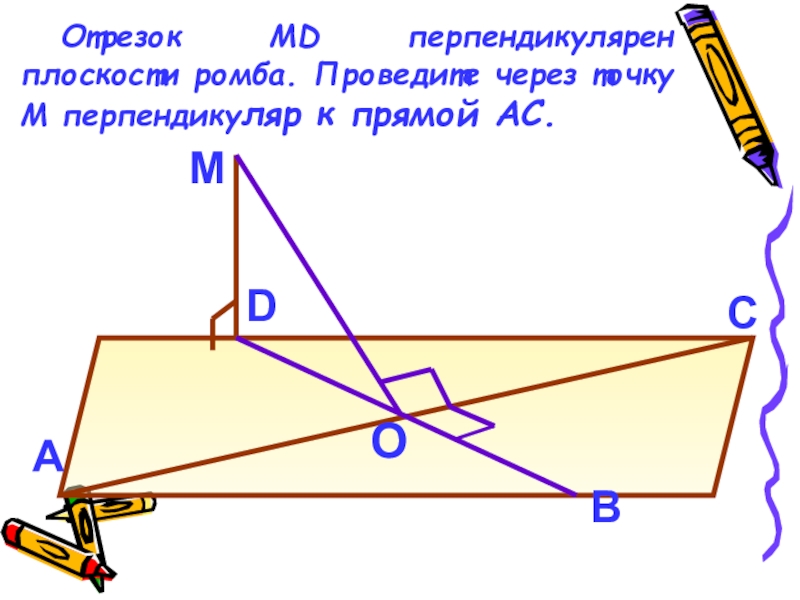
- 14. Отрезок МD перпендикулярен плоскости ромба. Проведите через точку М перпендикуляр к прямой AC.BACDMO
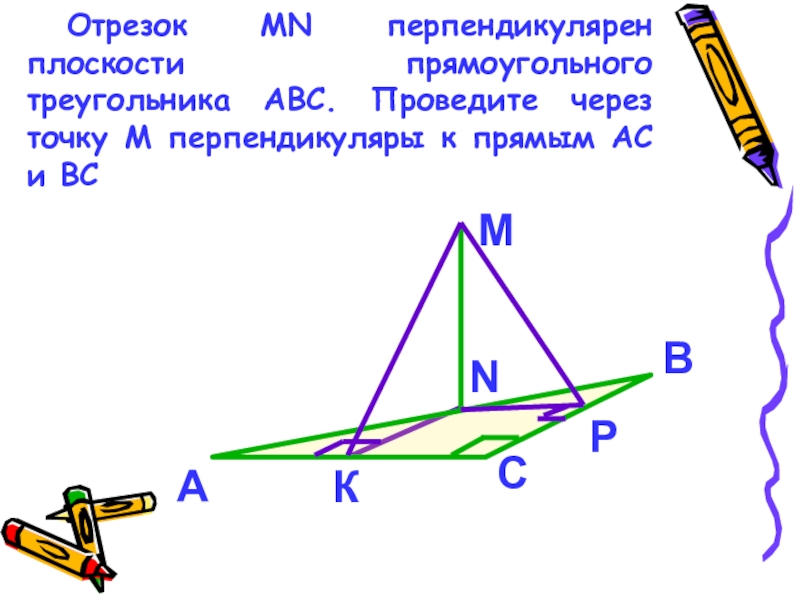
- 15. Отрезок MN перпендикулярен плоскости прямоугольного треугольника АВС.
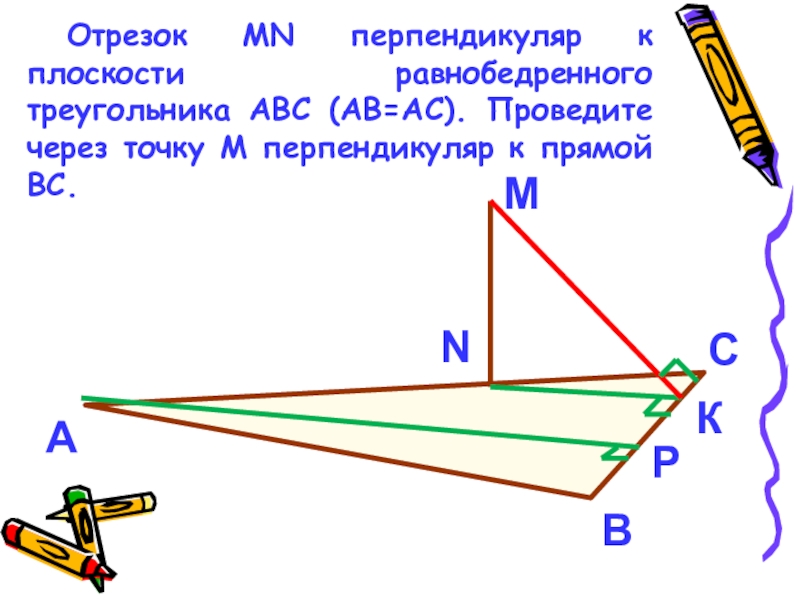
- 16. Отрезок MN перпендикуляр к плоскости равнобедренного треугольника
- 17. «Если вы хотите научиться плавать, то смело
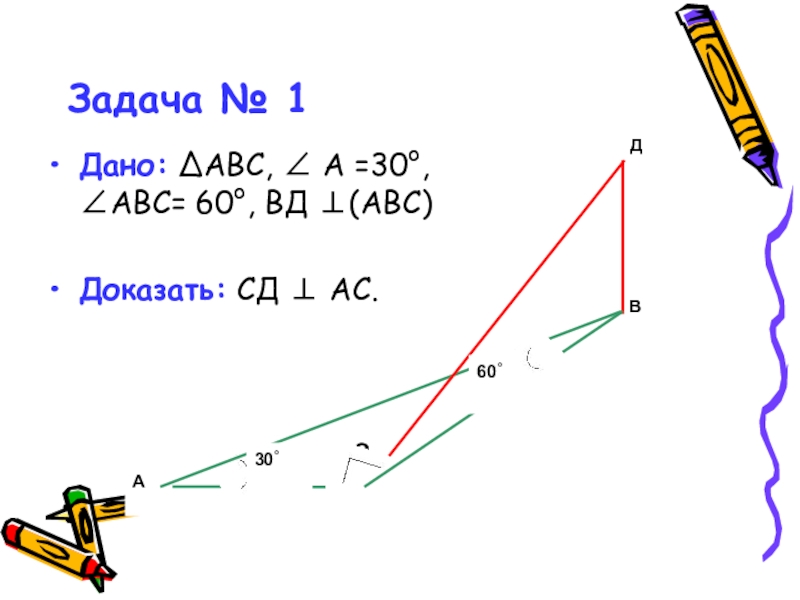
- 18. Задача № 1Дано: ΔАВС, ∠ А =30°, ∠АВС= 60°, ВД ⊥(АВС) Доказать: СД ⊥ АС.
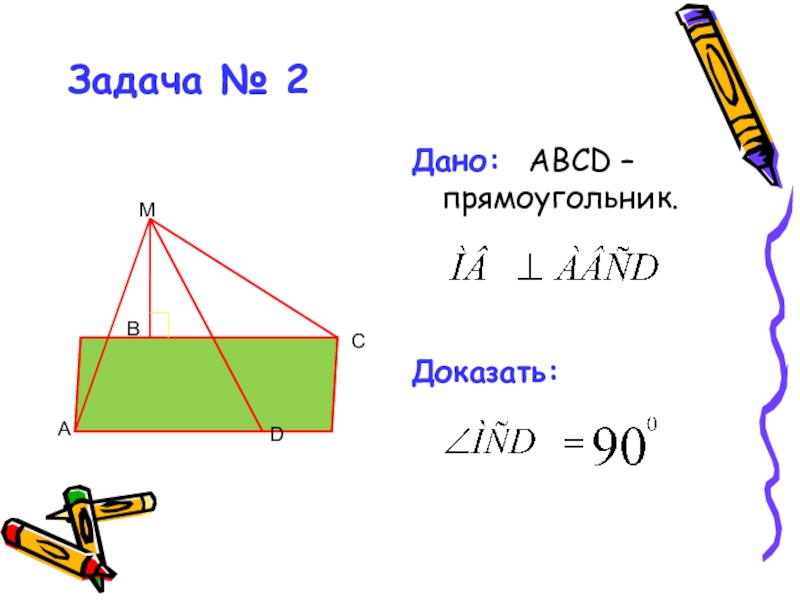
- 19. Задача № 2Дано: АВСD –прямоугольник.Доказать:С
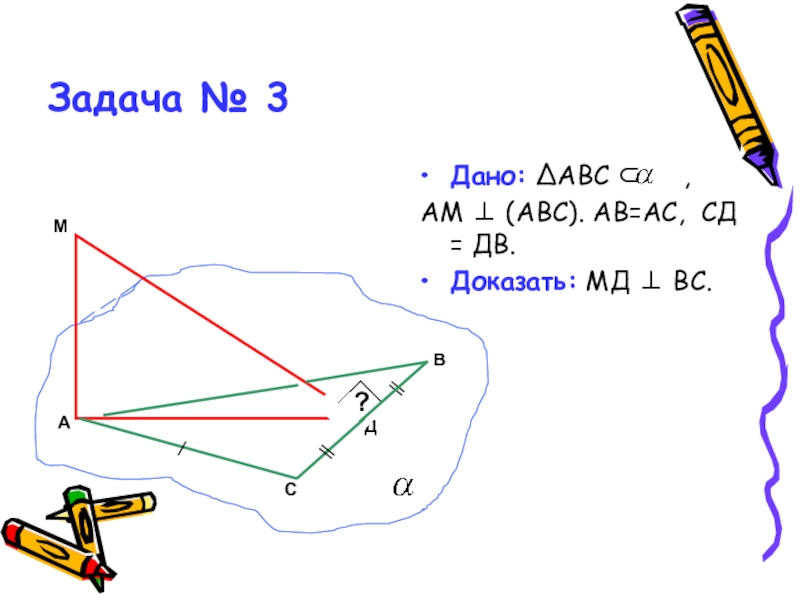
- 20. Задача № 3Дано: ΔАВС ⊂
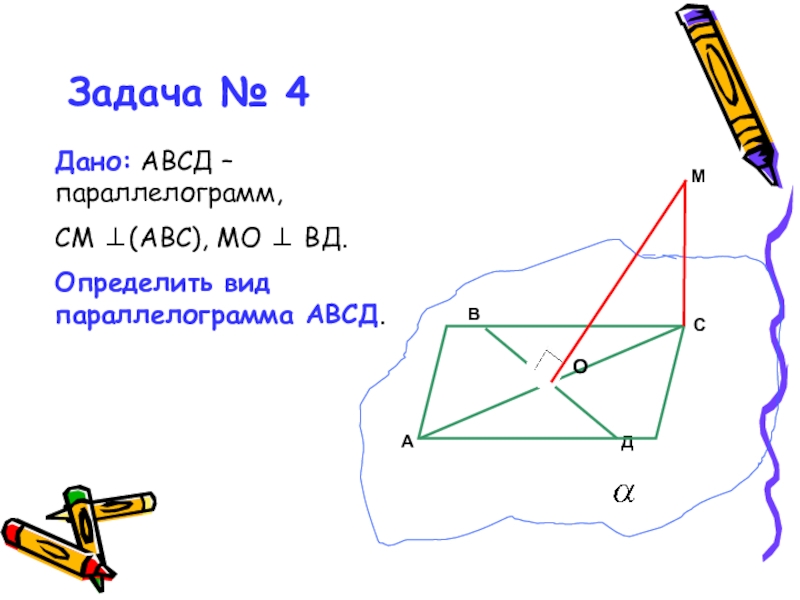
- 21. Задача № 4Дано: АВСД – параллелограмм, СМ ⊥(АВС), МО ⊥ ВД.Определить вид параллелограмма АВСД.
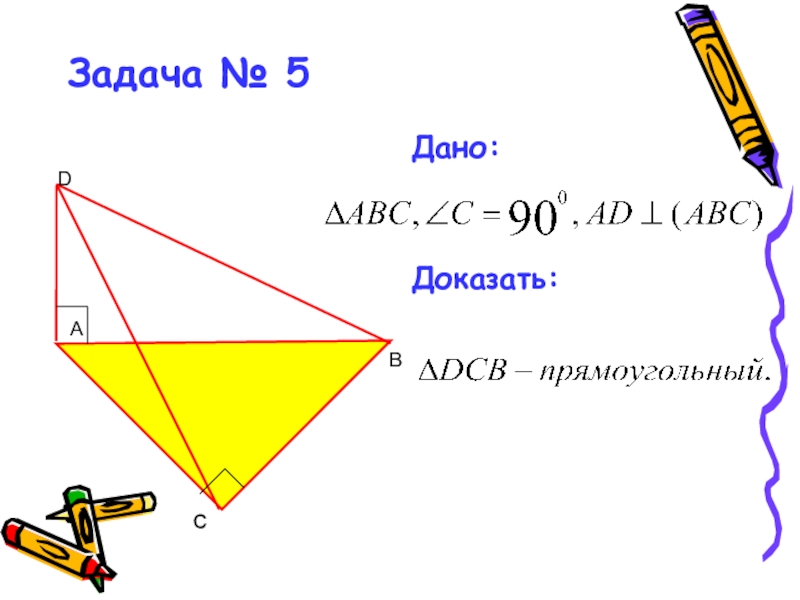
- 22. Задача № 5Дано:Доказать:C
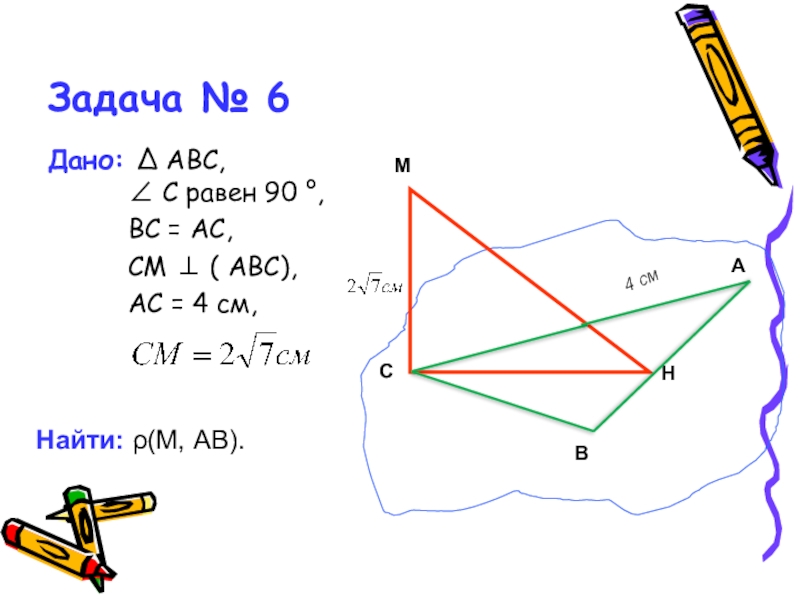
- 23. Задача № 6Дано: Δ АВС, ∠ С равен
- 24. Дано: Δ АВС, ∠ С = 90°, АД
- 25. Задача № 8Дано: АВСД - ромб,ВМ ⊥
Критерии оценок 6 правильных ответов – «5» 5 правильных ответов – «4» 4 правильных ответов – «3»
Слайд 2Критерии оценок 6 правильных ответов – «5» 5 правильных ответов – «4» 4 правильных
ответов – «3»
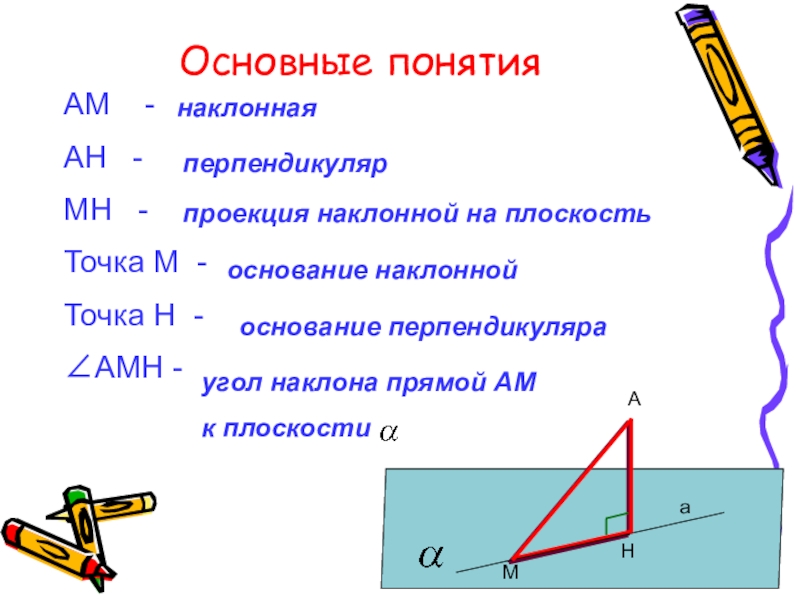
Слайд 3Основные понятия
А
Н
М
а
АМ -
АН -
МН -
Точка М -
Точка
Н -
∠АМН -
∠АМН -
наклонная
перпендикуляр
проекция наклонной на плоскость
основание наклонной
основание перпендикуляра
угол наклона прямой АМ
к плоскости
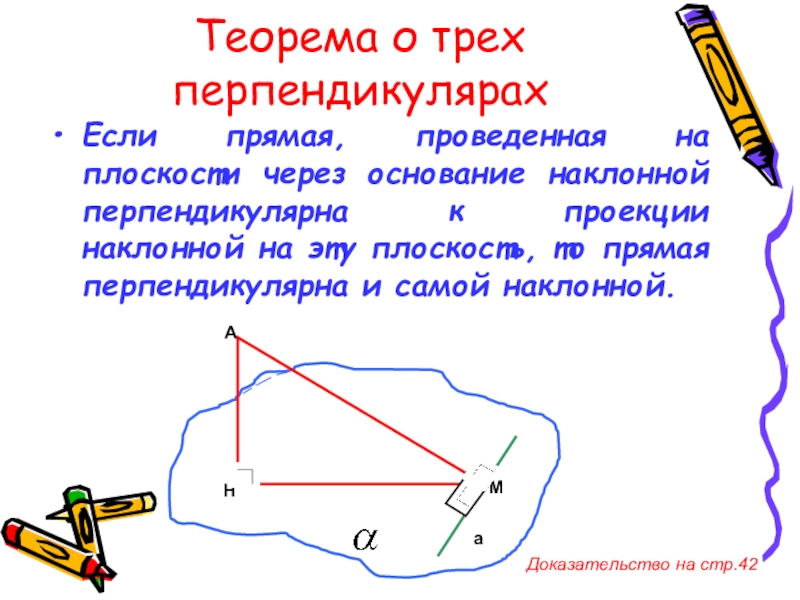
Слайд 7Теорема о трех перпендикулярах
Если прямая, проведенная на плоскости через основание наклонной
перпендикулярна к проекции наклонной на эту плоскость, то прямая перпендикулярна и самой наклонной.
Доказательство на стр.42
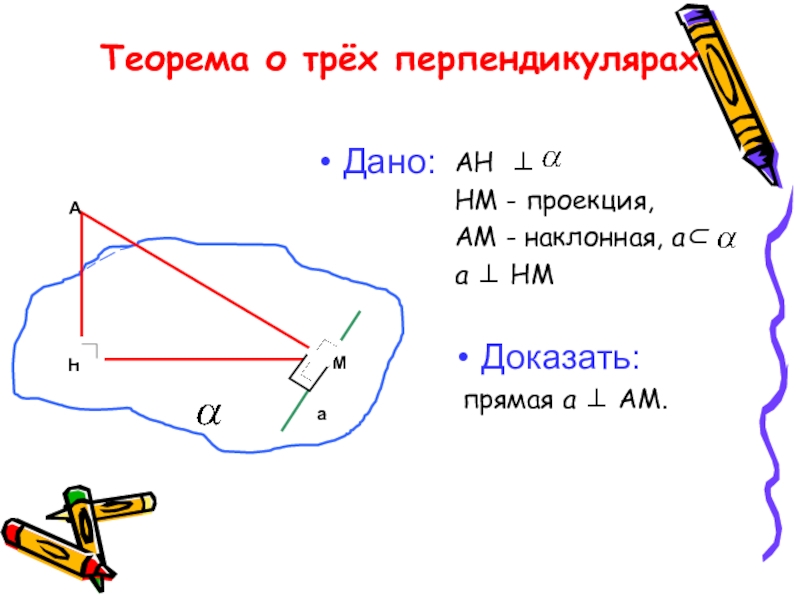
Слайд 8Теорема о трёх перпендикулярах
АН ⊥
НМ - проекция,
АМ - наклонная,
а⊂
а ⊥ НМ
прямая а ⊥ АМ.
а ⊥ НМ
прямая а ⊥ АМ.
Дано:
Доказать:
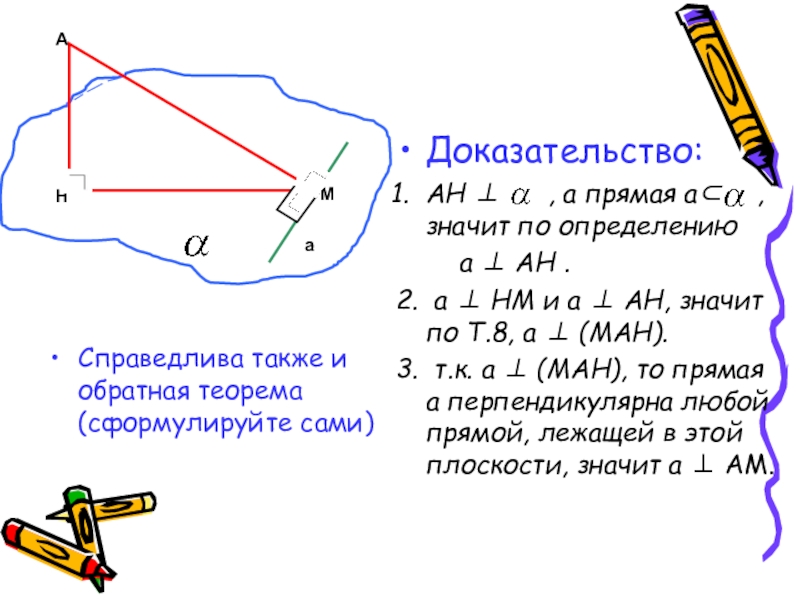
Слайд 9
Справедлива также и обратная теорема (сформулируйте сами)
Доказательство:
АН ⊥ ,
а прямая а⊂ , значит по определению
а ⊥ АН .
2. а ⊥ НМ и а ⊥ АН, значит по Т.8, а ⊥ (МАН).
3. т.к. а ⊥ (МАН), то прямая а перпендикулярна любой прямой, лежащей в этой плоскости, значит а ⊥ АМ.
а ⊥ АН .
2. а ⊥ НМ и а ⊥ АН, значит по Т.8, а ⊥ (МАН).
3. т.к. а ⊥ (МАН), то прямая а перпендикулярна любой прямой, лежащей в этой плоскости, значит а ⊥ АМ.
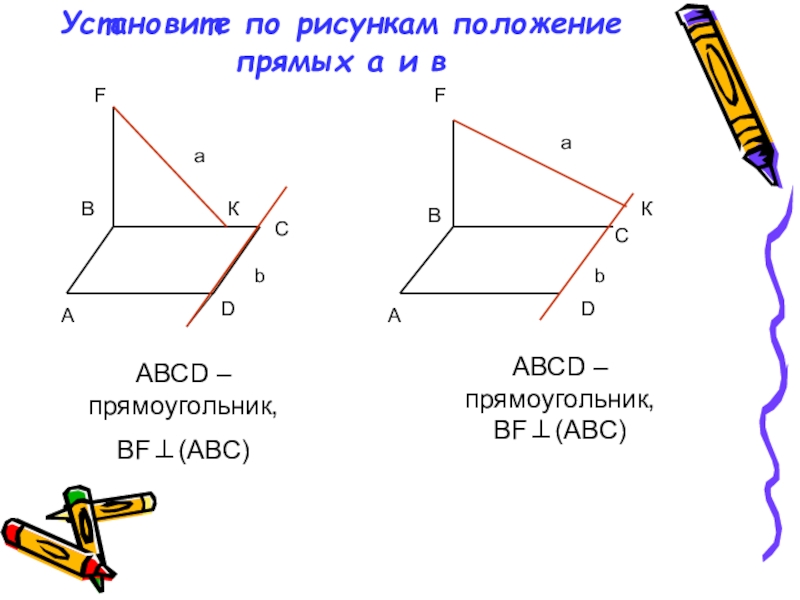
Слайд 10Установите по рисункам положение прямых а и в
АВСD – прямоугольник,
BF⊥(ABC)
АВСD –
прямоугольник,
BF⊥(ABC)
BF⊥(ABC)
К
К
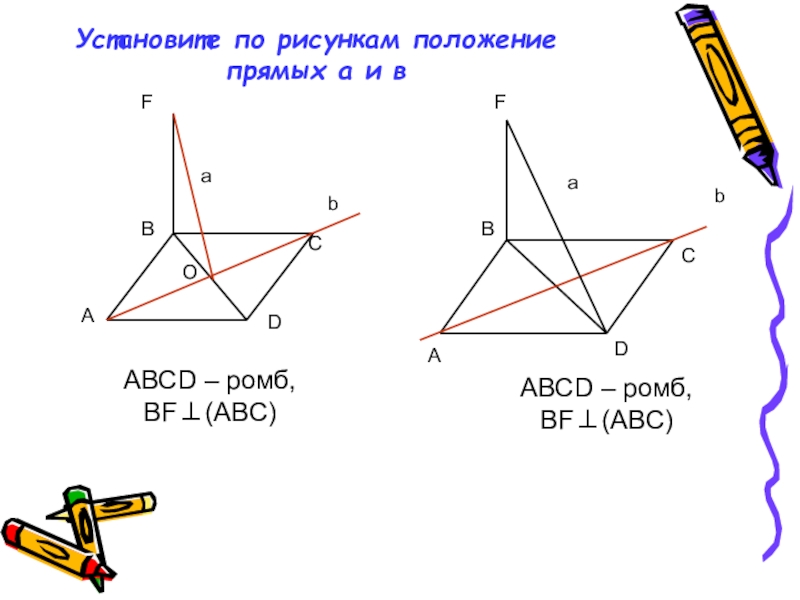
Слайд 11Установите по рисункам положение прямых а и в
А
В
С
D
F
b
a
АВСD – ромб,
BF⊥(ABC)
АВСD –
ромб,
BF⊥(ABC)
BF⊥(ABC)
О
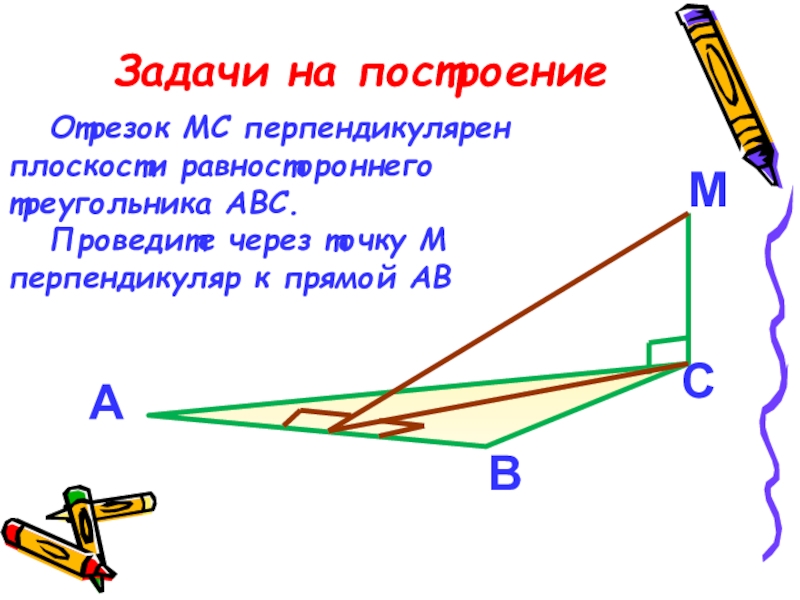
Слайд 12Задачи на построение
Отрезок МС перпендикулярен плоскости равностороннего треугольника АВС.
Проведите через
точку М перпендикуляр к прямой АВ
B
А
С
М
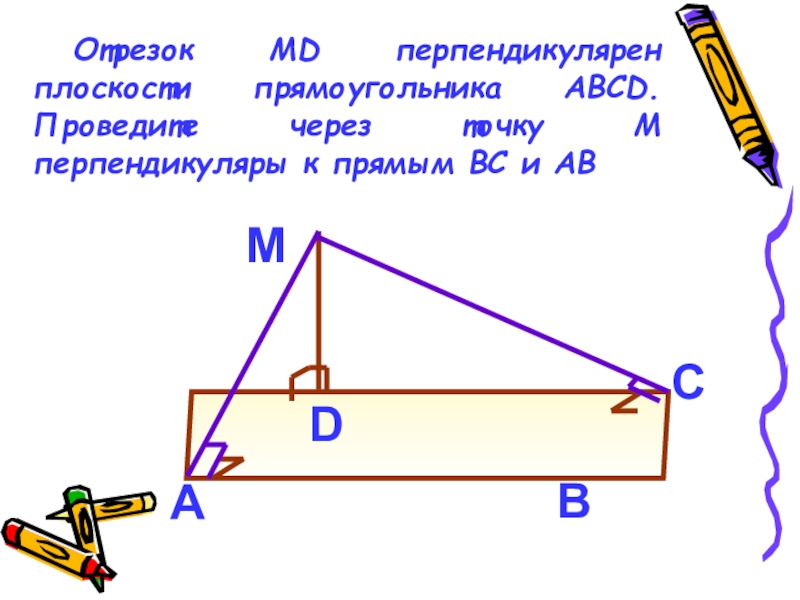
Слайд 13Отрезок MD перпендикулярен плоскости прямоугольника ABCD. Проведите через точку М перпендикуляры
к прямым ВС и АВ
B
A
C
D
M
Слайд 14Отрезок МD перпендикулярен плоскости ромба. Проведите через точку М перпендикуляр к
прямой AC.
B
A
C
D
M
O
Слайд 15Отрезок MN перпендикулярен плоскости прямоугольного треугольника АВС. Проведите через точку М
перпендикуляры к прямым АС и ВС
C
B
A
M
N
К
Р
Слайд 16Отрезок MN перпендикуляр к плоскости равнобедренного треугольника АВС (АВ=АС). Проведите через
точку М перпендикуляр к прямой ВС.
A
В
С
М
N
К
Р
Слайд 17«Если вы хотите научиться плавать, то смело входите в воду, а
если хотите научиться решать задачи, то решайте их».
Д.Пойа
Слайд 21Задача № 4
Дано: АВСД – параллелограмм,
СМ ⊥(АВС), МО ⊥ ВД.
Определить
вид параллелограмма АВСД.
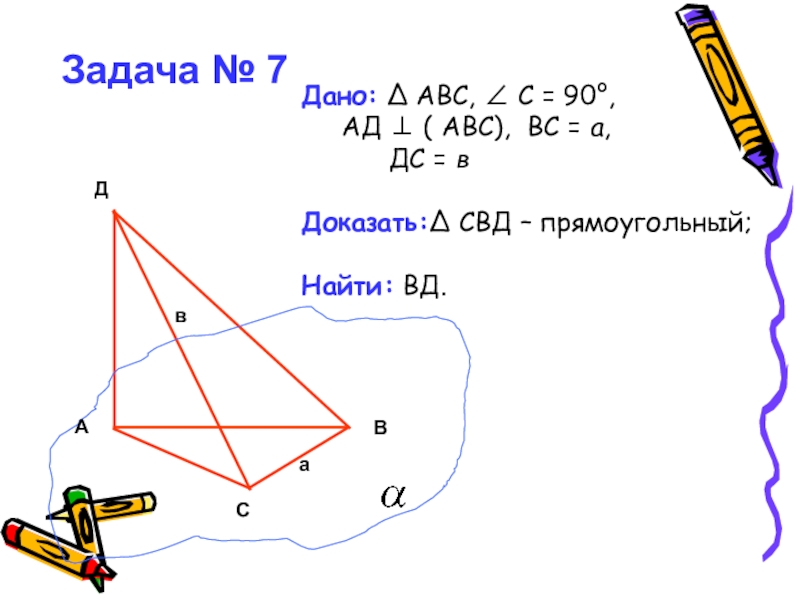
Слайд 24Дано: Δ АВС, ∠ С = 90°,
АД ⊥ ( АВС), ВС
= а,
ДС = в
Доказать:Δ СВД – прямоугольный;
Найти: ВД.
ДС = в
Доказать:Δ СВД – прямоугольный;
Найти: ВД.
Задача № 7
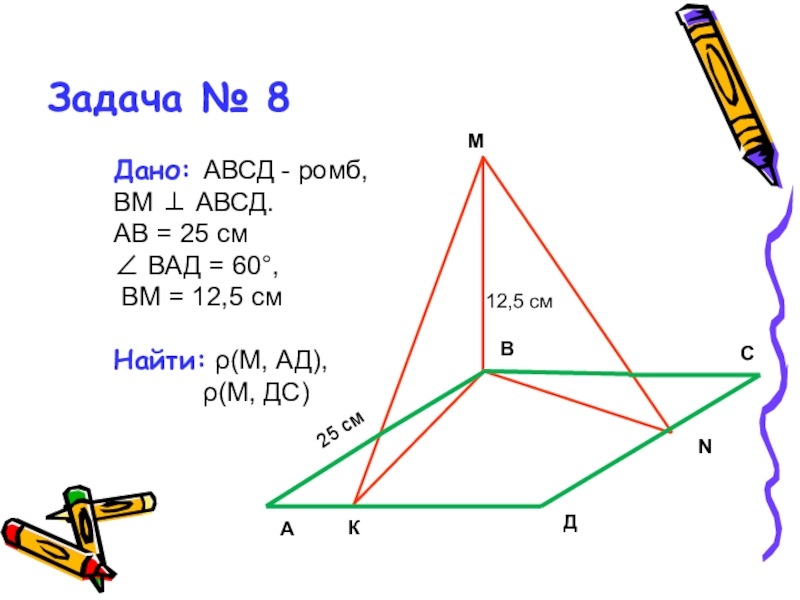
Слайд 25Задача № 8
Дано: АВСД - ромб,
ВМ ⊥ АВСД.
АВ = 25
см
∠ ВАД = 60°,
ВМ = 12,5 см
Найти: ρ(М, АД),
ρ(М, ДС)
∠ ВАД = 60°,
ВМ = 12,5 см
Найти: ρ(М, АД),
ρ(М, ДС)
N
К
