- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Теорема Менелая (10 класс)
Содержание
- 1. Презентация по геометрии Теорема Менелая (10 класс)
- 2. СодержаниеБиография ученогоФормулировка теоремыДоказательство теоремыЗадачи
- 3. Биография ученогоМенелай Александрийский (Menélaos), древнегреческий астроном и
- 4. Формулировка теоремыПусть на сторонах АВ, ВС ипродолжении
- 5. Доказательство теоремы МенелаяПредположим, что точки А1, В1
- 6. Задачи по теме: «Теорема Менелая»
- 7. Задача1В треугольнике АВС AD — медиана, точка
- 8. Решение задачи 1Пусть BD = DC =
- 9. Задача 2 В треугольнике АВС на стороне
- 10. Решение задачи 2По условию задачи МА =
- 11. Задача для самостоятельного решения Дано: точка К
- 12. Задача для самостоятельного решенияРешение. По условию
СодержаниеБиография ученогоФормулировка теоремыДоказательство теоремыЗадачи
Слайд 3Биография ученого
Менелай Александрийский (Menélaos), древнегреческий астроном и математик (1 в.). Автор
работ по сферической тригонометрии: 6 книг о вычислении хорд и 3 книги «Сферики» (сохранились в арабском переводе). Тригонометрия у Менелая отделена от геометрии и астрономии. Арабские авторы упоминают также о книге Менелая по гидростатике.
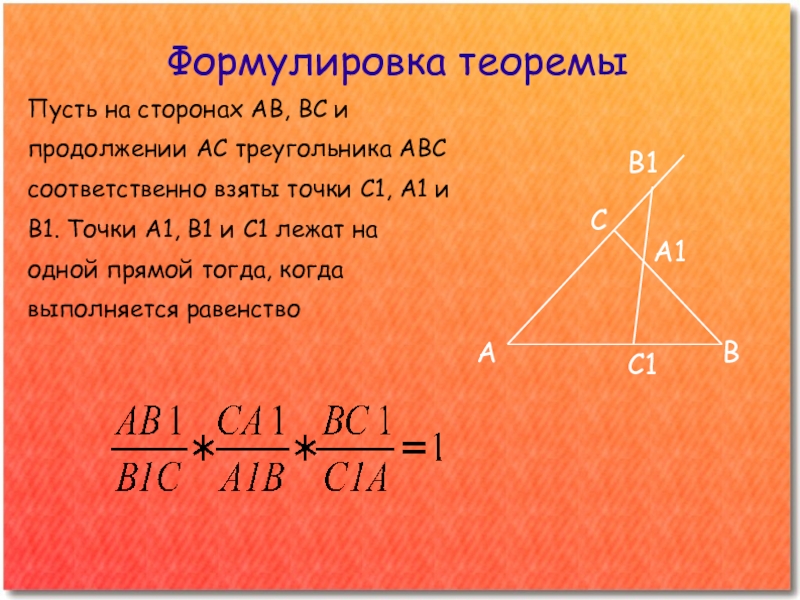
Слайд 4Формулировка теоремы
Пусть на сторонах АВ, ВС и
продолжении АС треугольника АВС
соответственно взяты
точки С1, А1 и
В1. Точки А1, В1 и С1 лежат на
одной прямой тогда, когда
выполняется равенство
В1. Точки А1, В1 и С1 лежат на
одной прямой тогда, когда
выполняется равенство
А
B
C
В1
С1
А1
Слайд 5Доказательство теоремы Менелая
Предположим, что точки А1, В1 и С1 принадлежат
одной прямой
а. Через вершину С треугольника
АВС проведем прямую параллельную а, и
обозначим через D точку ее пересечение с АВ.
Из подобия треугольников ADC и AC1B1 следует
выполнимость равенства
Аналогично, из подобия треугольников BDC и
ВС1А1 следует выполнимость равенства
Перемножая эти равенства получим равенство
Из которого следует, что
АВС проведем прямую параллельную а, и
обозначим через D точку ее пересечение с АВ.
Из подобия треугольников ADC и AC1B1 следует
выполнимость равенства
Аналогично, из подобия треугольников BDC и
ВС1А1 следует выполнимость равенства
Перемножая эти равенства получим равенство
Из которого следует, что
C
А
B
D
В1
А1
С1
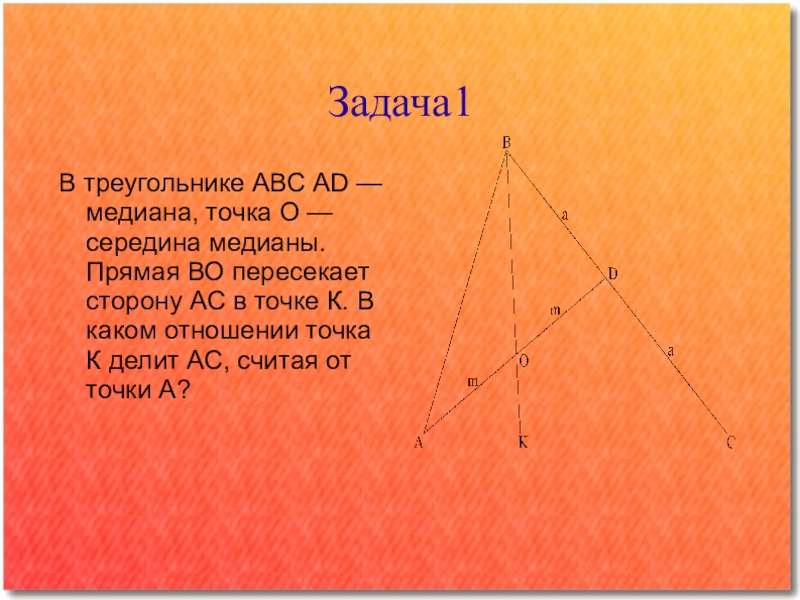
Слайд 7Задача1
В треугольнике АВС AD — медиана, точка О — середина медианы.
Прямая ВО пересекает сторону АС в точке К. В каком отношении точка К делит АС, считая от точки А?
Слайд 8Решение задачи 1
Пусть BD = DC = а, АО = OD
= m. Прямая ВK пересекает две стороны и продолжение третьей стороны треугольника ADC. По теореме Менелая
Ответ: 1 : 2.
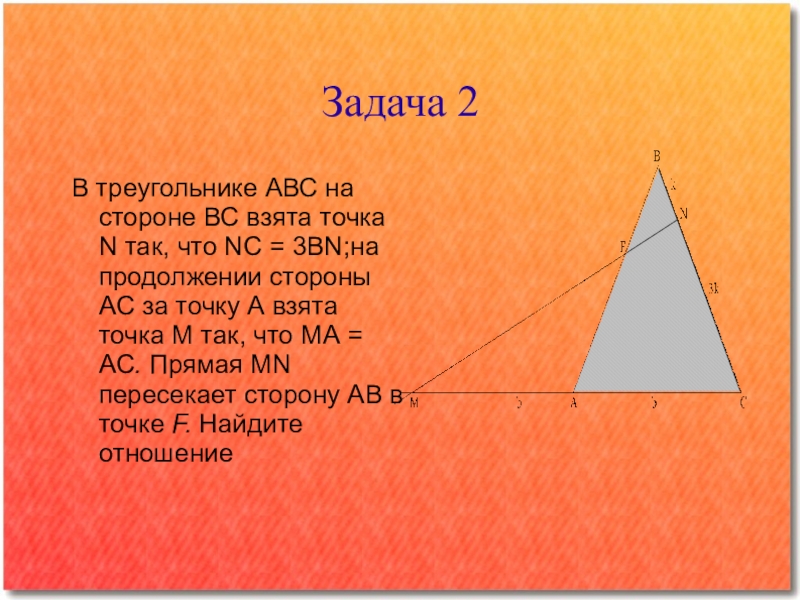
Слайд 9Задача 2
В треугольнике АВС на стороне ВС взята точка N
так, что NC = 3BN;на продолжении стороны АС за точку А взята точка М так, что МА = АС. Прямая MN пересекает сторону АВ в точке F. Найдите отношение
Слайд 10Решение задачи 2
По условию задачи МА = AC, NC =3BN. Пусть
МА = АС = b, BN =k, NC = 3k. Прямая MN пересекает две стороны .треугольника АВС и продолжение третьей. По теореме Менелая
Ответ: 2 : 3.
Ответ: 2 : 3.
Слайд 11Задача для самостоятельного
решения
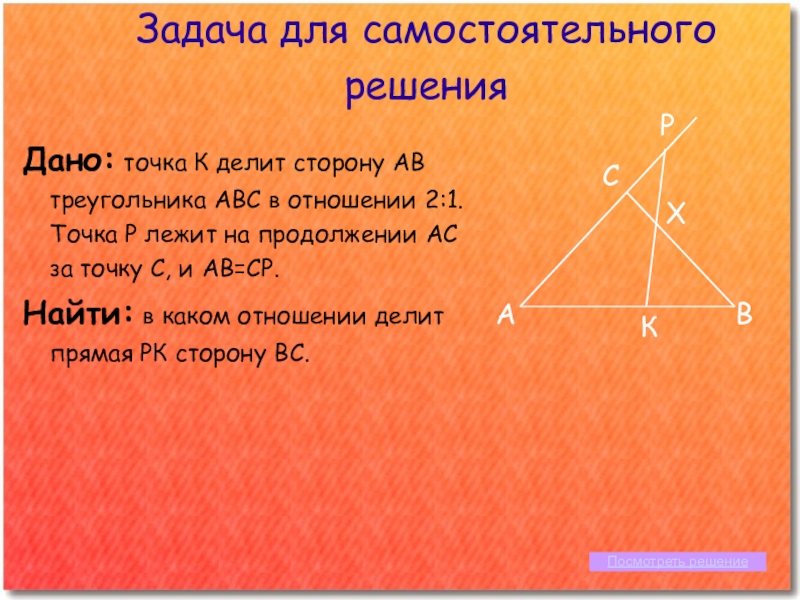
Дано: точка К делит сторону АВ треугольника АВС
в отношении 2:1. Точка Р лежит на продолжении АС за точку С, и АВ=СР.
Найти: в каком отношении делит прямая РК сторону ВС.
Найти: в каком отношении делит прямая РК сторону ВС.
Посмотреть решение
А
В
С
Х
Р
К
Слайд 12Задача для самостоятельного
решения
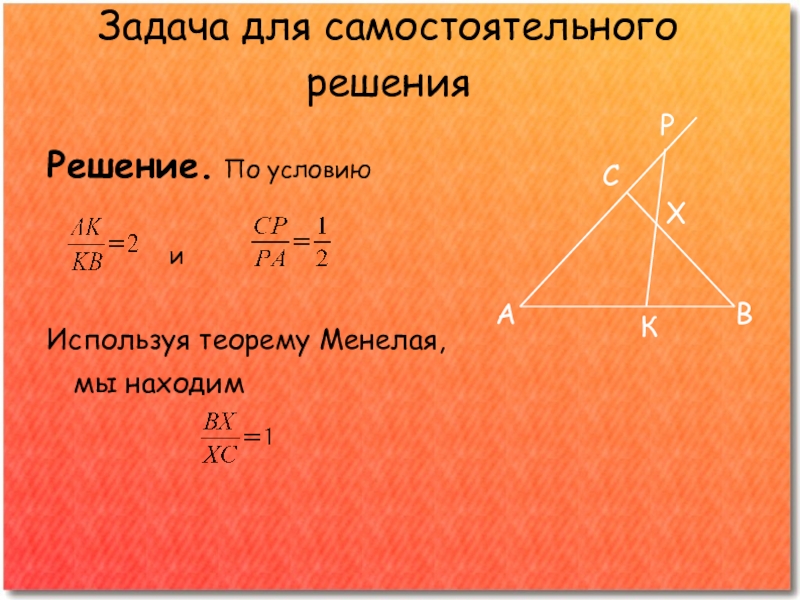
Решение. По условию
и
Используя теорему Менелая, мы находим
Используя теорему Менелая, мы находим
А
В
С
Х
Р
К