- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Тела вращения (проектная деятельность 11 класс)
Содержание
- 1. Презентация по геометрии Тела вращения (проектная деятельность 11 класс)
- 2. Краткая аннотация проекта Проект " Магия тел
- 3. Введение Форму тел вращения имеют многие детали
- 4. Учебный проект с точки зрения учащегося -
- 5. Учебный проект с точки зрения учителя -
- 6. Цели проекта: совершенствование навыков исследовательской работы; формирование
- 7. Задачи проекта: Учебные задачи:- научить учащихся самостоятельно
- 8. Вопросы, направляющие проект Основополагающий вопросПочему планеты имеют
- 9. План проведения проекта Формулирование темы проекта,
- 10. Этапы проектной деятельности: 1. Организационный -
- 11. Направления исследования. Теоретики-математики (проблемные вопросы с научной
- 12. Подготовка учащихся к работе над проектом.
- 13. Выполнение проекта. Этот этап включает в
- 14. Презентация проектов. Весь подготовленный, оформленный материал надо представить одноклассникам, защитить свой проект.
- 15. Подведение итогов проектной работы. Вопросы для
- 16. Творческие задания групп были выполнены следующим образом:
- 17. Творческие задания групп (презентации)
- 18. Группа "Практиков" Тела вращения в архитектуре
- 19. Слайд 19
- 20. Тела вращения в быту и природе
- 21. Слайд 21
- 22. Конус (моллюск) Яд конуса (Conus magus) применяется
- 23. Слайд 23
- 24. кроссворд "тела и фигуры вращения" По горизонтали.
- 25. Ответы к кроссворду .КУПЛК Р
- 26. Тест 1 вариантДиагональ осевого сечения цилиндра равна
- 27. Ответы к тесту1вариантвбввб2вариантгвбгв
- 28. Группы "Теоретиков-математиков"ЦилиндрШарКонусВИДЫ ТЕЛ ВРАЩЕНИЯ:
- 29. ОПРЕДЕЛЕНИЕ КОНУСА Конус-тело вращения состоящее из круга,
- 30. ОПРЕДЕЛЕНИЕ ЦИЛИНДРА Цилиндр-тело, которое состоит из двух
- 31. ОПРЕДЕЛЕНИЕ ШАРА Шаром называется тело, которое состоит
- 32. Слайд 32
- 33. Слайд 33
- 34. СЕЧЕНИЯ ЦИЛИНДРА Сечение цилиндра плоскостью , параллельной
- 35. СЕЧЕНИЕ КОНУСА Сечение конуса плоскостью , проходящей
- 36. СЕЧЕНИЯ ШАРА Сечение шара плоскостью -круг. Центр
- 37. Слайд 37
- 38. Аналитическая геометрияВ аналитической геометрии геометрические объекты
- 39. Группы "Историков"Московский математический папирусЭто один из древнейших
- 40. Задача № 10 Московского папирусаСвязана с вычислением
- 41. Греч. (конос) --- конус, сосновая
- 42. Архиме́д287 – 212 гг. до н.э.
- 43. Легенда об Архимеде Архимед служил у царя
- 44. Гиерон поручил Архимеду проверить честность мастера. Ученый
- 45. Корона вытеснила воды больше, чем слиток
- 46. Конус выхода для гамма-лучей Солнца
- 47. Неевклидовы геометрииСферическая геометрия — раздел геометрии, изучающий геометрические фигуры на поверхности сферы.
- 48. Процесс формирования планеты изначально начинается с появления
- 49. В психологических исследованиях рефлексия выступает двояко:как способ
- 50. Заключение Основная задача проекта состоит не только
- 51. Выводы.Реализация проектного и исследовательского методов на практике
- 52. Спасибо за внимание !
Слайд 1УЧЕБНЫЙ ПРОЕКТ
по геометрии
«Магия тел вращения»
Учитель математики Косинец Е. В.
ГБОУ
Санкт-Петербурга.
Слайд 2Краткая аннотация проекта
Проект " Магия тел вращения " рассчитан на учащихся
Настоящий проект направлен на поиск новых идей в преподавании геометрии в 11 классе.
Проект предполагает творческое освоение ребятами ряда учебных тем. А именно: ввести понятия цилиндрической и конической поверхности, цилиндра, конуса, шара (сферы) и их элементов, тел вращения второго порядка. Вывести формулы для вычисления площадей полной и боковой поверхностей и площади сферы, формулы вычисления объемов цилиндра, конуса, шара.
В рамках проекта учащиеся находят математическое обоснование геометрических тайн Земли и других планет солнечной системы, узнают о связи тел вращения между собой, уточняют возможности применения форм данных геометрических тел в современном мире.
Проект способствует подготовке учащихся к сдаче ЕГЭ по математике.
Проект предполагает самостоятельное изучение тем, работу в парах или небольших группах.
Слайд 3Введение
Форму тел вращения имеют многие детали машин, приборов. При обработке металла
Телами вращения являются и изделия гончарного производства; так, гончар помещает кусок глины на середину вращающегося рабочего стола и, прижимая к нему деревянный или металлический шаблон, придаёт этому куску глины нужную форму.
Планета Земля и другие планеты имеют форму тела вращения.
Слайд 4Учебный проект с точки зрения учащегося -
это возможность делать что-то
это деятельность, позволяющая проявить себя, попробовать свои силы, приложить свои знания, принести пользу и показать публично достигнутый результат;
это деятельность, направленная на решение интересной проблемы, сформулированной самими учащимися в виде цели и задачи, когда результат этой деятельности - найденный способ решения проблемы - носит практический характер, имеет важное прикладное значение и, что весьма важно, интересен и значим для самих открывателей.
Слайд 5Учебный проект с точки зрения учителя -
- это дидактическое средство,
В рамках проекта учащиеся изучают тела вращения, такие как цилиндр, конус и шар, находят математическое обоснование геометрических тайн Земли и других планет солнечной системы, узнают о связи тел вращения между собой, уточняют возможности применения форм данных геометрических тел в современном мире.
Слайд 6Цели проекта:
совершенствование навыков исследовательской работы;
формирование исследовательской компетентности;
углубление
формирование умения работать с информацией, находить источники, из которых ее можно почерпнуть;
формирование умения проводить исследования, передавать и презентовать полученные знания и опыт;
формирование навыков совместной работы и делового общения в группах.
Слайд 7Задачи проекта:
Учебные задачи:
- научить учащихся самостоятельно добывать и осмысливать знания для
- развивать навыки самоутверждения, самооценки.
-способствовать развитию творческой деятельности.
Развивающие задачи:
- развивать творческую сторону мышления;
- учить осуществлять исследовательскую деятельность;
- развивать интеллектуальные способности учащихся;
- развивать правильную математическую речь.
Воспитательные задачи:
- вовлечь учащихся в посильную для каждого, но обязательно активную познавательную деятельность при работе над проектом.
- продолжить формирование навыков общения.
Слайд 8Вопросы, направляющие проект
Основополагающий вопрос
Почему планеты имеют форму шара?
Проблемные вопросы
Как получаются
Как изображают объемные тела вращения?
Учебные вопросы
Что такое тела вращения?
Какие тела вращения вы знаете?
Как посчитать площади поверхности и объемы тел вращения?
Где мы можем увидеть тела вращения?
Как используются тела вращения в искусстве, архитектуре и пр.?
Слайд 9План проведения проекта
Формулирование темы проекта, его целей, задач.
Составление
Этапы реализации проекта:
Знакомство с проектом (вводная презентация), формулирование проблем, которые будут решаться в проекте;
Формирование групп для проведения исследований, распределение ролей участников групп;
Работа учащихся по поиску материалов к проекту, обработка информации;
Совместное обсуждение в группах результатов проекта.
Выполнение дидактических заданий к проекту:
Буклета Тела вращения;
Кроссвордов Тела вращения;
Теста Тела вращения.
Оформление результатов исследования в форме презентаций и рефератов.
Презентация результатов проекта на уроке-конференции.
Оценивание работы по проекту участниками, учителем.
Подведение итогов
Слайд 10Этапы проектной деятельности:
1. Организационный - выбор учащимися интересующего их вопроса,
2. Поисковый - сбор информации о данном вопросе.
3. Аналитический - анализ и систематизация, изучение полученного материала.
4. Этап оформления - составление проекта в программе Power Point.
5. Презентационный - выступление с проектом
Слайд 11Направления исследования.
Теоретики-математики (проблемные вопросы с научной точки зрения);
Историки (развитие теории
Практики (практическое применение теории в жизни).
Слайд 12Подготовка учащихся
к работе над проектом.
Формируются группы учащихся, где перед
Распределяются обязанности , с учетом склонности учащихся к рассуждениям, формулированию выводов, оформлению проектной работы.
Составляется план работы над проектом, проводится анализ имеющейся информации.
Слайд 13Выполнение проекта.
Этот этап включает в себя:
- самостоятельный поиск новой
- систематизация и анализ собранного материала;
- создание и оформление проекта.
Слайд 14Презентация проектов.
Весь подготовленный, оформленный материал надо представить одноклассникам, защитить свой
Слайд 15Подведение итогов проектной работы.
Вопросы для обсуждения:
Появились ли у вас
Что в работе над проектом было наиболее интересным?
Каковы были основные трудности и как вы их преодолевали?
Какие можете сделать себе замечания и предложения на будущее?
Слайд 16Творческие задания групп были выполнены следующим образом:
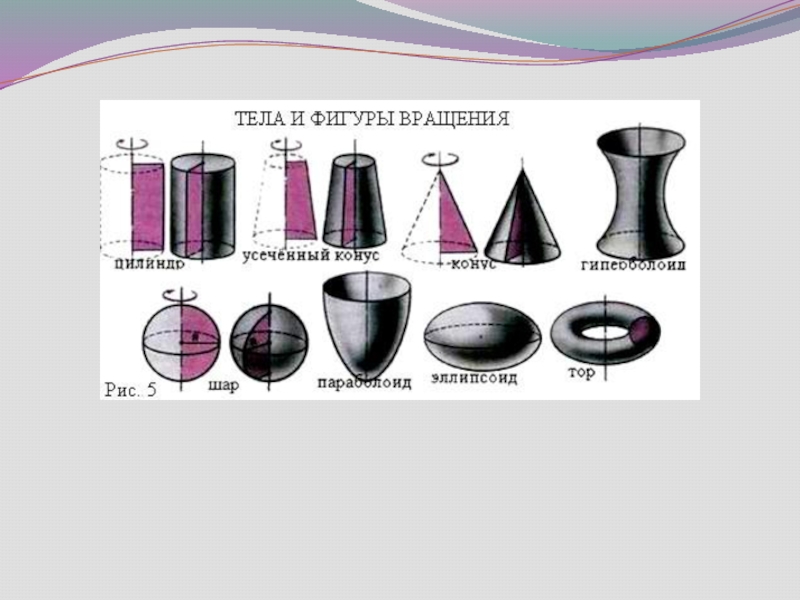
Группы "Теоретиков-математиков"
Цилиндр, Конус, Усеченный
Построение изображений тел вращения и их сечений (презентация)
Поверхности второго порядка (презентация)
Группы "Историков"
Первые сведения о телах вращения и их свойствах. Биографии ученых, внесших весомый вклад в развитие науки о телах вращения. Когда люди научились вычислять площади и объемы? (презентация)
Геометрические тайны Земли (презентация)
Группы "Практиков"
Тела вращения в быту и архитектуре (презентация)
Кроссворды и ребусы (презентация)
Дидактические материалы, тесты (электронное пособие)
Слайд 22Конус (моллюск)
Яд конуса (Conus magus) применяется как обезболивающее (анальгетик). Например препарат
одного из пептидов конуса, действие которого превосходит все известные медициной препараты. Этим ядом предполагается заменить вызывающие наркоманию морфины
Конусы очень высоко ценятся коллекционерами. Конус Глориамарис (Conus gloriamaris), называемый «Славой морей», считается самой красивой раковиной в мире. Описаная ещё в 1777 г. до 1950 г. было известно всего около двух десятков этих раковин и поэтому они могли стоить до нескольки тысяч долларов.
Конусы (лат. Conidae) — семейство хищных брюхоногих моллюсков. Своих жертв, в роли которых обычно выступают многощетинковые черви и моллюски (реже — ракообразные и рыбы), конусы парализуют с помощью яда. Описано около 500 видов. Большинство представителей приурочено к тёплым тропическим морям, однако некоторые способны обитать в высоких широтах.
Укус некоторых представителей рода Conus смертельно опасен для человека. В то же время, яд других видов используют в фармакологии для изготовления сильнодействующих обезболивающих препаратов, не вызывающих наркотической зависимости.
Слайд 24кроссворд "тела и фигуры вращения"
По горизонтали. 1. Фигура на плоскости, все
По вертикали. 1. Тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов. 2. Плоская фигура, при вращении которой образуется усечённый конус. 3. Тело вращения, являющееся верхней частью архитектурного сооружения. 4. Отрезок, соединяющий две точки сферы и проходящий через центр шара. 5. Тело, полученное вращением полукруга вокруг его диаметра. 6. Фигура, полученная вращением полуокружности вокруг её диаметра. 7. Тело вращения, об устойчивости движения которого написана известная работа великой русской женщины – математика.
Слайд 25Ответы к кроссворду .
К
У
П
Л
К Р У
Ш
Р
О
Н
С
Т
А
П
Е
И
П Р Я М О Й
Ц И Л И Н Д Р
Л
А
С
Ф
Е
А
Д
А
Е
Т
Т О Р
О Б Р А З У Ю Щ А Я
Слайд 26Тест
1 вариант
Диагональ осевого сечения цилиндра равна
Образующая конуса наклонена к плоскости основания под углом 300 и равна 8см. Найти площадь осевого сечения конуса. а)8 см2; б)16 см2; в)4 см2; г)16 см2.
Найти расстояние от центра шара до плоскости сечения, если радиус шара равен 6см, а радиус сечения равен 3 см. а)2 см; б)4см; в)3см; г)5см.
Радиусы оснований усеченного конуса равны 12см и 6см, образующая наклонена к плоскости основания под углом 450. Найти высоту конуса. а)3см; б)4см; в)6см; г)5см.
Правильная треугольная призма вписана в шар. Найти высоту призмы, если радиус шара 4см, а ребро основания призмы - 6см. а)2см; б)4см; в)8см; г)10см.
2 вариант
Площадь осевого сечения цилиндра равна 12см2, высота – 2см. Найти радиус основания. а)3 см; б)4см; в)5см; г)3см.
Образующая конуса наклонена к плоскости основания под углом 600 и равна 4см. Найти площадь осевого сечения конуса. а)8 см2; б)16 см2; в)4 см2; г) 8см2.
Найти радиус шара, если расстояние от центра шара до плоскости сечения равно 3см, радиус сечения равен см. а)2 см; б)4см; в)2,5см; г)3см.
Радиусы оснований усеченного конуса равны 10 см и 6 см, образующая наклонена к плоскости основания под углом 600. Найти высоту конуса. а)6см; б)3см; в)4см; г)12см.
Правильная четырехугольная призма вписана в шар. Найти высоту призмы, если радиус шара 6см, а ребро основания призмы - 5см.
а) 9см; б) 4 см; в) см; г)7см.
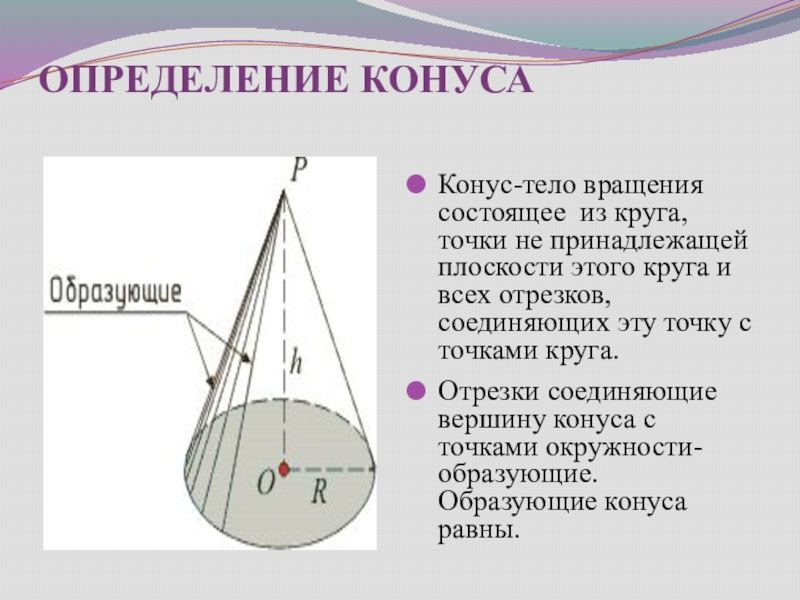
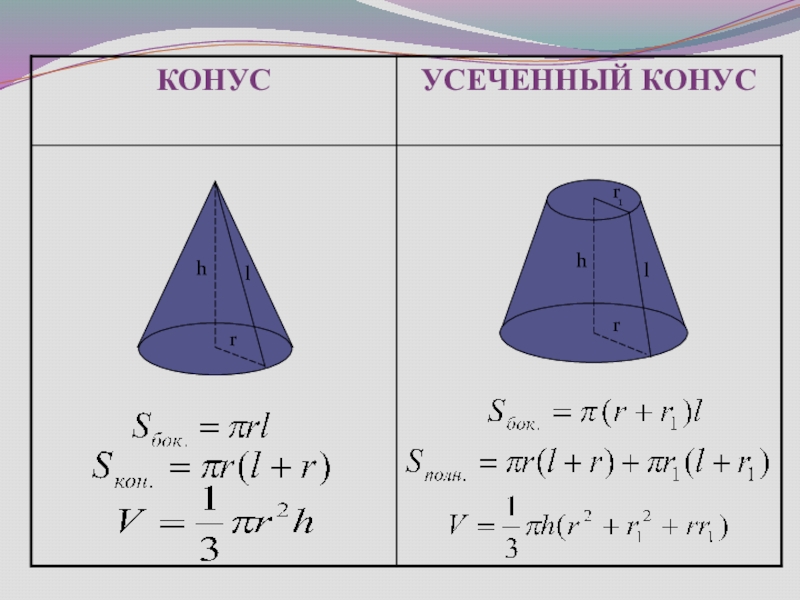
Слайд 29ОПРЕДЕЛЕНИЕ КОНУСА
Конус-тело вращения состоящее из круга, точки не принадлежащей плоскости этого
Отрезки соединяющие вершину конуса с точками окружности-образующие. Образующие конуса равны.
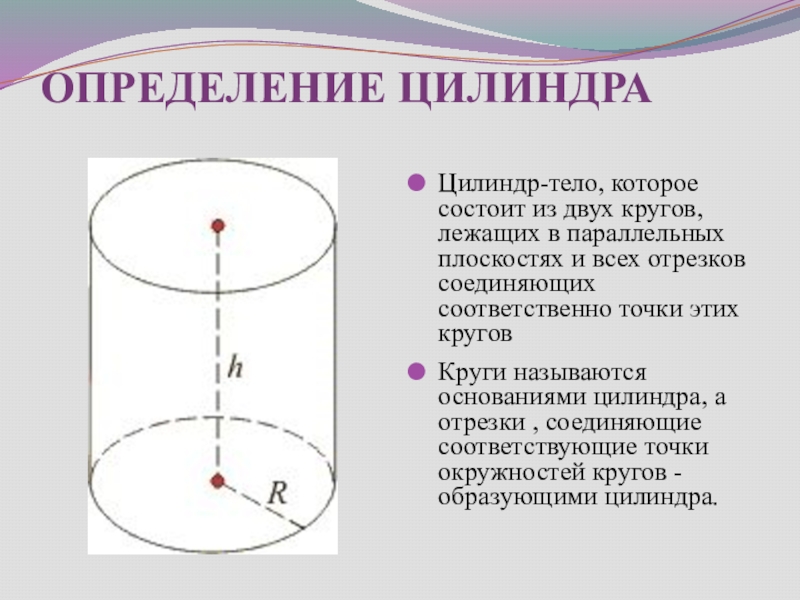
Слайд 30ОПРЕДЕЛЕНИЕ ЦИЛИНДРА
Цилиндр-тело, которое состоит из двух кругов, лежащих в параллельных плоскостях
Круги называются основаниями цилиндра, а отрезки , соединяющие соответствующие точки окружностей кругов -образующими цилиндра.
Слайд 31ОПРЕДЕЛЕНИЕ ШАРА
Шаром называется тело, которое состоит из всех точек пространства, находящихся
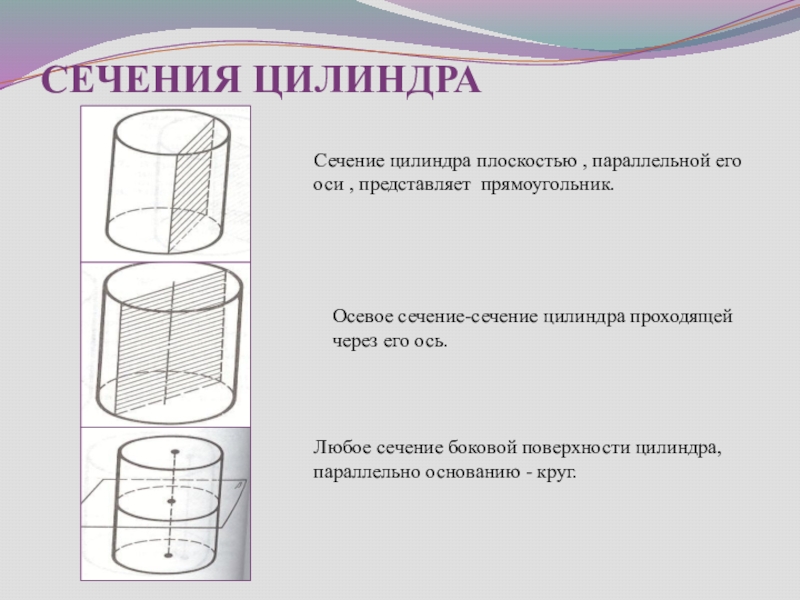
Слайд 34СЕЧЕНИЯ ЦИЛИНДРА
Сечение цилиндра плоскостью , параллельной его оси , представляет прямоугольник.
Осевое
Любое сечение боковой поверхности цилиндра, параллельно основанию - круг.
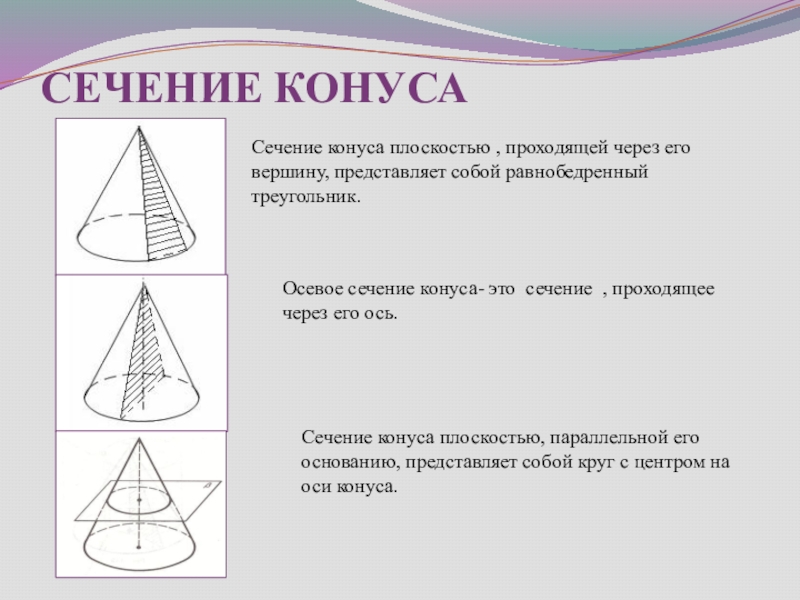
Слайд 35СЕЧЕНИЕ КОНУСА
Сечение конуса плоскостью , проходящей через его вершину, представляет собой
Осевое сечение конуса- это сечение , проходящее через его ось.
Сечение конуса плоскостью, параллельной его основанию, представляет собой круг с центром на оси конуса.
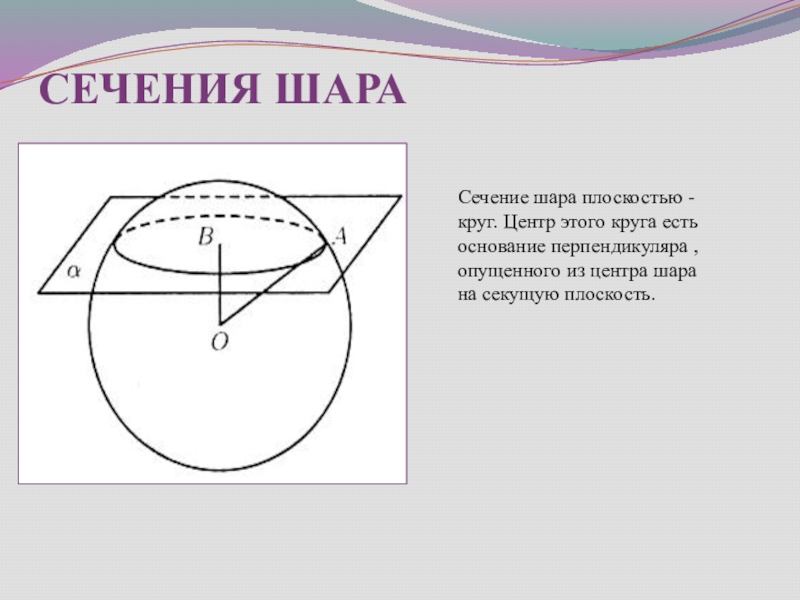
Слайд 36СЕЧЕНИЯ ШАРА
Сечение шара плоскостью -круг. Центр этого круга есть основание перпендикуляра
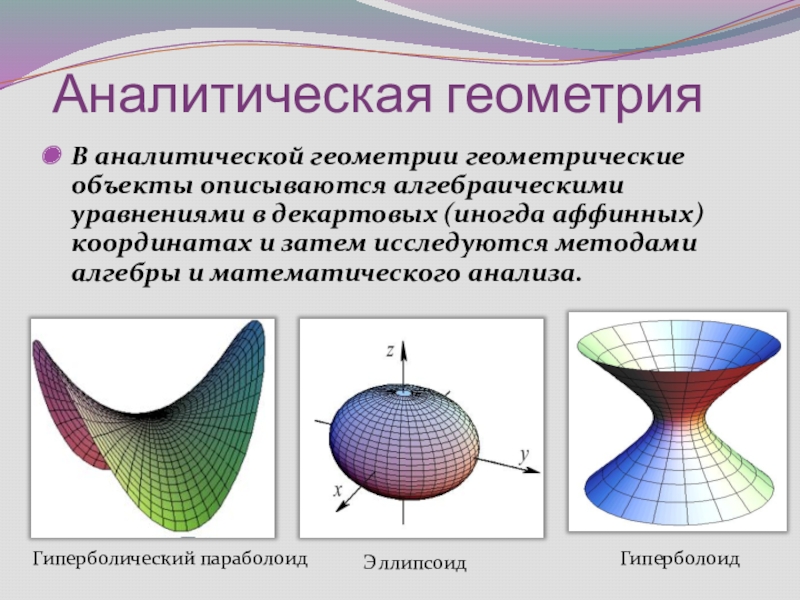
Слайд 38 Аналитическая геометрия
В аналитической геометрии геометрические объекты описываются алгебраическими уравнениями в
Гиперболический параболоид
Эллипсоид
Гиперболоид
Слайд 39Группы "Историков"
Московский математический папирус
Это один из древнейших известных современности математических текстов.
Слайд 40Задача № 10 Московского папируса
Связана с вычислением поверхности корзины с отверстием
Это первый в истории случай определения площади кривой поверхности, требующий использования числа π, которое египтяне определяли ≈ 3,16, тогда как на всём Древнем Ближнем Востоке оно считалось равным трём.
Слайд 41 Греч. (конос) --- конус, сосновая шишка, остроконечная верхушка шлема
У Евклида --- вращение прямоугольного треугольника вокруг катета.
У Аполлония --- движение образующей вдоль круговой направляющей. У Кавальери --- то же; в случае произвольной направляющей получается коника.
Л.Н.Бескин. Стереометрия.
Пособие для учителей средней школы
Евклид
Аполоний
Кавальери
Слайд 42Архиме́д
287 – 212 гг. до н.э.
Древнегреческий математик, физик, механик
Сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда важных изобретений.
*Сираку́зы — одна из первых греческих колоний на восточном берегу острова Сицилии.
Слайд 43Легенда об Архимеде
Архимед служил у царя Сиракуз Гиерона, служил верой
Однажды царь решил пожертвовать одному из храмов в Сиракузах золотую корону. Нашли лучшего мастера. Гиерон отпустил ему нужное количество золота.
Мастер потрудился на славу, и довольный царь расплатился с мастером за работу.
Корону взвесили, и ее вес оказался в точности равным весу отпущенного золота.
Вдруг поступил донос: “Царь, часть золота из короны украли, заменив серебром”.
Слайд 44Гиерон поручил Архимеду проверить честность мастера. Ученый думал… Думал дома, на
Погрузившись в ванну, Архимед вдруг заметил, что из ванны вытекает ровно такое количество воды, каков объем его тела, погруженного в воду.
Слайд 45 Корона вытеснила воды больше, чем слиток из золота. Кража золота
Согласно легенде, Архимед выскочил голый на улицу с криком «Эврика!», то есть «Нашёл!». В этот момент был открыт основной закон гидростатики: закон Архимеда.
Ученый изложил царю Гиерону свою идею: “Возьми, царь, два слитка — из золота и серебра — так, чтобы их вес был в точности равен весу короны, выполненной мастером. Затем в сосуд, заполненный до самых краев водой, будем опускать последовательно оба слитка и корону. Каждый раз будем измерять объем вытесненной воды”.
Слайд 47Неевклидовы геометрии
Сферическая геометрия — раздел геометрии, изучающий геометрические фигуры на поверхности сферы.
Слайд 48Процесс формирования планеты изначально начинается с появления какой-то материальной частицы. Она
Почему планеты имеют форму шара?
Слайд 49В психологических исследованиях рефлексия выступает двояко:
как способ осознания исследователем оснований и
как базовое свойство субъекта, благодаря которому становится возможным осознание и регуляция своей жизнедеятельности.
Почему планеты имеют форму шара?
Как получаются тела вращения?
Как изображают объемные тела вращения?
Что такое тело вращения?
Какие тела вращения вы знаете?
Как посчитать площади поверхности и объемы тел вращения?
Где мы можем увидеть тела вращения в быту и природе?
Как используют тела вращения в искусстве, архитектуре?
Итоговые вопросы (рефлексия):
Рефлексия (от лат. reflexio - обращение назад) – мыслительный процесс, направленный на самопознание, анализ своих эмоций и чувств, состояний, способностей, поведения.
Слайд 50Заключение
Основная задача проекта состоит не только в том, чтобы дать учащимся
Проектная деятельность формирует социальный опыт школьников в труде и общении, способствует их интеллектуальному росту, расширяет кругозор, как в области своего предмета, так и в окружающей действительности, даёт возможность лучше раскрыть собственный потенциал.
Проект ценен тем, что в ходе его выполнения, школьники учатся самостоятельно добывать знания, получают навыки ориентирования в потоке информации, учатся анализировать, обобщать, сопоставлять факты, делать выводы и заключения. У учащихся формируется научно - теоретическое, нестандартное мышление.
Метод проектов позволяет школьникам перейти от усвоения готовых знаний к их осознанному приобретению.
Слайд 51Выводы.
Реализация проектного и исследовательского методов на практике ведет к изменению позиции
Меняется и психологический климат на уроке. Из авторитетного источника информации преподаватель становится соучастником исследовательского, творческого процесса, наставником, консультантом, организатором самостоятельной деятельности учащихся. А это и есть подлинное сотрудничество.