- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Симметрия многогранников
Содержание
- 1. Презентация по геометрии Симметрия многогранников
- 2. Правильных многогранников вызывающе мало, но этот весьма
- 3. Симметрия относительно точкиСимметрия относительно прямойАОТочки А и
- 4. Симметрия относительно плоскостиАТочки А и А1 называются
- 5. Если фигура имеет центр (ось, плоскость) симметрии,
- 6. С симметрией мы часто встречаемся в архитектуре.
- 7. Правильные многогранники и природа
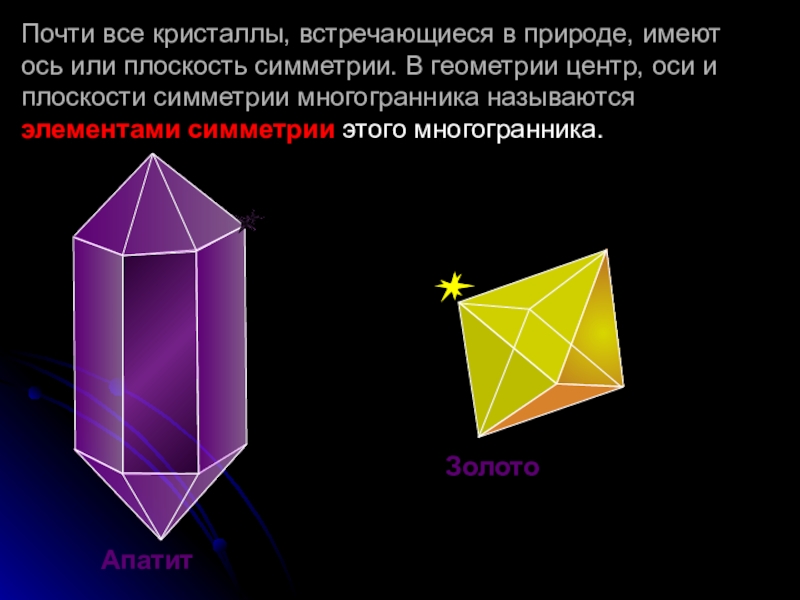
- 8. Почти все кристаллы, встречающиеся в природе, имеют
- 9. 4 грани, 4 вершины и 6 ребер.Сумма
- 10. Правильный тетраэдр не имеет центра симметрии. Осей
- 11. Правильный октаэдр составлен из восьми равносторонних треугольников.Каждая
- 12. «икоса» - 20Икосаэдр имеет 20 граней, 12 вершин и 30 ребер < 360°
- 13. Правильный додекаэдр составлен из двенадцати правильных шестиугольников.
- 14. Куб составлен из шести квадратов. Каждая вершина
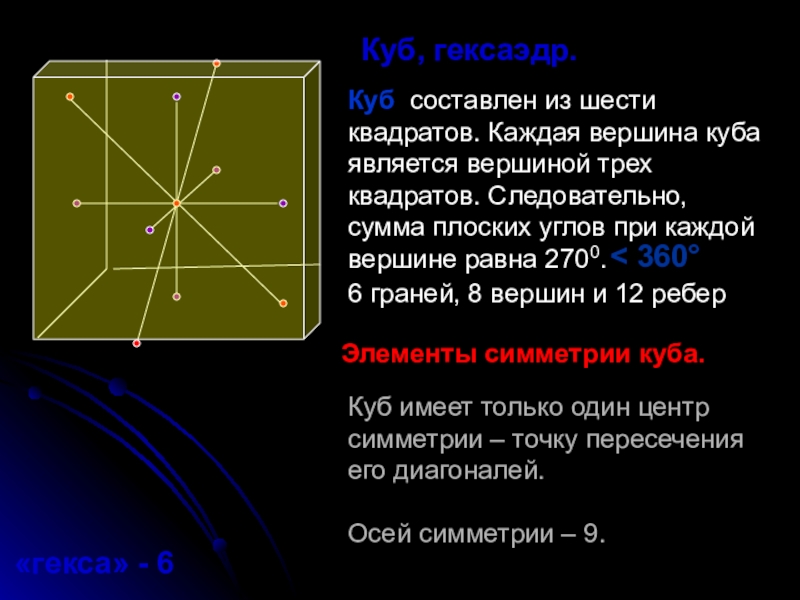
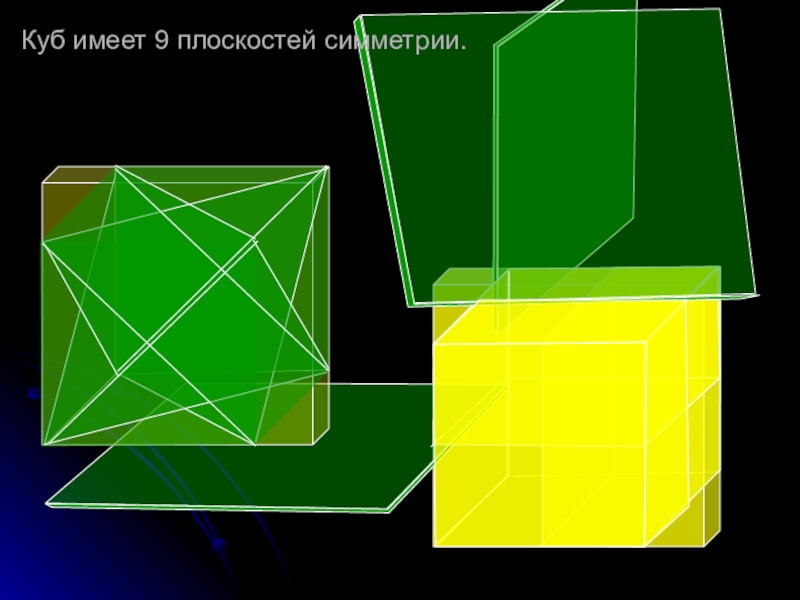
- 15. Куб имеет 9 плоскостей симметрии.
- 16. Названия многогранников пришли из Древней Грециив
- 17. Первым свойства правильных многогранников описал древнегреческий ученый
- 18. Правильные многогранники в философской картине мира ПЛАТОНА огоньвода
- 19. «Космический кубок» КеплераМодель Солнечной системы И. Кеплера
- 20. Икосаэдро-додекаэдровая структура Земли
- 21. Формула ЭйлераСумма числа граней и вершин любого
- 22. Слайд 22
- 23. Усеченный тетраэдрВыполняя простейшие сечения, мы можем получить
- 24. Усеченный кубСрезав вершины получим новые грани –
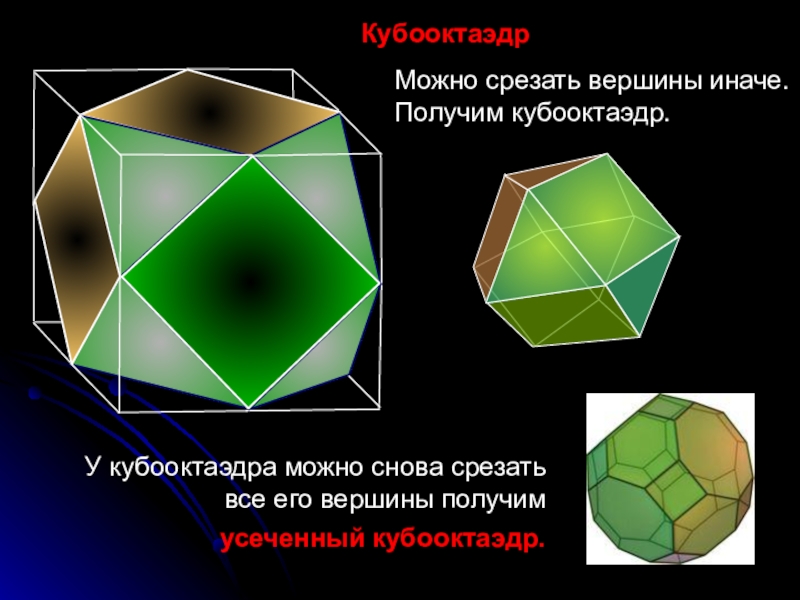
- 25. КубооктаэдрМожно срезать вершины иначе. Получим кубооктаэдр.
- 26. Усеченный октаэдрСрежем у октаэдра все его восемь
- 27. Можно срезать вершины иначе и получим новый полуправильный многогранник.
- 28. Срезав вершины икосаэдра, получим новые грани пятиугольники,
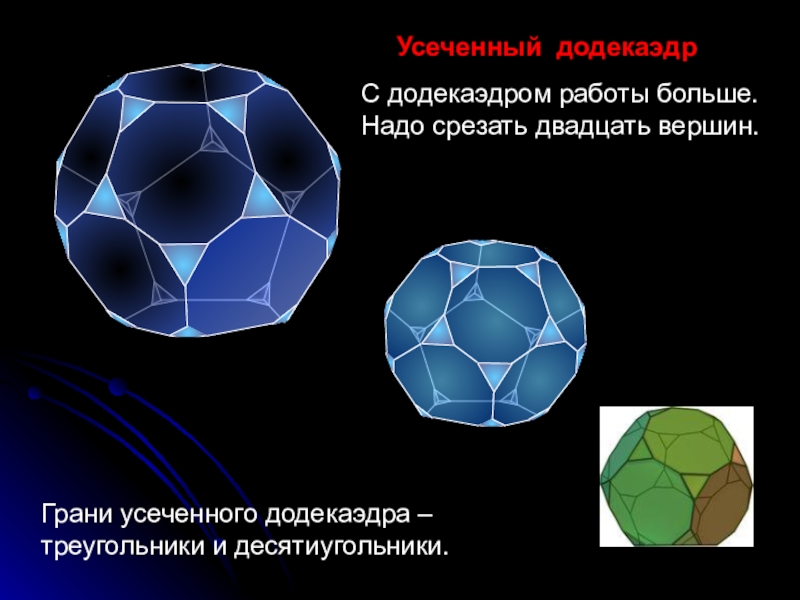
- 29. Усеченный додекаэдрС додекаэдром работы больше. Надо срезать двадцать вершин.Грани усеченного додекаэдра – треугольники и десятиугольники.
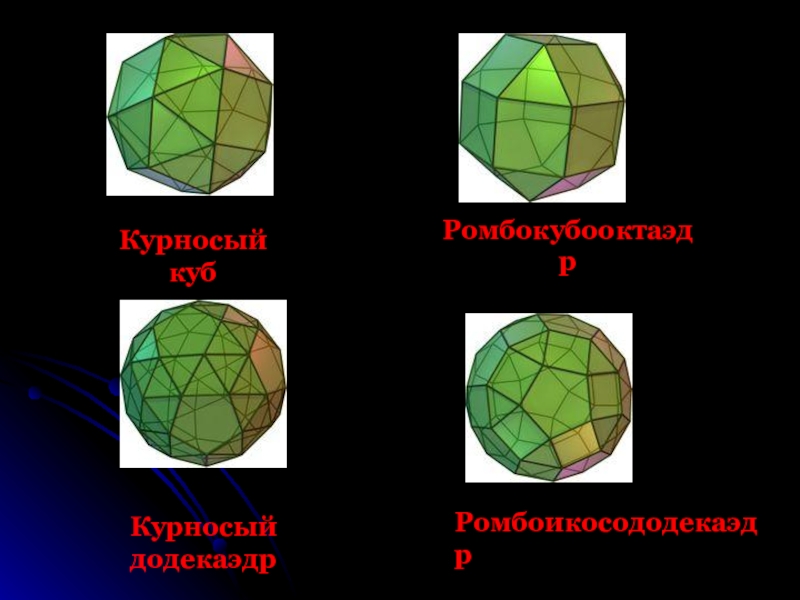
- 30. Курносый кубКурносый додекаэдр
Слайд 2 Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд
Л.Кэролл
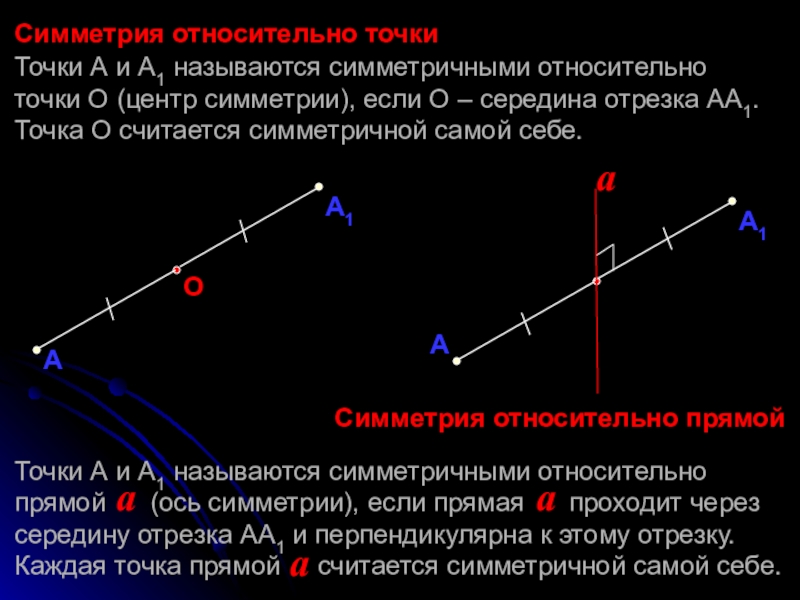
Слайд 3Симметрия относительно точки
Симметрия относительно прямой
А
О
Точки А и А1 называются симметричными относительно
Точка О считается симметричной самой себе.
Слайд 4
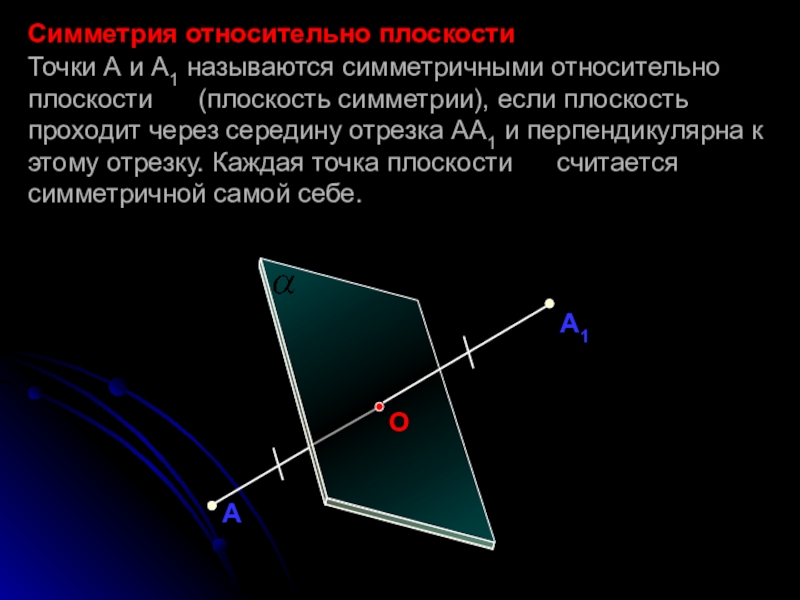
Симметрия относительно плоскости
А
Точки А и А1 называются симметричными относительно плоскости
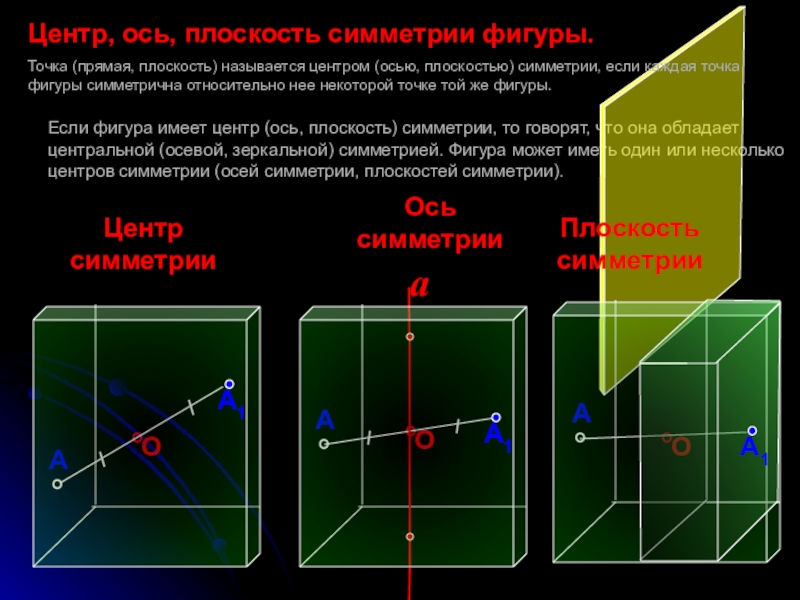
Слайд 5Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она
Центр
симметрии
Плоскость симметрии
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.
Центр, ось, плоскость симметрии фигуры.
Слайд 8Почти все кристаллы, встречающиеся в природе, имеют
ось или плоскость симметрии.
Золото
Слайд 94 грани, 4 вершины и 6 ребер.
Сумма плоских углов при каждой
Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится равное число ребер.
В каждом правильном многограннике сумма числа и вершин равна числу рёбер, увеличенному на 2.
60°+ 60° + 60° < 360°
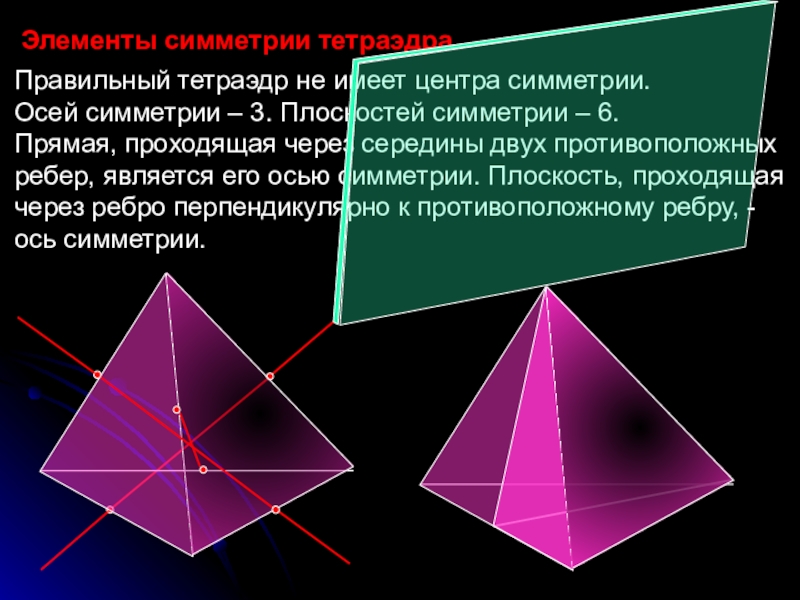
Слайд 10Правильный тетраэдр не имеет центра симметрии.
Осей симметрии – 3. Плоскостей
Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость, проходящая через ребро перпендикулярно к противоположному ребру, - ось симметрии.
Элементы симметрии тетраэдра.
Слайд 11
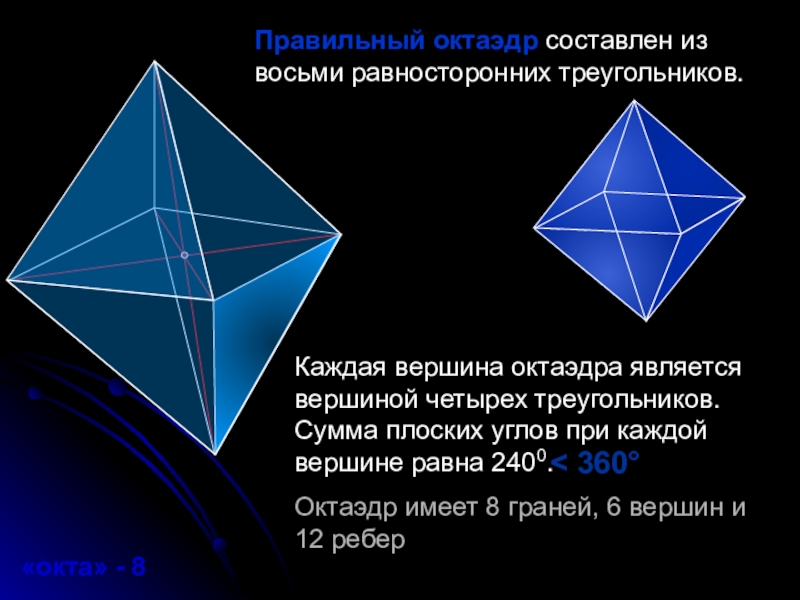
Правильный октаэдр составлен из восьми равносторонних треугольников.
Каждая вершина октаэдра является вершиной
«окта» - 8
Октаэдр имеет 8 граней, 6 вершин и
12 ребер
< 360°
Слайд 13Правильный додекаэдр составлен из двенадцати правильных шестиугольников. Каждая вершина додекаэдра является
«додека» - 12
Додекаэдр имеет 12 граней,
20 вершин и 30 ребер.
< 360°
Слайд 14Куб составлен из шести квадратов. Каждая вершина куба является вершиной трех
6 граней, 8 вершин и 12 ребер
«гекса» - 6
Куб, гексаэдр.
< 360°
Слайд 16Названия многогранников
пришли из Древней Греции
в них указывается число граней:
эдра −
тетра − 4
гекса − 6
окта − 8
икоса − 20
додека − 12
Слайд 17Первым свойства правильных многогранников описал древнегреческий ученый Платон. Именно поэтому правильные
Платон
428 – 348 г. до н.э.
Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Слайд 21Формула Эйлера
Сумма числа граней и вершин любого многогранника
равна числу рёбер,
Г + В = Р + 2
Число граней плюс число вершин минус число рёбер
в любом многограннике равно 2.
Г + В − Р = 2
Слайд 23
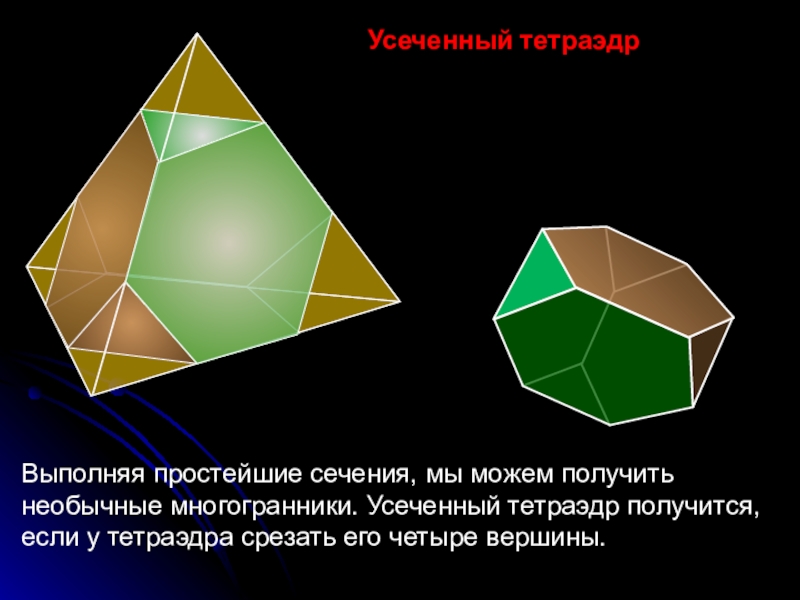
Усеченный тетраэдр
Выполняя простейшие сечения, мы можем получить необычные многогранники. Усеченный тетраэдр
Слайд 24
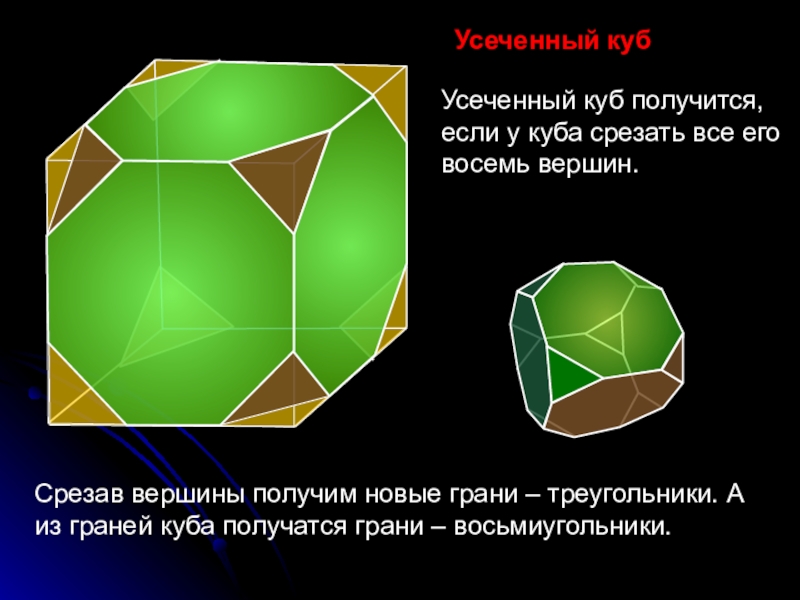
Усеченный куб
Срезав вершины получим новые грани – треугольники. А из граней
Усеченный куб получится, если у куба срезать все его восемь вершин.
Слайд 26
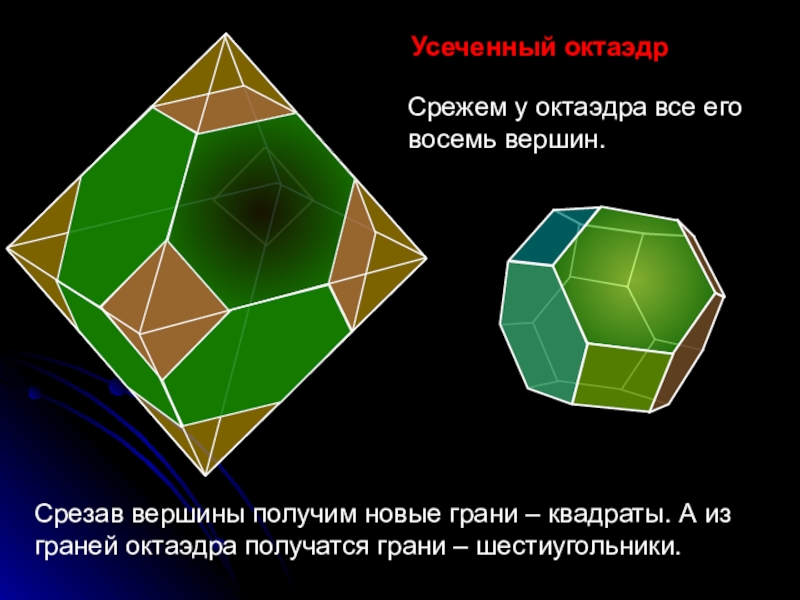
Усеченный октаэдр
Срежем у октаэдра все его восемь вершин.
Срезав вершины получим новые
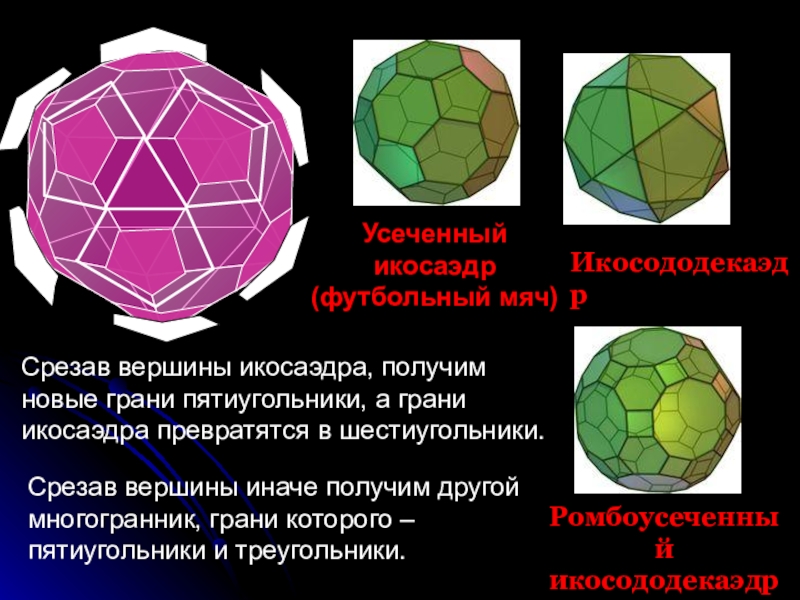
Слайд 28Срезав вершины икосаэдра, получим новые грани пятиугольники, а грани икосаэдра превратятся
Срезав вершины иначе получим другой многогранник, грани которого – пятиугольники и треугольники.
Слайд 29Усеченный додекаэдр
С додекаэдром работы больше. Надо срезать двадцать вершин.
Грани усеченного додекаэдра
