- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Решение задач повышенного уровня сложности по теме Окружность на ГИА
Содержание
- 1. Презентация по геометрии Решение задач повышенного уровня сложности по теме Окружность на ГИА
- 2. Цель занятий: Совершенствование умения решать геометрические задачи.
- 3. Если вы хотите научиться решать геометрические задачи,
- 4. Необходимо научиться именно решать задачи, а не
- 5. В известной книге Дьёрдь По́йа «Как решать
- 6. Можно дополнительно дать еще такие советы.1).Пусть при
- 7. На сегодняшнем занятии мы будем решать задачи
- 8. Итак, наша первая задача:№ 1. Медиана BM треугольника ABC равна 3 и
- 9. Обзор теоретического материала по тексту задачи:1) Медиана
- 10. 3) Вписанный угол, опирающийся на диаметр –
- 11. Определение: Окружностью называется геометрическая фигура, состоящая из
- 12. № 1. Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей
- 13. № 1. Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC. АВОМКС
- 14. Итак, взгляд назад. Повторим этапы решения задачи
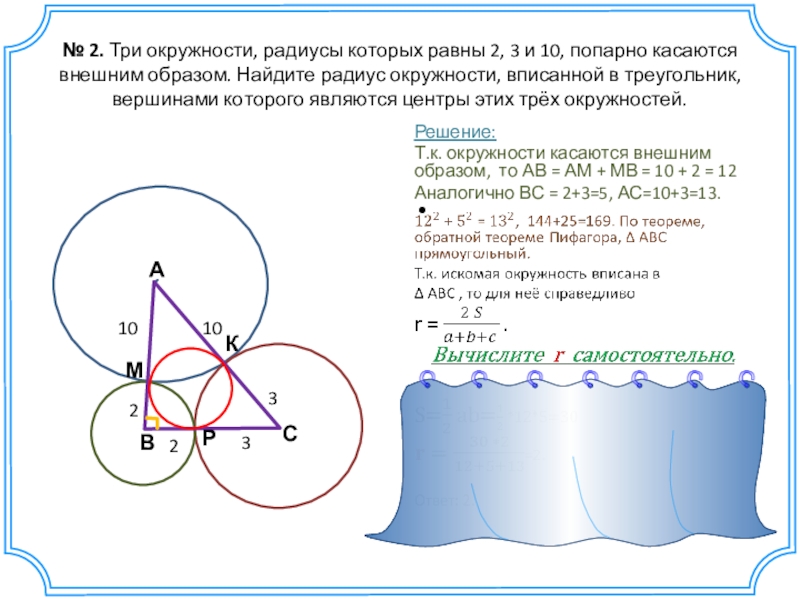
- 15. № 2. Три окружности, радиусы которых равны 2, 3
- 16. Теорема, обратная теореме Пифагора: Если в треугольнике
- 17. Вписанная в произвольный треугольник окружностьabc
- 18. № 2. Три окружности, радиусы которых равны 2, 3
- 19. № 2. Три окружности, радиусы которых равны 2, 3
- 20. Итак, повторим план решения задачи:АВСсba
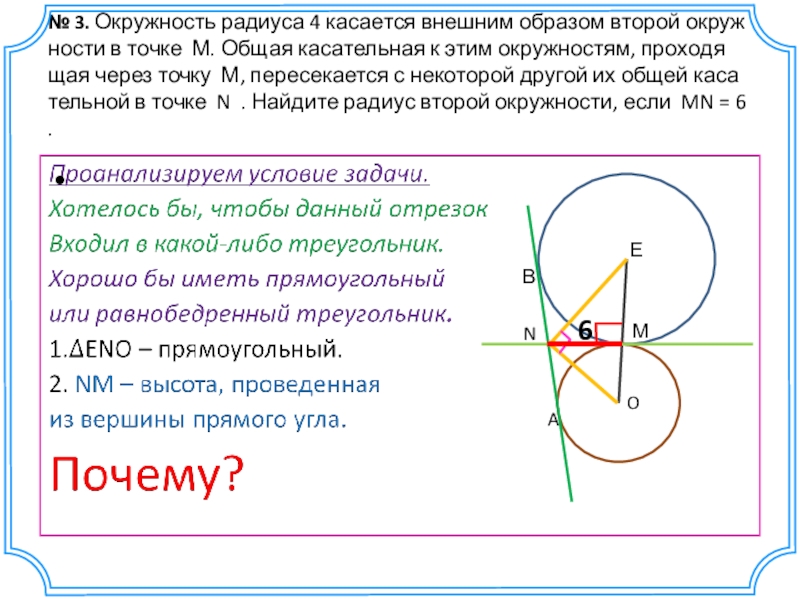
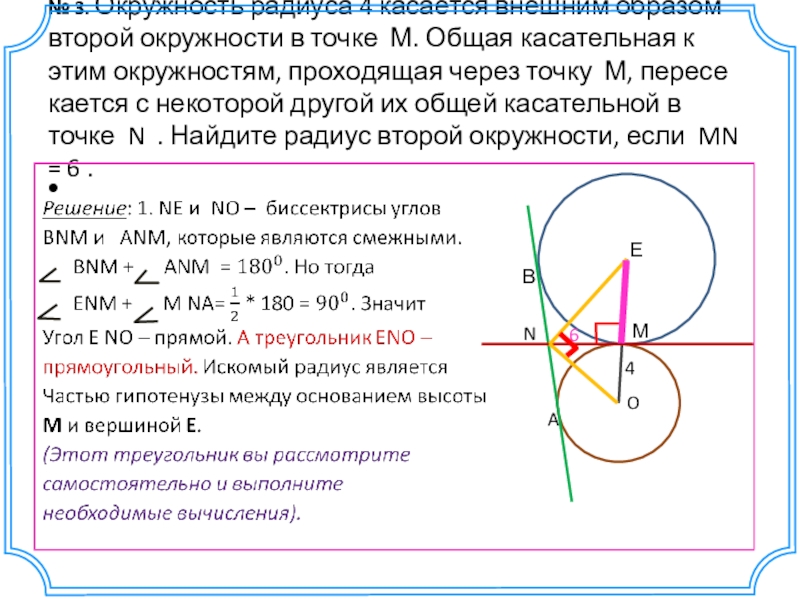
- 21. № 3. Окружность радиуса 4 касается внешним образом второй
- 22. № 3. Окружность радиуса 4 касается внешним образом второй
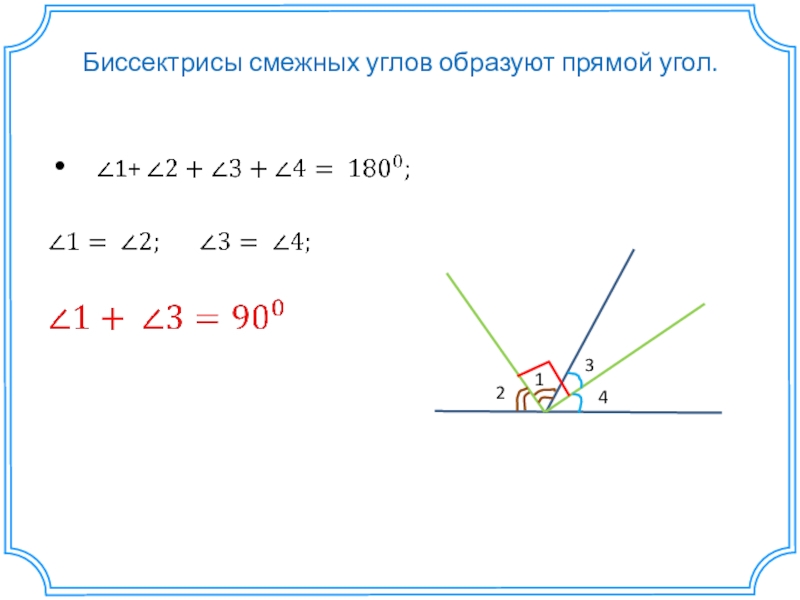
- 23. Биссектрисы смежных углов образуют прямой угол.1234
- 24. Если окружность вписана в угол, то ее
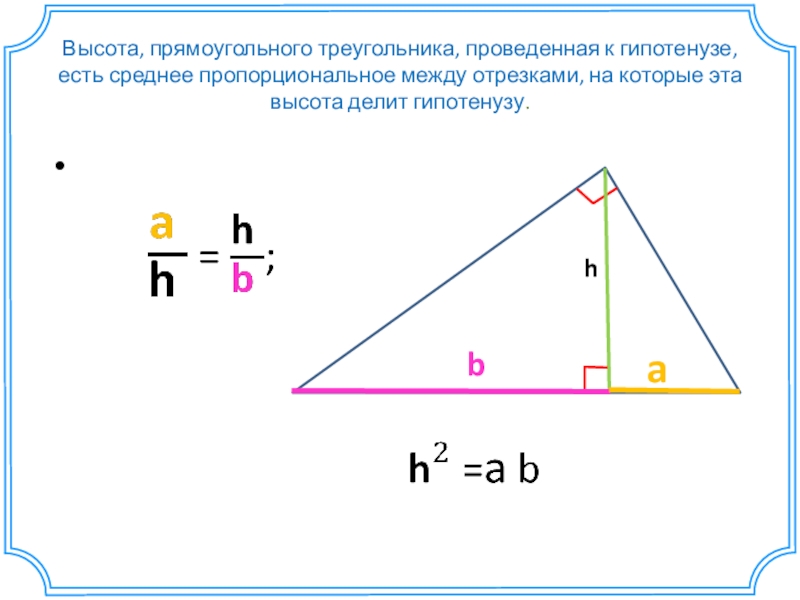
- 25. Высота, прямоугольного треугольника, проведенная к гипотенузе, есть
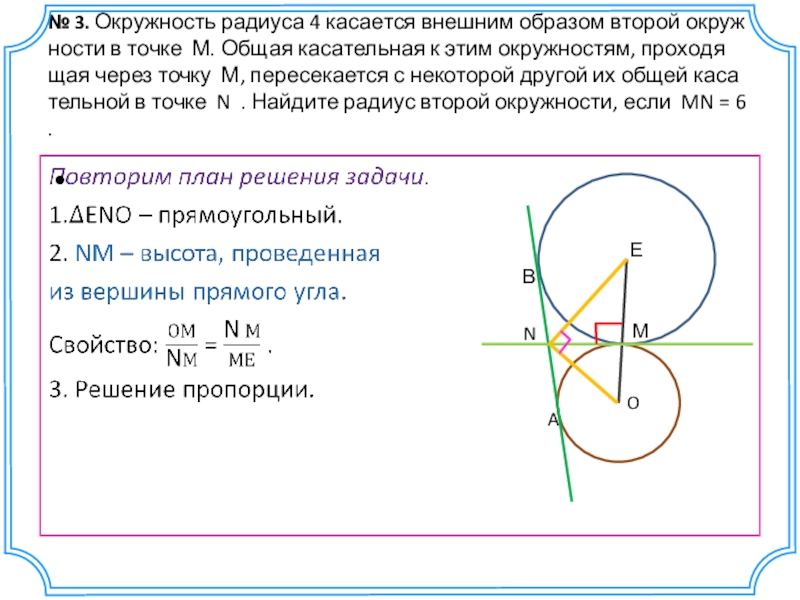
- 26. № 3. Окружность радиуса 4 касается внешним образом
- 27. Высота, прямоугольного треугольника, проведенная к гипотенузе, есть
- 28. № 3. Окружность радиуса 4 касается внешним образом второй
- 29. Спасибо за внимание!
- 30. В презентации использованы материалы сайта ФИПИ:http://opengia.ru/subjects/mathematics-9/topics/7.
- 31. источник шаблона: сайт http://pedsovet.su
Слайд 1Решение задач
повышенного уровня сложности
по теме «Окружность» на ГИА.
Учитель математики
Г. Курчатова
Курской области
Татаринова
Людмила Николаевна.
Слайд 2Цель занятий: Совершенствование умения решать геометрические задачи. Подготовка к ГИА.
Умение решать задачи… Искусство решать задачи… От чего оно зависит?
Каждый из вас изучал много определений, аксиом, теорем о свойствах и признаках различных геометрических фигур. Так какие из них нужно отыскать в памяти при решении конкретной задачи? Какие действия следует выполнить, чтобы задача была решена? Сложность геометрических задач в том и состоит, что нет четких алгоритмов их решения. Кроме того, многие задачи могут быть решены разными способами.
Слайд 3Если вы хотите научиться решать геометрические задачи, то прежде всего необходимо
Слайд 4Необходимо научиться именно решать задачи, а не запоминать их решение.
Известны такие
«Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!» Д. Пойа.
«Недостаточно лишь понять задачу, необходимо желание решить её. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдётся путь!» Д. Пойа
Слайд 5В известной книге Дьёрдь По́йа «Как решать задачу» автор предлагает следующий
Нужно ясно понять задачу. Что дано? Что неизвестно? В чем состоит условие? Сделайте чертеж. Введите необходимые обозначения.
Составьте план решения. Подумайте все ли данные вами использованы? Приняты ли во внимание все существенные понятия, содержащиеся в задаче?
Осуществите план решения, контролируя каждый шаг, обосновывая каждый шаг, ссылаясь на известные определения, аксиомы, теоремы.
Взгляд назад. Нужно изучить найденное решение.
Слайд 6Можно дополнительно дать еще такие советы.
1).Пусть при решении задачи вы пришли
2).Если при решении задачи вы используете треугольник, то следует попытаться выяснить, не является ли он прямоугольным, равнобедренным или равносторонним.
Слайд 7На сегодняшнем занятии мы будем решать задачи типа №26 ГИА, взятые
Четких алгоритмов решения этих задач нет, но в некоторых задачах рассматривается повторяющаяся конфигурация. В процессе решения мы заодно будем повторять школьный курс планиметрии.
Прочитав текст задачи, мы проанализируем ее и вспомним встретившиеся в условии понятия, свойства и признаки, которые будут использованы при решении данной задачи, а затем приступим к решению.
Очень полезно составлять план решения. Следует проследить за цепочкой рассуждений, которая может привести к успеху.
Слайд 8Итак, наша первая задача:
№ 1. Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей
Прежде, чем приступать к решению задачи, вспомним определения, свойства и признаки, которые нам понадобятся.
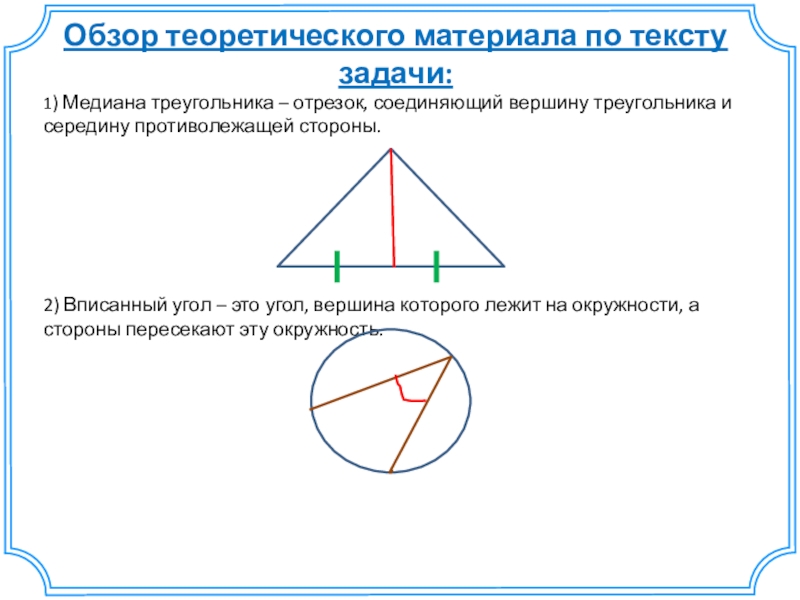
Слайд 9Обзор теоретического материала по тексту задачи:
1) Медиана треугольника – отрезок, соединяющий
2) Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
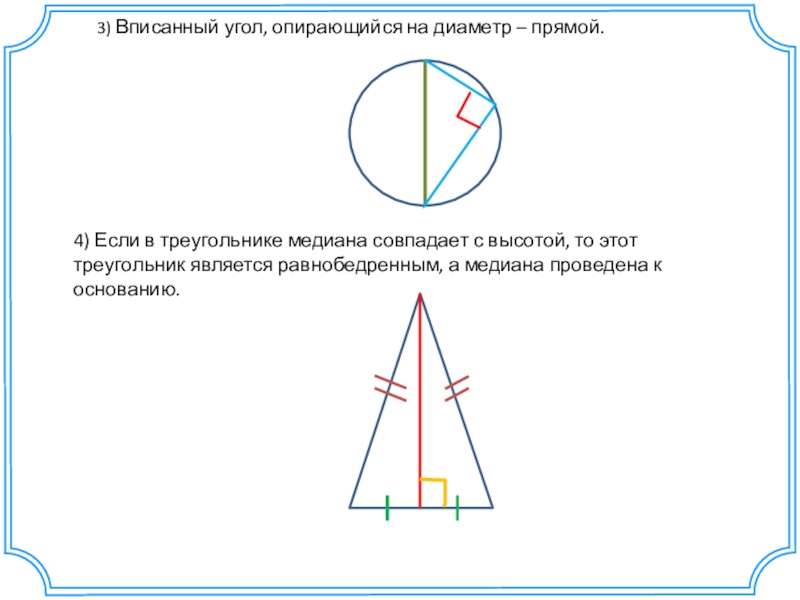
Слайд 103) Вписанный угол, опирающийся на диаметр – прямой.
4) Если в треугольнике
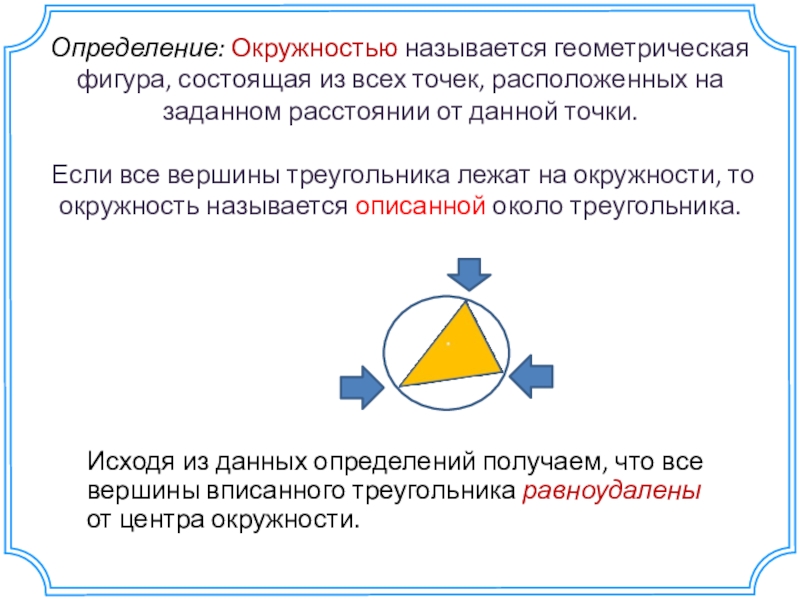
Слайд 11Определение: Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на
Исходя из данных определений получаем, что все вершины вписанного треугольника равноудалены от центра окружности.
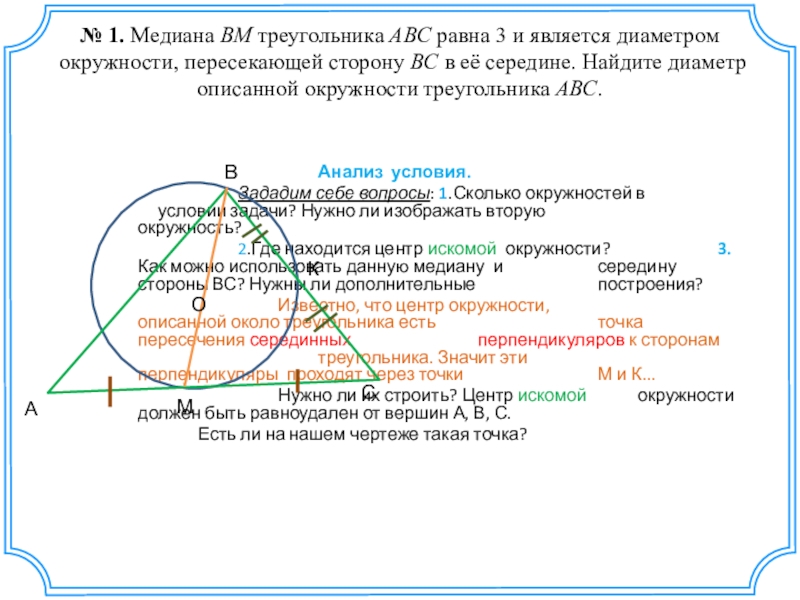
Слайд 12№ 1. Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите
Анализ условия.
Зададим себе вопросы: 1.Сколько окружностей в условии задачи? Нужно ли изображать вторую окружность?
2.Где находится центр искомой окружности? 3. Как можно использовать данную медиану и середину стороны ВС? Нужны ли дополнительные построения?
Известно, что центр окружности, описанной около треугольника есть точка пересечения серединных перпендикуляров к сторонам треугольника. Значит эти перпендикуляры проходят через точки М и К...
Нужно ли их строить? Центр искомой окружности должен быть равноудален от вершин А, В, С.
Есть ли на нашем чертеже такая точка?
А
В
О
М
К
С
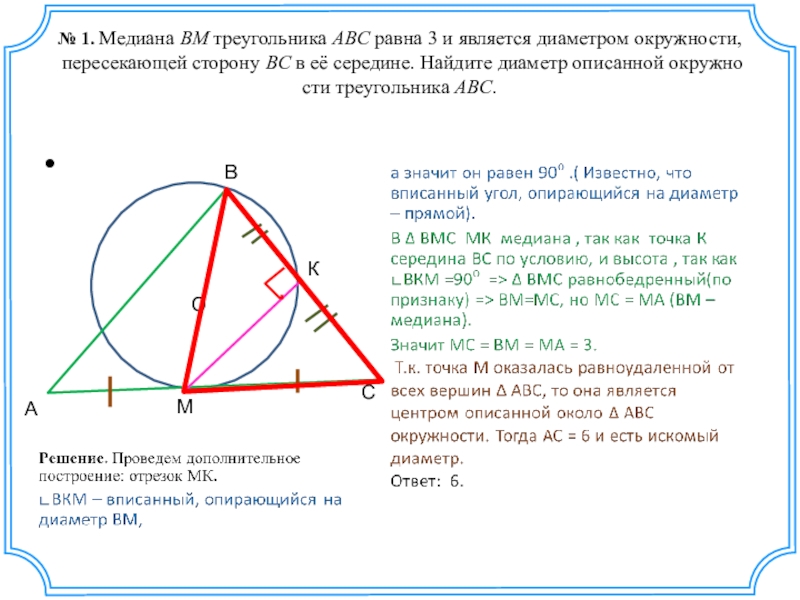
Слайд 13№ 1. Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите
А
В
О
М
К
С
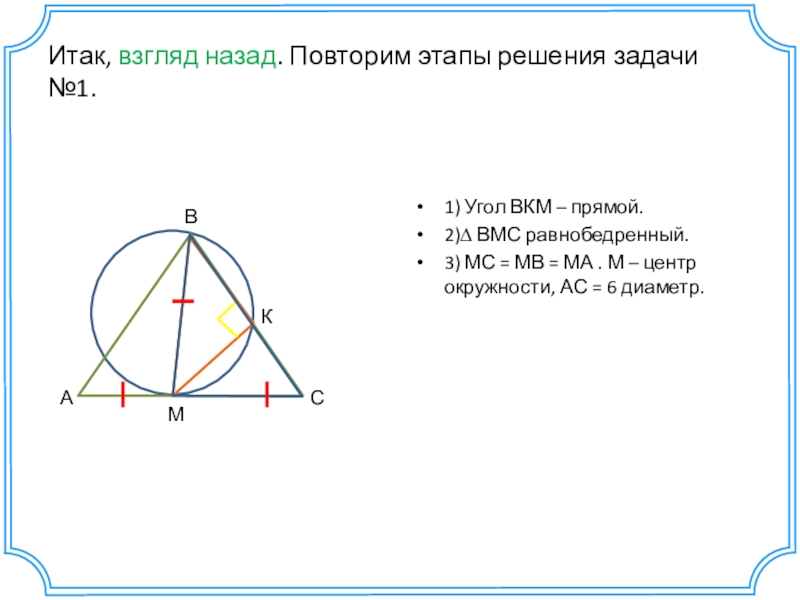
Слайд 14Итак, взгляд назад. Повторим этапы решения задачи №1.
1) Угол ВКМ –
2)∆ ВМС равнобедренный.
3) МС = МВ = МА . М – центр окружности, АС = 6 диаметр.
А
В
С
М
К
Слайд 15 № 2. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются
Обзор теоретического материала, необходимого при решении этой задачи.
Проанализируем условие задачи и
вспомним необходимые
для ее решения свойства
и признаки.
Внешнее касание окружностей.
1. Точки А, В, С лежат на одной прямой.
2. АС = R + r.
А
В
С
R
r
Слайд 16Теорема, обратная теореме Пифагора: Если в треугольнике квадрат одной стороны равен
а
b
с
А
В
С
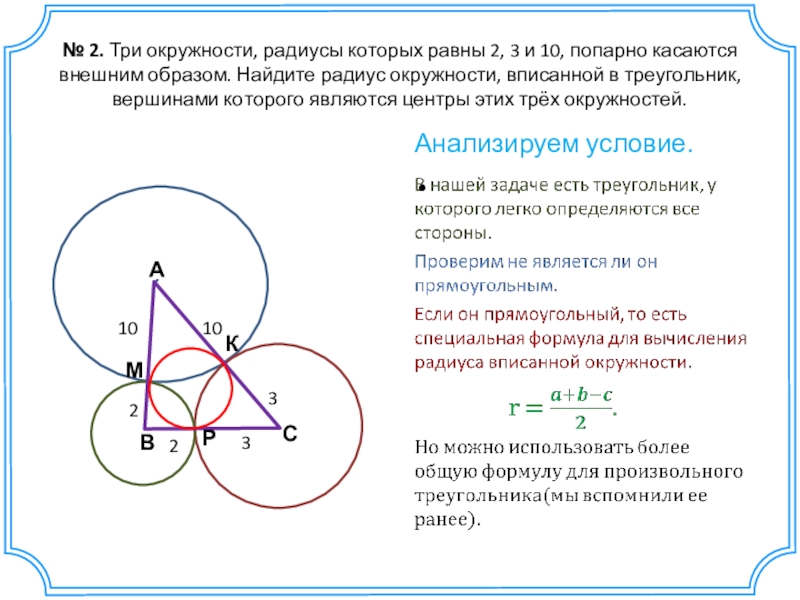
Слайд 18№ 2. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются
Анализируем условие.
А
В
С
М
К
Р
10
2
2
3
3
10
Слайд 19№ 2. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются
Решение:
Т.к. окружности касаются внешним образом, то АВ = АМ + МВ = 10 + 2 = 12
Аналогично ВС = 2+3=5, АС=10+3=13.
А
В
С
М
К
Р
10
2
2
3
3
10
Слайд 21№ 3. Окружность радиуса 4 касается внешним образом второй окружности в точке М.
В
Е
М
N
O
A
6
Слайд 22№ 3. Окружность радиуса 4 касается внешним образом второй окружности в точке М.
Обзор теоретического материала.
Внешнее касание:
1.Три общие касательные: MN, AB, m.
2. Радиусы , проведенные в точку касания
перпендикулярны касательной.
3. MN перпендикулярна ОЕ.
4. Изображая касательные, не забывайте
Отмечать прямые углы и равные отрезки.
5. AN = NB = NM по свойству отрезков
касательных.
А
В
N
M
O
E
m
Слайд 24Если окружность вписана в угол, то ее центр лежит на биссектрисе
АВ и АС касательные к окружности.
Отрезки касательных из одной точки
К одной окружности равны.
АВ = АС.
О
В
А
С
Слайд 25Высота, прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между отрезками,
h
b
a
Слайд 26 № 3. Окружность радиуса 4 касается внешним образом второй окружности в точке М.
В
Е
М
N
O
A
4
6
Слайд 27Высота, прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между отрезками,
N
О
М
Е
6
4
х
Слайд 28№ 3. Окружность радиуса 4 касается внешним образом второй окружности в точке М.
В
Е
М
N
O
A