- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Решение задач по теме Четырёхугольники
Содержание
- 1. Презентация по геометрии Решение задач по теме Четырёхугольники
- 2. Классная работа. Решение задач по теме «Четырёхугольники» Домашнее задание: инд. карточки.
- 3. Цели урока:Повторить, обобщить и систематизировать знания по данной теме.Сформировать навык применения изученных свойств при решении задач.
- 4. Слайд 4
- 5. Параллелограмм Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельныАВ ІІ DC, АD ІІ BCАDСВ
- 6. В параллелограмме противоположные стороны равны и противоположные углы равныAB = DC, BC = AD
- 7. Диагонали параллелограмма точкой пересечения делятся пополамAO =
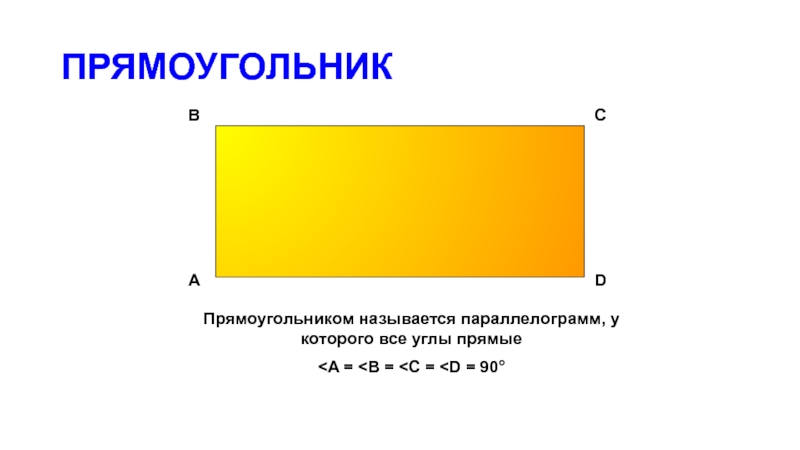
- 8. ПРЯМОУГОЛЬНИКПрямоугольником называется параллелограмм, у которого все углы прямые
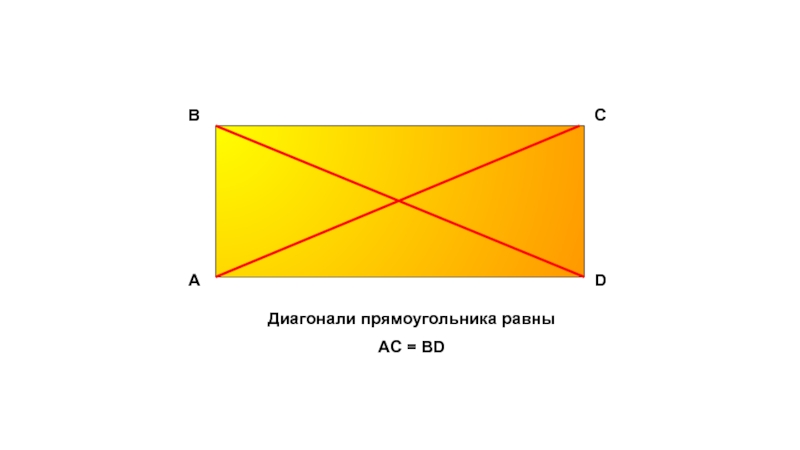
- 9. Диагонали прямоугольника равныAC = BDАDCB
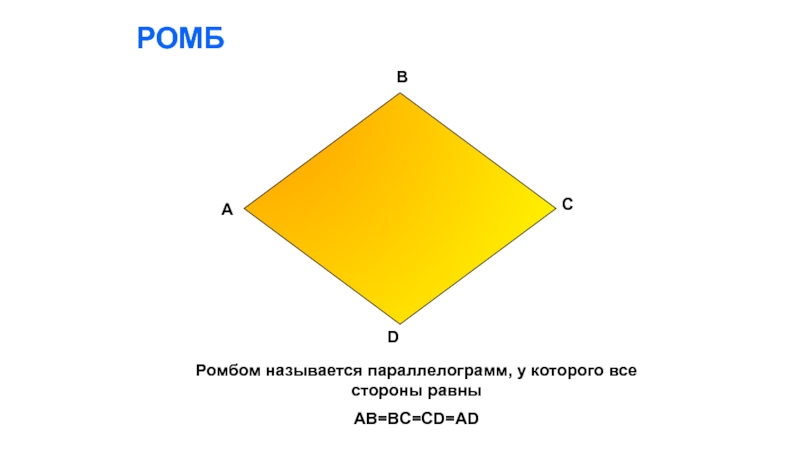
- 10. РОМБРомбом называется параллелограмм, у которого все стороны равныAB=BC=CD=ADADCB
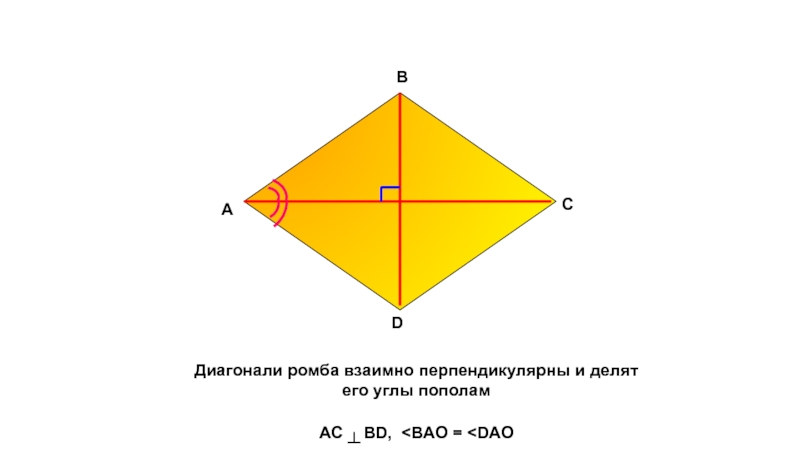
- 11. Диагонали ромба взаимно перпендикулярны и делят его углы пополамAC ┴ BD,
- 12. КвадратКвадратом называется прямоугольник, у которого все стороны равныAB = BC = CD = ADАDСВ
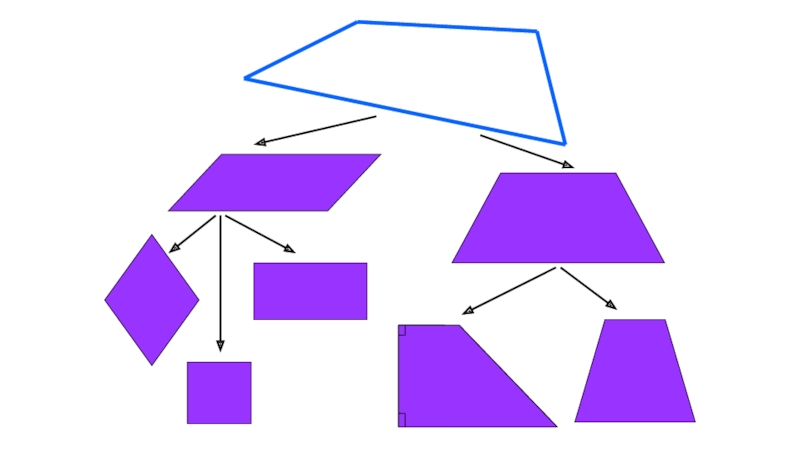
- 13. ТрапецияDСВАТрапецией называется четырёхугольник, у которого две стороны
- 14. АDСВТрапеция называется равнобедренной, если ее боковые стороны
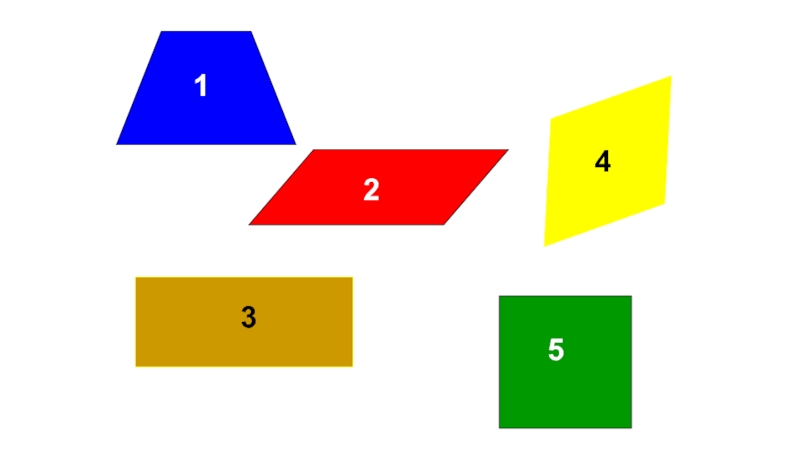
- 15. 12345
- 16. ВС
- 17. Слайд 17
- 18. Сейчас вам предстоит заполнить таблицу, отметив знаками
- 19. Слайд 19
- 20. Паркетчик вырезал квадраты из дерева и проверял
- 21. Решение задачЗадача 1.Меньшая сторона прямоугольника равна 4
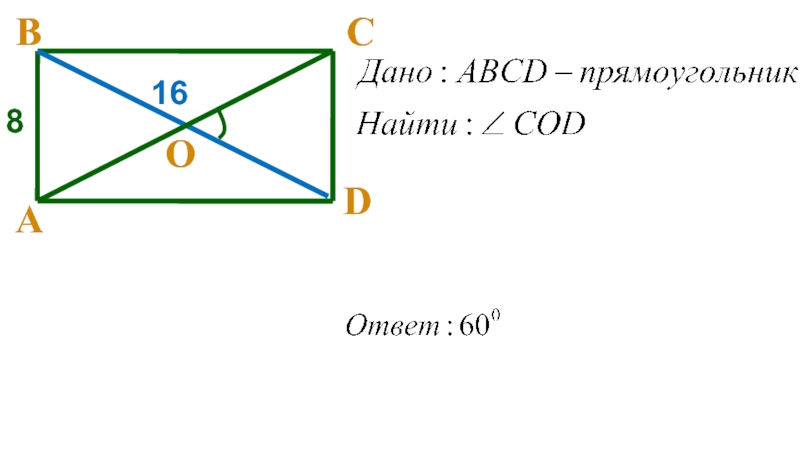
- 22. Дано: ABCD - прямоугольник,АВ = 4см,
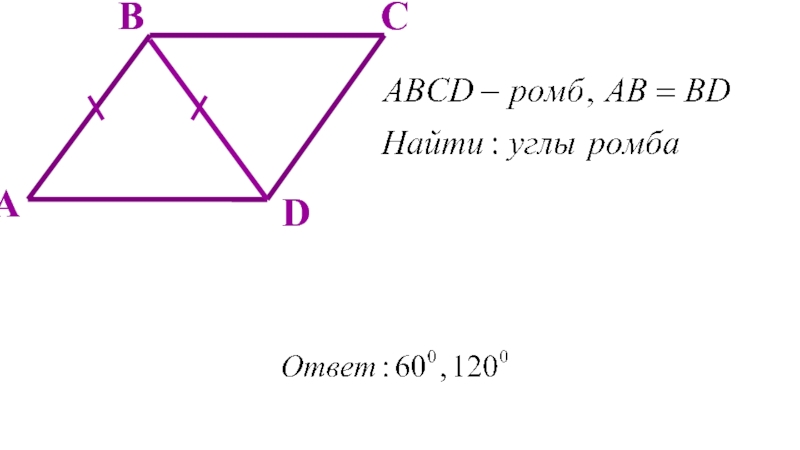
- 23. Дано:ABCD – параллелограмм,
- 24. Дано:ABCD- ромб,
- 25. № 407 (геометрия 7-9 кл. Атанасян и
- 26. Спасибо за урок!До свидания.
- 27. Использованная литература:Геометрия 7-9 кл, Атанасян и др;Журнал «Математика в школе»
Классная работа. Решение задач по теме «Четырёхугольники» Домашнее задание: инд. карточки.
Слайд 3Цели урока:
Повторить, обобщить и систематизировать знания по данной теме.
Сформировать навык применения
изученных свойств при решении задач.
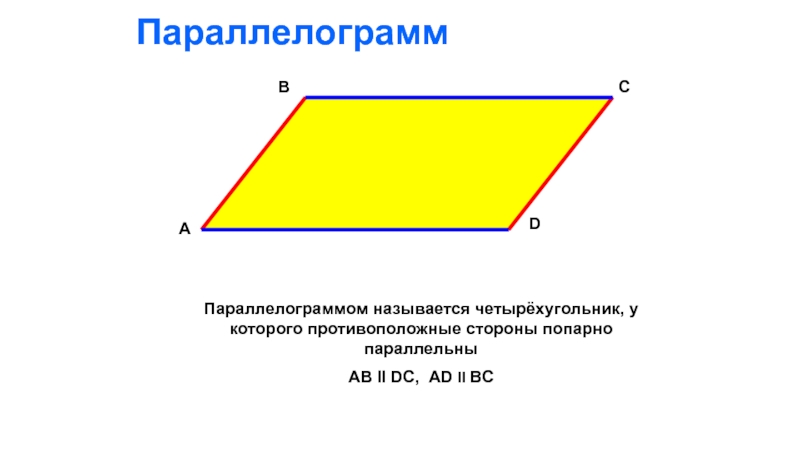
Слайд 5Параллелограмм
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны
АВ ІІ
DC, АD ІІ BC
А
D
С
В
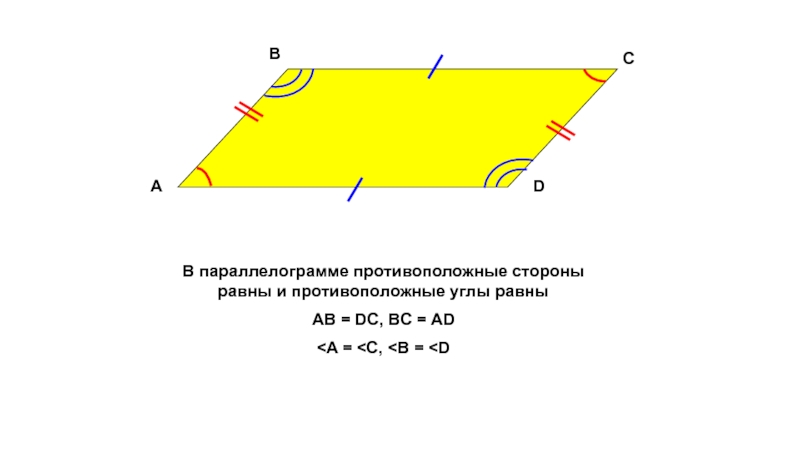
Слайд 6В параллелограмме противоположные стороны равны и противоположные углы равны
AB = DC,
BC = AD
B
A
D
C
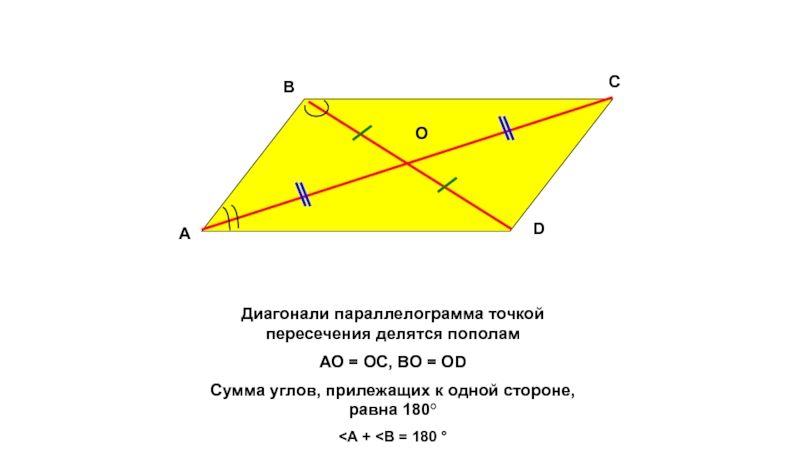
Слайд 7Диагонали параллелограмма точкой пересечения делятся пополам
AO = OC, BO = OD
Сумма
углов, прилежащих к одной стороне, равна 180°
<А + <В = 180 °
<А + <В = 180 °
A
D
C
B
O
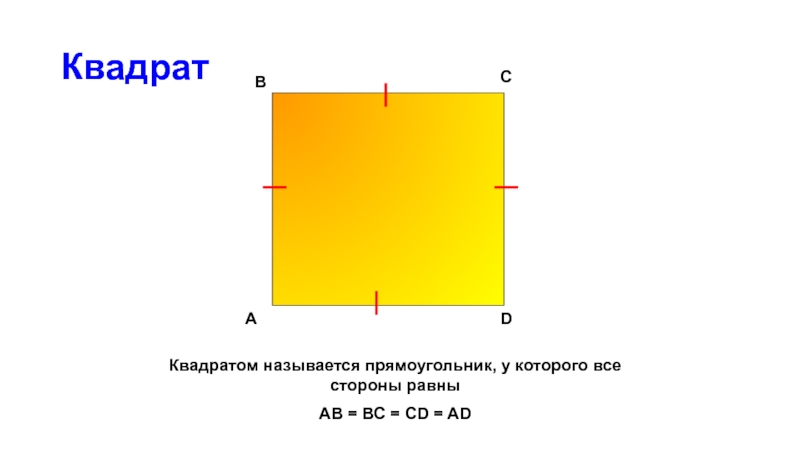
Слайд 12Квадрат
Квадратом называется прямоугольник, у которого все стороны равны
AB = BC =
CD = AD
А
D
С
В
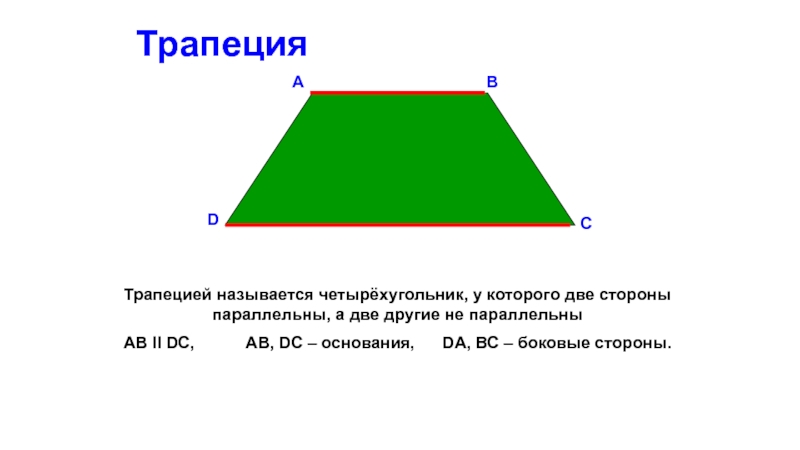
Слайд 13Трапеция
D
С
В
А
Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие
не параллельны
АВ ІІ DC, АВ, DC – основания, DА, ВС – боковые стороны.
АВ ІІ DC, АВ, DC – основания, DА, ВС – боковые стороны.
Слайд 14А
D
С
В
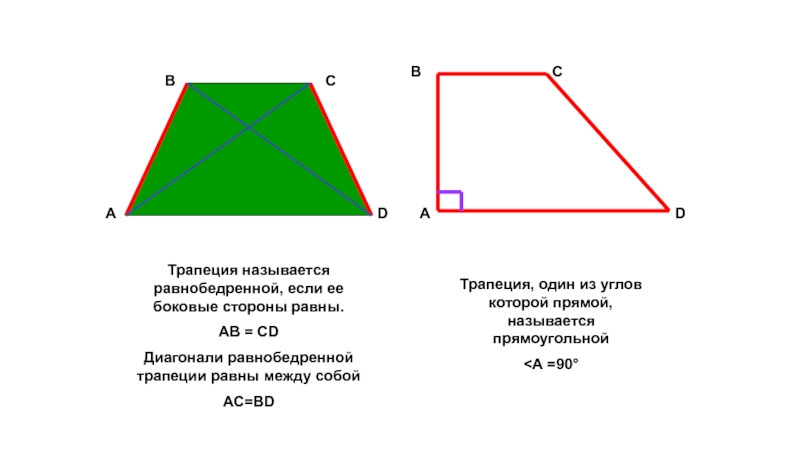
Трапеция называется равнобедренной, если ее боковые стороны равны.
АВ = СD
Диагонали равнобедренной
трапеции равны между собой
АС=BD
АС=BD
Трапеция, один из углов которой прямой, называется прямоугольной
<А =90°
А
В
С
D
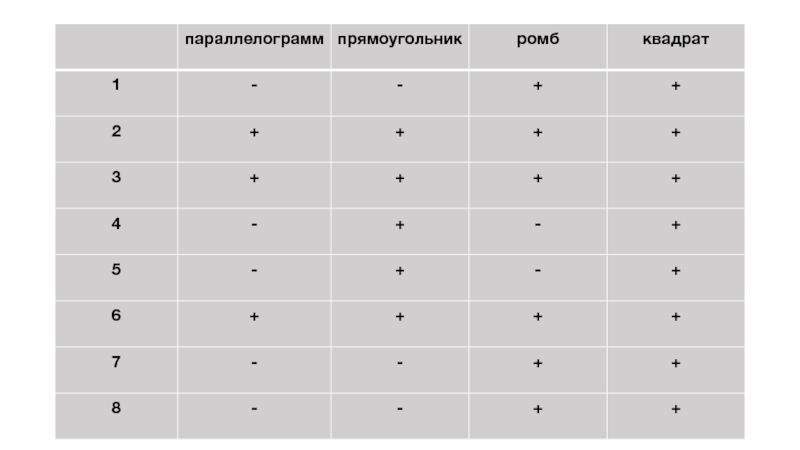
Слайд 18Сейчас вам предстоит заполнить таблицу, отметив знаками + (да) и –
(нет).
Вопросы:
Все стороны равны.
Противоположные стороны параллельны и равны.
Противолежащие углы равны, сумма соседних углов равна 180?.
Все углы прямые.
Диагонали равны.
Диагонали пересекаются и точкой пересечения делятся пополам.
Диагонали взаимно-перпендикулярны и являются биссектрисами его углов
Биссектриса угла отсекает от него равнобедренный треугольник.
Вопросы:
Все стороны равны.
Противоположные стороны параллельны и равны.
Противолежащие углы равны, сумма соседних углов равна 180?.
Все углы прямые.
Диагонали равны.
Диагонали пересекаются и точкой пересечения делятся пополам.
Диагонали взаимно-перпендикулярны и являются биссектрисами его углов
Биссектриса угла отсекает от него равнобедренный треугольник.
Слайд 20Паркетчик вырезал квадраты из дерева и проверял свою работу, сравнивая длины
их сторон. Если все четыре стороны были равны, то он считал квадрат вырезанным правильно. Надежна ли такая проверка?
Другой паркетчик проверял свою работу иначе. Он мерил не стороны квадрата, а их диагонали. Если обе диагонали оказывались равными, паркетчик считал квадрат, вырезанным правильно.
Вы тоже думаете. Что такая проверка правильно?
Другой паркетчик проверял свою работу иначе. Он мерил не стороны квадрата, а их диагонали. Если обе диагонали оказывались равными, паркетчик считал квадрат, вырезанным правильно.
Вы тоже думаете. Что такая проверка правильно?
Слайд 21Решение задач
Задача 1.
Меньшая сторона прямоугольника равна 4 см и образует с
диагональю
угол в 60°.Найдите диагонали прямоугольника.
Задача 2.
Сумма трёх углов параллелограмма равна 252°. Найдите углы
параллелограмма.
Задача 3.
Углы, образуемые стороной ромба с его диагоналями, относятся как
4:5. Вычислите углы ромба.
угол в 60°.Найдите диагонали прямоугольника.
Задача 2.
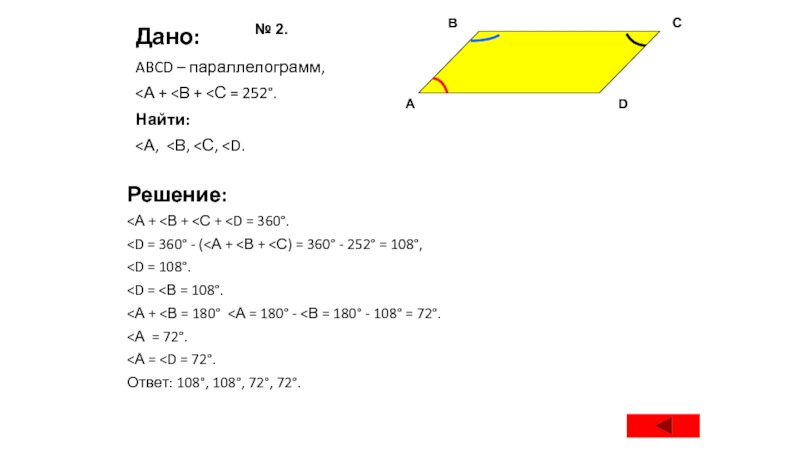
Сумма трёх углов параллелограмма равна 252°. Найдите углы
параллелограмма.
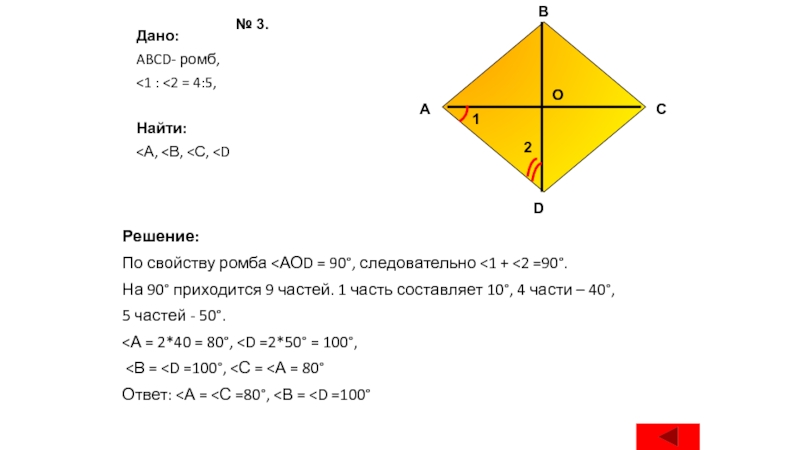
Задача 3.
Углы, образуемые стороной ромба с его диагоналями, относятся как
4:5. Вычислите углы ромба.
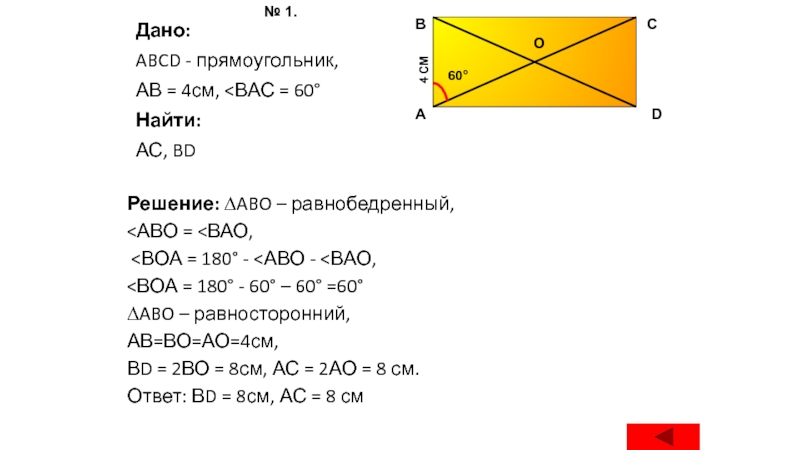
Слайд 22Дано:
ABCD - прямоугольник,
АВ = 4см,
∆ABO – равнобедренный,
<АВО = <ВАО,
<ВОА = 180° - <АВО - <ВАО,
<ВОА = 180° - 60° – 60° =60°
∆ABO – равносторонний,
АВ=ВО=АО=4см,
ВD = 2ВО = 8см, АС = 2АО = 8 см.
Ответ: ВD = 8см, АС = 8 см
<АВО = <ВАО,
<ВОА = 180° - <АВО - <ВАО,
<ВОА = 180° - 60° – 60° =60°
∆ABO – равносторонний,
АВ=ВО=АО=4см,
ВD = 2ВО = 8см, АС = 2АО = 8 см.
Ответ: ВD = 8см, АС = 8 см
А
D
С
В
4 СМ
60°
О
№ 1.
Слайд 23Дано:
ABCD – параллелограмм,
Решение: А D С В № 2.
<А + <В + <С +
<А = 72°.
<А =
Слайд 24Дано:
ABCD- ромб,
<АОD = 90°, следовательно <1 + <2 =90°.
На 90° приходится 9 частей. 1 часть составляет 10°, 4 части – 40°,
5 частей - 50°.
<А = 2*40 = 80°, <В = Ответ: <А = <С =80°, <В =
На 90° приходится 9 частей. 1 часть составляет 10°, 4 части – 40°,
5 частей - 50°.
<А = 2*40 = 80°,
А
D
С
В
1
2
О
№ 3.
Слайд 25№ 407 (геометрия 7-9 кл. Атанасян и др.)
Острый угол
ромба равен 30°. Найти высоту ромба, если
его периметр равен 16 см.
Длины оснований прямоугольной трапеции равны
10 и 6 см. Больший угол равен 120°. Найти большую
боковую сторону трапеции.
его периметр равен 16 см.
Длины оснований прямоугольной трапеции равны
10 и 6 см. Больший угол равен 120°. Найти большую
боковую сторону трапеции.
Домашнее задание
