- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии: Прямоугольный треугольник (7 класс)
Содержание
- 1. ПРезентация по геометрии: Прямоугольный треугольник (7 класс)
- 2. ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК-ЭТО ТРЕУГОЛЬНИК, В КОТОРОМ ОДИН ИЗ УГЛОВ ПРЯМОЙ (90°)
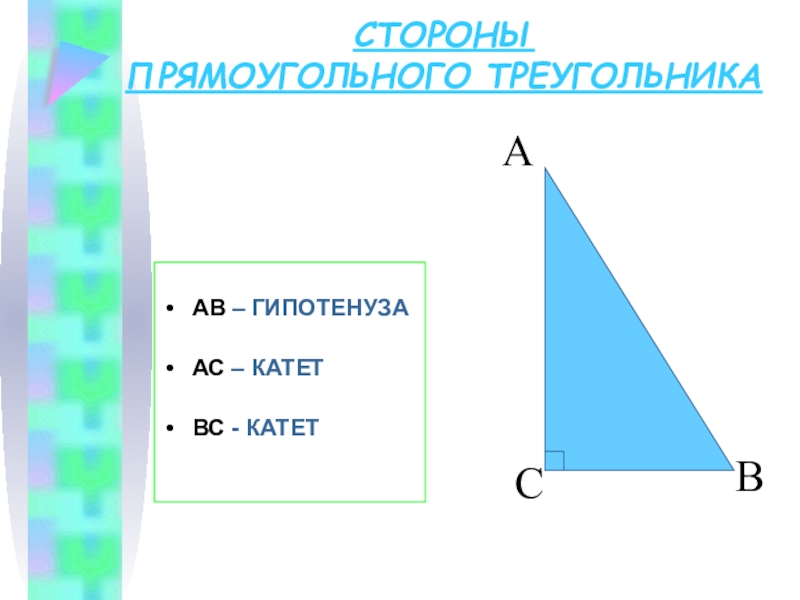
- 3. СТОРОНЫ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКААВ – ГИПОТЕНУЗААС – КАТЕТВС - КАТЕТ АВС
- 4. ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
- 5. 1. Если катеты одного прямоугольного треугольника соответственно
- 6. 2. Если катет и прилежащий к нему
- 7. 3. Если гипотенуза и острый угол одного
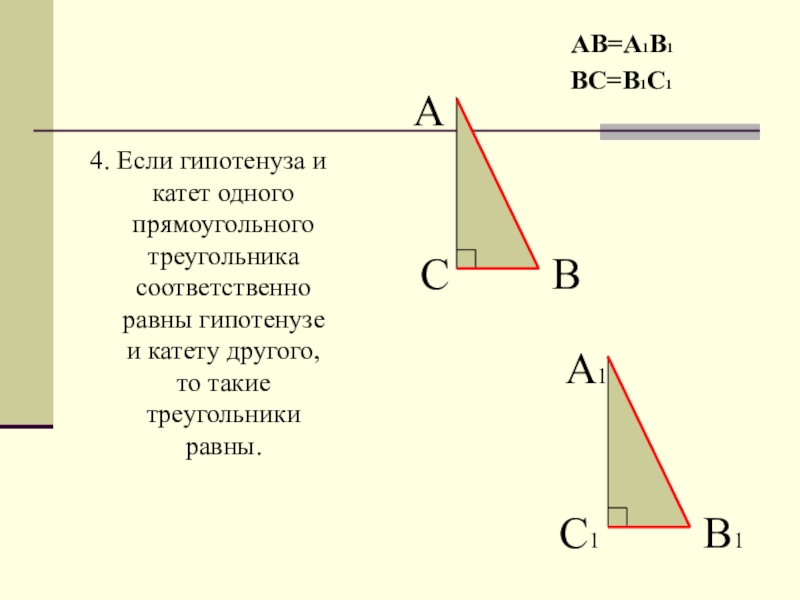
- 8. 4. Если гипотенуза и катет одного прямоугольного
- 9. НЕКОТОРЫЕ СВОЙСТВА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
- 10. ТЕОРЕМА ПИФАГОРА В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.ВСА
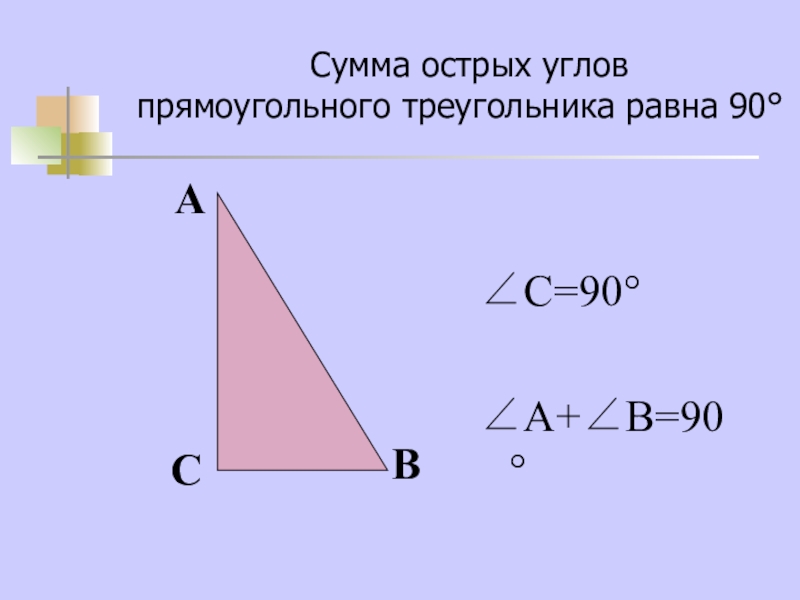
- 11. Сумма острых углов прямоугольного треугольника равна 90°∠С=90°∠А+∠В=90°САВ
- 12. В прямоугольном равнобедренном треугольнике острые углы равны 45°.∠С = 90°АС=ВС ∠А=45° ∠В=45°АВС
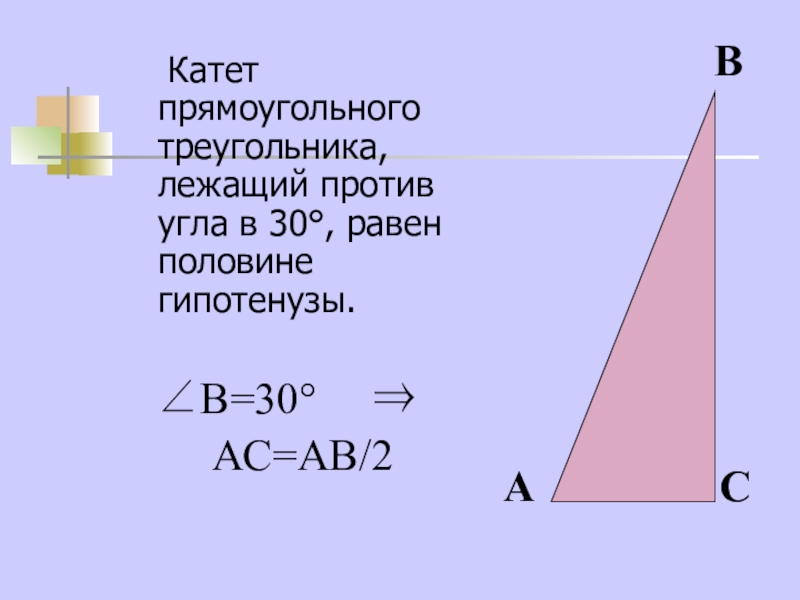
- 13. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.∠В=30° ⇒ АС=АВ/2АВС
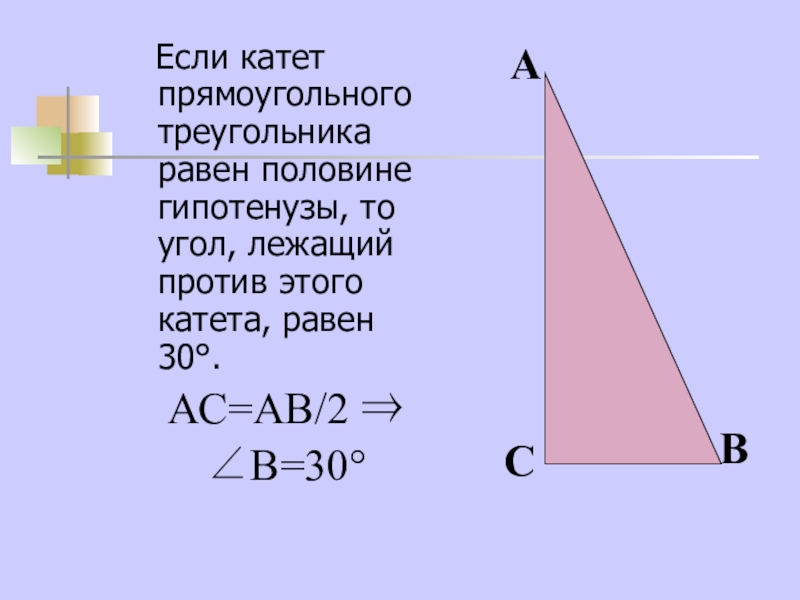
- 14. Если катет прямоугольного треугольника равен
- 15. Высота прямоугольного треугольника, проведённая из
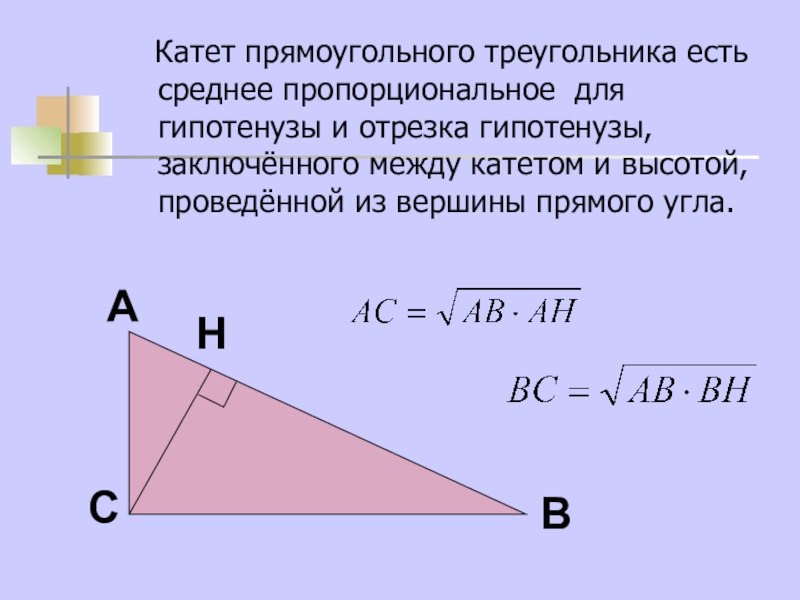
- 16. Катет прямоугольного треугольника есть среднее
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК-ЭТО ТРЕУГОЛЬНИК, В КОТОРОМ ОДИН ИЗ УГЛОВ ПРЯМОЙ (90°)
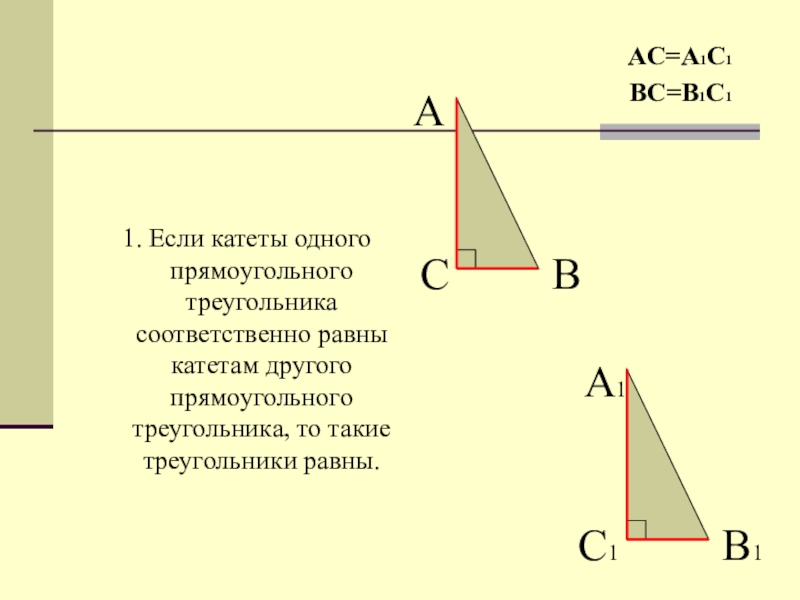
Слайд 51. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного
треугольника, то такие треугольники равны.
АС=А1С1
ВС=В1С1
А
В
С
А1
В1
С1
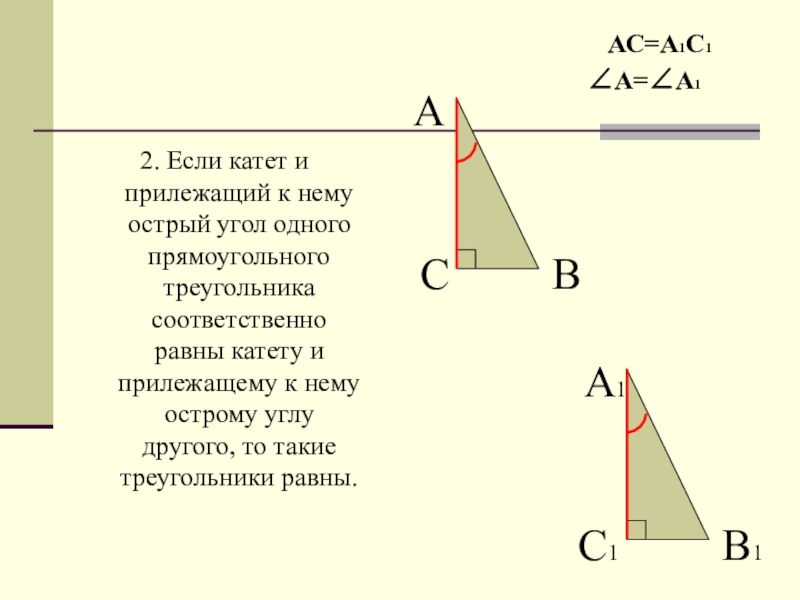
Слайд 62. Если катет и прилежащий к нему острый угол одного прямоугольного
треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
АС=А1С1
∠А=∠А1
А
В
С
А1
В1
С1
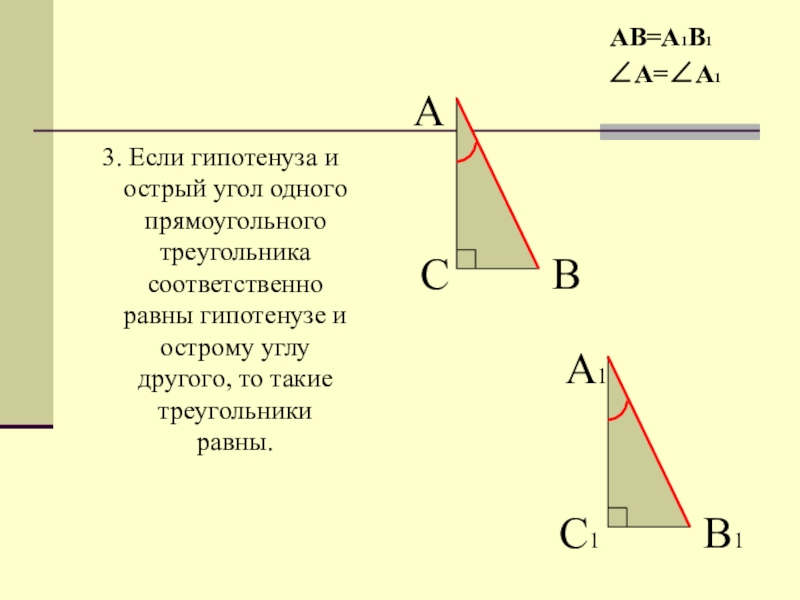
Слайд 73. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны
гипотенузе и острому углу другого, то такие треугольники равны.
АВ=А1В1
∠А=∠А1
А
В
С
А1
В1
С1
Слайд 84. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе
и катету другого, то такие треугольники равны.
АВ=А1В1
ВС=В1С1
А
В
С
А1
В1
С1
Слайд 10ТЕОРЕМА ПИФАГОРА
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов.
В
С
А
Слайд 12В прямоугольном равнобедренном треугольнике острые углы равны 45°.
∠С = 90°
АС=ВС
∠А=45°
∠В=45°
А
В
С
Слайд 13 Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
∠В=30°
⇒
АС=АВ/2
АС=АВ/2
А
В
С
Слайд 14 Если катет прямоугольного треугольника равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.
АС=АВ/2 ⇒
∠В=30°
АС=АВ/2 ⇒
∠В=30°
А
В
С
Слайд 15
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть
среднее пропорциональное для отрезков, на которые делится гипотенуза высотой.
С
А
Н
В
Слайд 16 Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и
отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.
С
А
Н
В
