- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Правило параллелепипеда (10 класс)
Содержание
Правило параллелепипедаРассмотрим некомпланарные векторы , и .От произвольной точки О пространства отложим векторы , и , равные векторам
Слайд 2Правило параллелепипеда
Рассмотрим некомпланарные векторы , и
.
От произвольной точки О пространства отложим векторы , и
, равные векторам , и
На полученных векторах можно построить параллелепипед так, чтобы они являлись его рёбрами.
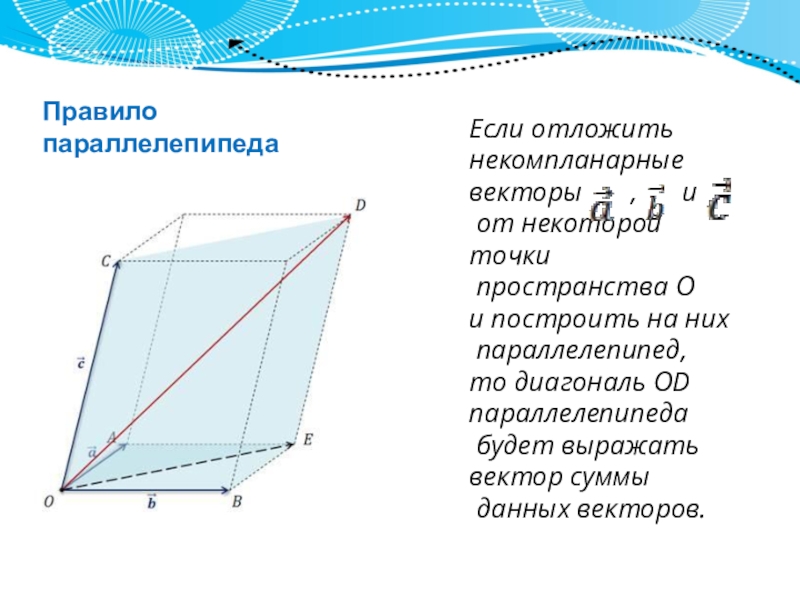
Слайд 3Если отложить
некомпланарные
векторы , и
от
некоторой точки
пространства О
и построить на них
параллелепипед,
то диагональ OD
параллелепипеда
будет выражать
вектор суммы
данных векторов.
пространства О
и построить на них
параллелепипед,
то диагональ OD
параллелепипеда
будет выражать
вектор суммы
данных векторов.
Правило параллелепипеда
Слайд 4Рассмотрим
параллелепипед. Найти
Так как эти векторы отложены от одной точки и являются рёбрами данного параллелепипеда, то вектор их суммы будет задавать диагональ параллелепипеда,
одним из концов которой будет точка начала данных векторов А. Так мы получим вектор .
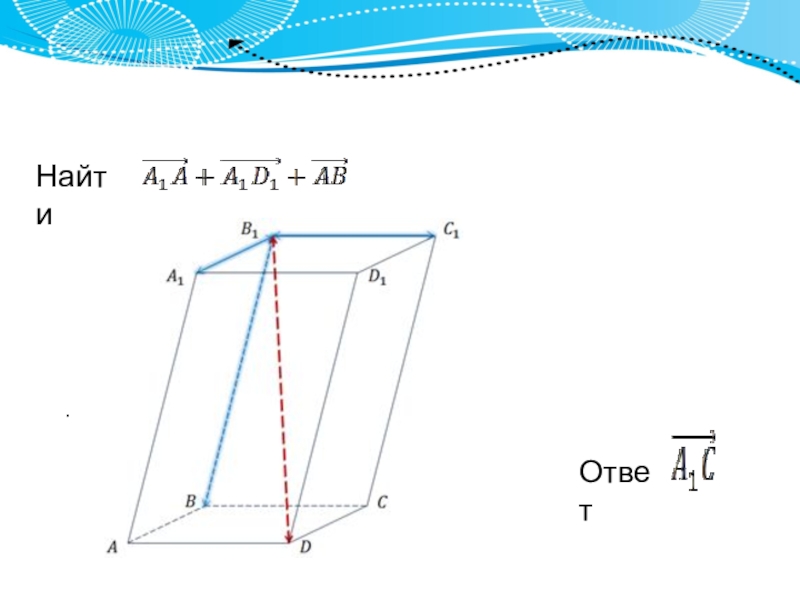
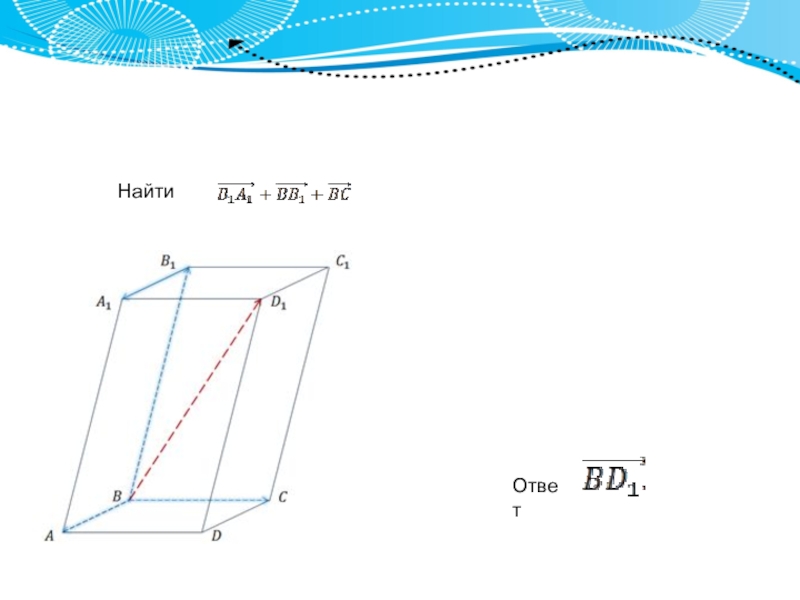
Слайд 5 Найти
.
В данном случае векторы не имеют общего начала, а
имеют общий конец.
Выразим каждый из данных векторов через противоположный.
Выразим каждый из данных векторов через противоположный.
