Судиславль
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Правильные многоугольники
Содержание
- 1. Презентация по геометрии Правильные многоугольники
- 2. ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИКПравильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
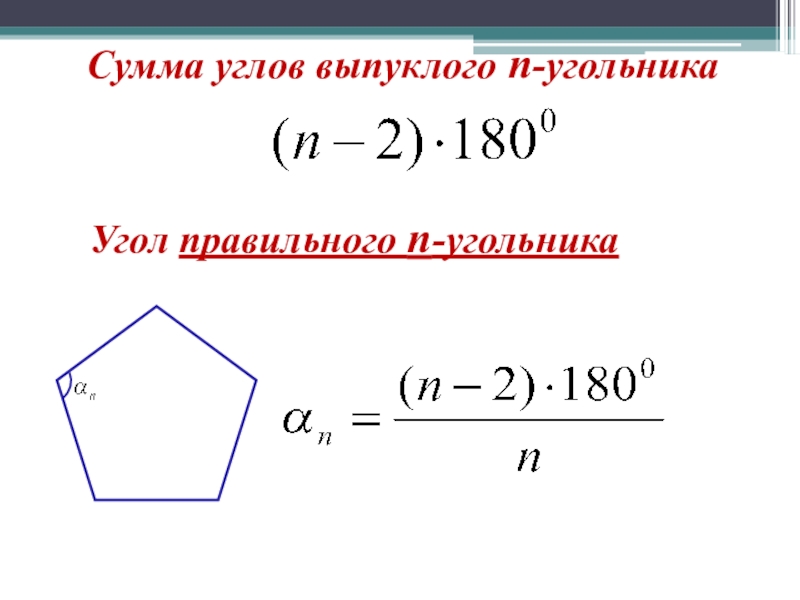
- 3. Сумма углов выпуклого n-угольникаУгол правильного n-угольника
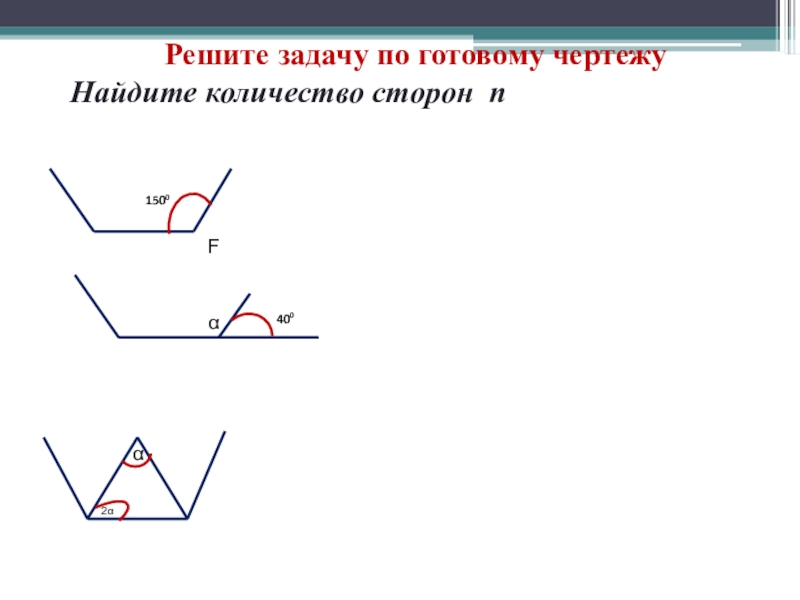
- 4. Решите задачу по готовому чертежуНайдите количество сторон nF1500400α2αα
- 5. Вписанный и описанный многоугольникмногоугольник называется вписанным в
- 6. Вписанная и описанная окружности правильного многоугольника имеют
- 7. Центральный угол многоугольникаУгол, под которым видна сторона
- 8. Задача.Вычислите центральный угол правильногоА) четырехугольника Б) десятиугольникаВ) двенадцатиугольника
- 9. Задача. Найдите количество сторон правильного многоугольника,
- 10. 1. Любой правильный
- 11. В таблице заполните пустые клетки (αn-угол
- 12. Решение задач.1) Дано: αn = 108°
- 13. Решение задач. Решение:
- 14. Решение задач.2) Дано: n = 20
- 15. Решение задач.1. Sn = 180°(n -2)
- 16. Решение задач.3) Дано: Sn = 1260°
- 17. Решение задач.Решение: 1. 1260°= 180°(n
ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИКПравильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Слайд 1ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Автор:
Мохова Александра Вячеславовна,
учитель математики
Муниципальное общеобразовательное учреждение
Судиславская средняя общеобразовательная школа
п.
Слайд 2ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК
Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны
и все стороны равны.
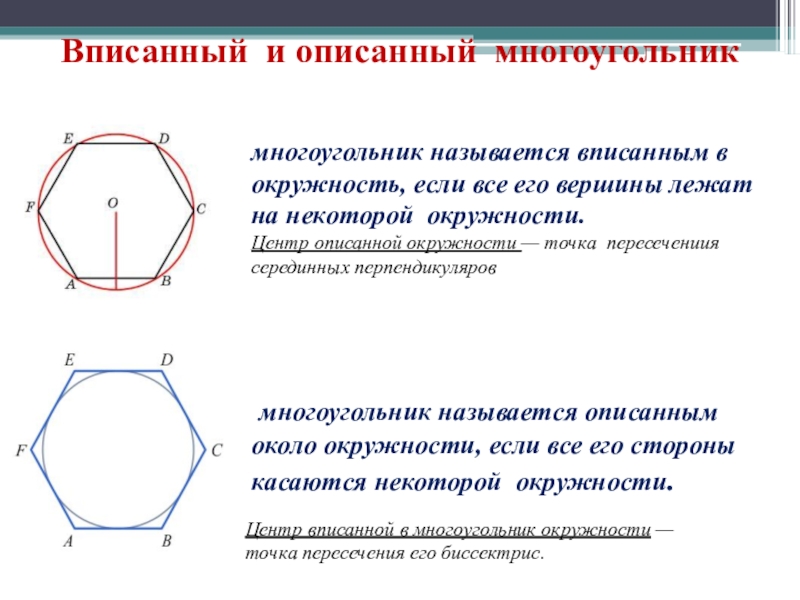
Слайд 5Вписанный и описанный многоугольник
многоугольник называется вписанным в окружность, если все его
вершины лежат на некоторой окружности.
Центр описанной окружности — точка пересечениия серединных перпендикуляров
многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
Центр описанной окружности — точка пересечениия серединных перпендикуляров
многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
Центр вписанной в многоугольник окружности — точка пересечения его биссектрис.
Слайд 6Вписанная и описанная окружности правильного многоугольника имеют один и тот же
центр.
Его называют центром многоугольника
R – радиус описанной окружности
r – вписанной окружности
Его называют центром многоугольника
R – радиус описанной окружности
r – вписанной окружности
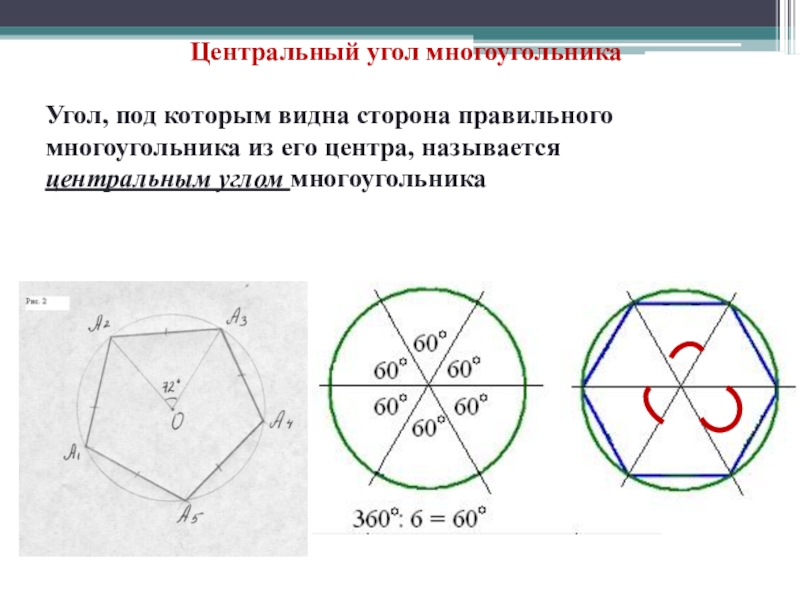
Слайд 7Центральный угол многоугольника
Угол, под которым видна сторона правильного многоугольника из
его центра, называется
центральным углом многоугольника
центральным углом многоугольника
Слайд 8
Задача.
Вычислите центральный угол правильного
А) четырехугольника
Б) десятиугольника
В) двенадцатиугольника
Слайд 9Задача. Найдите количество сторон правильного многоугольника, центральный угол которого равен: 1)120°
2)60°
3)72°
Слайд 10
1. Любой правильный многоугольник является выпуклым.
2.
Любой выпуклый многоугольник является правильным.
3. Многоугольник является правильным,
если он выпуклый и все его стороны равны.
4. Многоугольник является правильным,
если он выпуклый и все его углы равны.
5. Любой четырехугольник с равными сторонами является правильным.
6. Любой четырехугольник с равными углами является правильным.
7. Любой правильный четырехугольник
является квадратом
3. Многоугольник является правильным,
если он выпуклый и все его стороны равны.
4. Многоугольник является правильным,
если он выпуклый и все его углы равны.
5. Любой четырехугольник с равными сторонами является правильным.
6. Любой четырехугольник с равными углами является правильным.
7. Любой правильный четырехугольник
является квадратом
Слайд 11 В таблице заполните пустые клетки (αn-угол правильного n-угольника, n-сторон, S n-
сумма углов правильного n-угольника).
Решение задач записать в тетрадь.
Слайд 13Решение задач.
Решение:
1. n · αn = 180°(n -2) 2. Sn = n · αn
108° n = 180°(n -2) Sn = 108° · 5 = 540°
3. 72° n = 360°
n = 5
Ответ: n = 5 и S5= 540°
Слайд 15Решение задач.
1. Sn = 180°(n -2)
2. αn = Sn : n
Sn = 180°(20 - 2) α20 = 3240° : 20 = 162°
Sn = 3240°
Sn = 180°(20 - 2) α20 = 3240° : 20 = 162°
Sn = 3240°
Ответ: α20 = 162° и S20= 3240°
Слайд 17Решение задач.
Решение:
1. 1260°= 180°(n - 2)
2.αn = 1260° : 9 = 140°
1260°= 180°n - 360°
180°n =360°+ 1260°
n = 9
1260°= 180°n - 360°
180°n =360°+ 1260°
n = 9
Ответ: α9 = 140° и n = 9.
