- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии подобие пространственных фигур
Содержание
- 1. Презентация по геометрии подобие пространственных фигур
- 2. Преобразование подобия Если при преобразовании фигуры F
- 3. Свойства преобразования подобияПреобразование подобия переводит прямые в
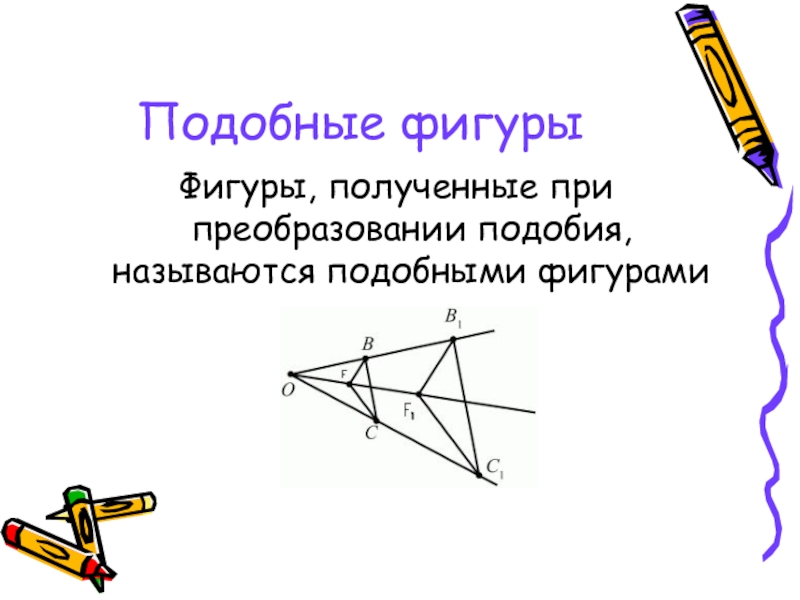
- 4. Подобные фигурыФигуры, полученные при преобразовании подобия, называются
- 5. Свойства подобных фигурЕсли фигура F1 подобна фигуре
- 6. Гомотетия - один из видов преобразования подобия
- 7. Гомотетия с центром O и коэффициентом k — это преобразование, в котором каждая точка P отображается такой точкой P1,что OP1=k⋅OP,гдеk≠0
- 8. Чтобы гомотетия была определена, должен быть задан
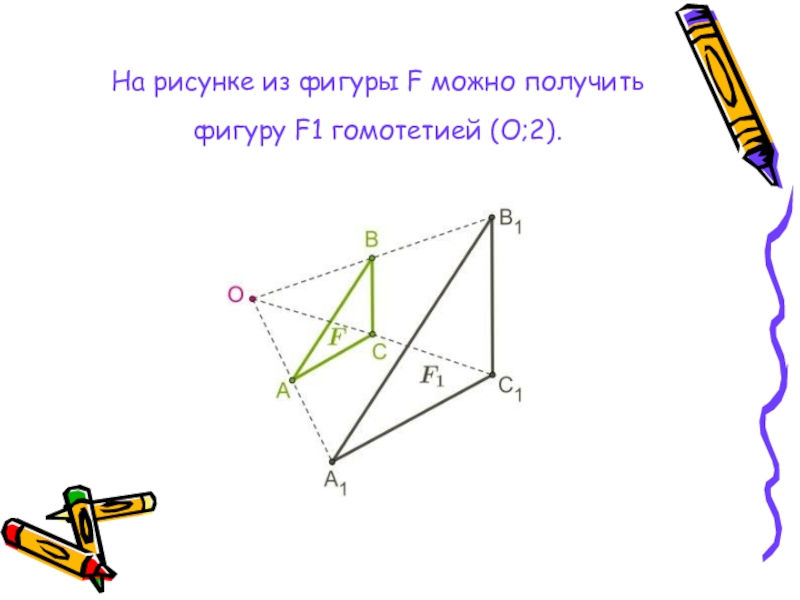
- 9. На рисунке из фигуры F можно получить фигуру F1 гомотетией (O;2).
- 10. Если фигуры находятся на противоположных направлениях от
- 11. Центр гомотетии может находиться и внутри фигуры. Серый треугольник из зелёного треугольника ABC получен гомотетией (O; 1/2).
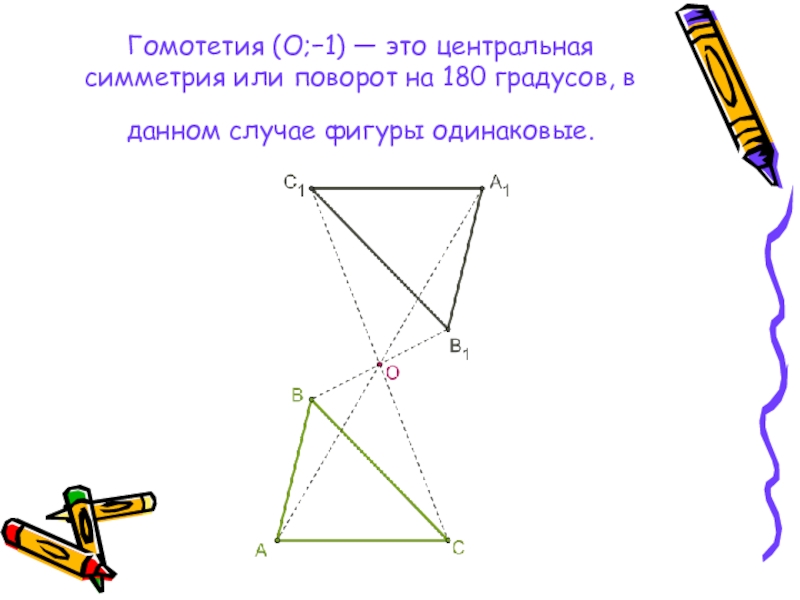
- 12. Гомотетия (O;−1) — это центральная симметрия или поворот на 180 градусов, в данном случае фигуры одинаковые.
- 13. Формулы гомотетии с центром в начале координат и коэффициентом kХ’=kxY’=kyZ’=kz
- 14. Cвойства гомотетии1)При гомотетии величина плоского и двухгранного
- 15. 6) Преобразование гомотетии в пространстве переводит любую
- 16. Подобие в жизни
- 17. Слайд 17
- 18. Слайд 18
- 19. Проверь себя:1. Подобные фигуры это фигуры, полученные
- 20. Ответы+----
Преобразование подобия Если при преобразовании фигуры F в фигуру F` расстояние между точками изменяется в одно и тоже число раз, то такое преобразование называется преобразованием подобия. Т.е. произвольные точки AB фигуры F переходят в точки A`B`
Слайд 2Преобразование подобия
Если при преобразовании фигуры F в фигуру F` расстояние между
точками изменяется в одно и тоже число раз, то такое преобразование называется преобразованием подобия. Т.е. произвольные точки AB фигуры F переходят в точки A`B` фигуры F`, так что A`B` =k*AB. Число k – это коэффициент подобия.
Слайд 3Свойства преобразования подобия
Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые,
отрезки в отрезки.
Преобразование подобия сохраняет углы между полупрямыми.
Точки, лежащие на прямой при преобразовании подобия переходят в точки, лежащие на прямой, а также сохраняется порядок их взаиморасположения.
Преобразование подобия сохраняет углы между полупрямыми.
Точки, лежащие на прямой при преобразовании подобия переходят в точки, лежащие на прямой, а также сохраняется порядок их взаиморасположения.
Слайд 5Свойства подобных фигур
Если фигура F1 подобна фигуре F2, а фигура F2
подобна фигуре F3, то фигура F1 подобна фигуре F3.
У подобных фигур соответствующие углы равны.
Соответствующие отрезки у подобных фигур пропорциональны, т.е. изменены в одно и то число раз.
У подобных фигур соответствующие углы равны.
Соответствующие отрезки у подобных фигур пропорциональны, т.е. изменены в одно и то число раз.
Слайд 7
Гомотетия с центром O и коэффициентом k — это преобразование, в котором каждая точка P отображается такой точкой P1,что
OP1=k⋅OP,гдеk≠0
Слайд 8
Чтобы гомотетия была определена, должен быть задан центр гомотетии и коэффициент.
Это можно записать так: гомотетия (O;k).
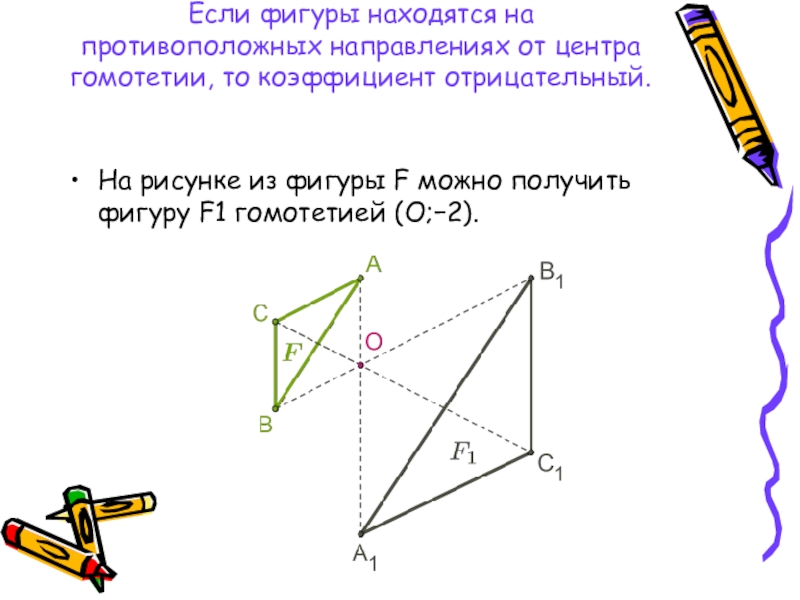
Слайд 10Если фигуры находятся на противоположных направлениях от центра гомотетии, то коэффициент
отрицательный.
На рисунке из фигуры F можно получить фигуру F1 гомотетией (O;−2).
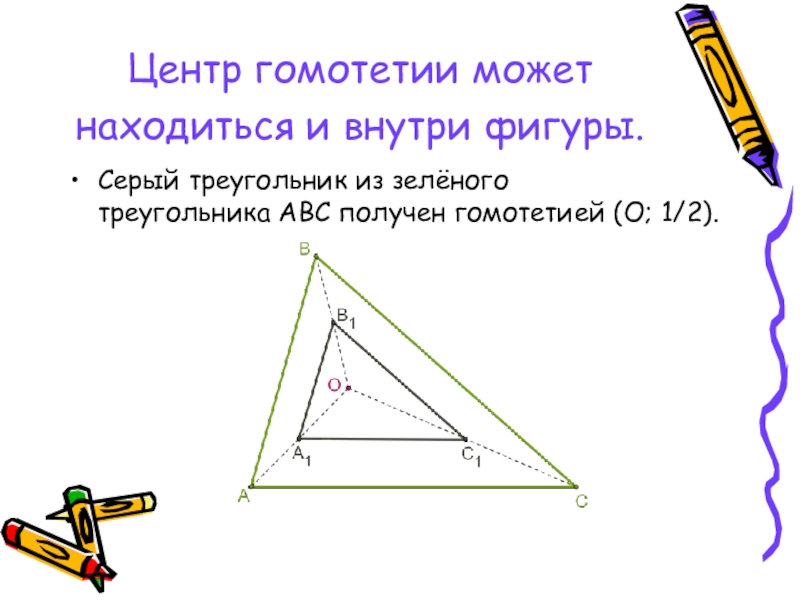
Слайд 11Центр гомотетии может находиться и внутри фигуры.
Серый треугольник из зелёного
треугольника ABC получен гомотетией (O; 1/2).
Слайд 12Гомотетия (O;−1) — это центральная симметрия или поворот на 180 градусов, в данном случае фигуры одинаковые.
Слайд 14Cвойства гомотетии
1)При гомотетии величина плоского и двухгранного угла сохраняется.
2)При гомотетии с
коэффициентом k расстояние между точками изменяется в lkl раз
3)Отношение площадей гомотетических фигур равно квадрату коэффициента гомотетии.
4)Отношение объемов гомотетических фигур равно модулю куба коэффициента гомотетии.
5)Гомотетия с положительным коэффициентом не меняет ориентации пространства, а с отрицательным меняет.
3)Отношение площадей гомотетических фигур равно квадрату коэффициента гомотетии.
4)Отношение объемов гомотетических фигур равно модулю куба коэффициента гомотетии.
5)Гомотетия с положительным коэффициентом не меняет ориентации пространства, а с отрицательным меняет.
Слайд 156) Преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через
центр гомотетии, в параллельную плоскость (или в себя, при k=1)
Слайд 19Проверь себя:
1. Подобные фигуры это фигуры, полученные при преобразовании подобия.
2. Если
фигура F1 подобна фигуре F2, а фигура F2 подобна фигуре F3, то фигура F1 не подобна фигуре F3.
Преобразование подобия переводит прямые в полупрямые, а отрезки в отрезки.
При гомотетии величина плоского угла остается та же, а величина двухгранного угла меняется.
Отношение объемов гомотетических фигур равно модулю квадрата коэффициента гомотетии
Преобразование подобия переводит прямые в полупрямые, а отрезки в отрезки.
При гомотетии величина плоского угла остается та же, а величина двухгранного угла меняется.
Отношение объемов гомотетических фигур равно модулю квадрата коэффициента гомотетии