- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Задачи на построения
Содержание
- 1. Презентация по геометрии по теме Задачи на построения
- 2. ЗадачаРазделить отрезок длиной 5 см на четыре
- 3. Слайд 3
- 4. Задачи на построение Тема урока:Учебная задача урока:
- 5. В геометрии выделяют задачи
- 6. O
- 7. Дано: отрезок АВ, луч ОС. Построили: OD=
- 8. Схема решения задач на построение:Анализ (рисунок искомой
- 9. Задача2.Построить треугольник, стороны которого равны заданным отрезкам.Дано:
- 10. Доказательство:В ΔАВС АВ=а=3см по построению как радиус
- 11. Учебник, задача №148 На прямой даны две
- 12. Учебник, задача №149 Даны прямая а
- 13. Дано: А
- 14. Доказательство:У них АМ=АК=ВМ=ВК как радиусы однойокружности,Значит, ΔАМК
- 15. Задача 4. Разделить отрезок длиной 5 см
- 16. Построение: 1) Луч АМАМ2) окр.1(А, r=АВ) 3)
- 17. Доказательство: А
- 18. АВСДано:Построить: Построение:окр.1 (А ,r)окр.1 (А, r) Ո
- 19. Дано: угол А.АПостроили: угол О.ВСОDEДоказательство: рассмотрим ΔАВС
- 20. Задача 6.Построить треугольник по двум сторонам и углу между нимиДано:а=3смb=4смОПостроить:ΔАВС, АВ=а=3см, АС=b=4см,Анализ:b=4сма=3смАВС
- 21. Построение:1) Луч АМАМО2) окр.1 (О, r)3) окр.1
- 22. Доказательство:В ΔАВС :АВ=а=3см как радиусы одной окружностиАС=b=4см
- 23. САМОСТОЯТЕЛЬНОЗадача 7:Построить треугольник по стороне и двум прилежащим углам Дано:а=5смОЕ
- 24. Дано: угол АПостроить: биссектрису АВПостроение:1) окр.1 (A,
- 25. Докажем, что луч АВ – биссектриса
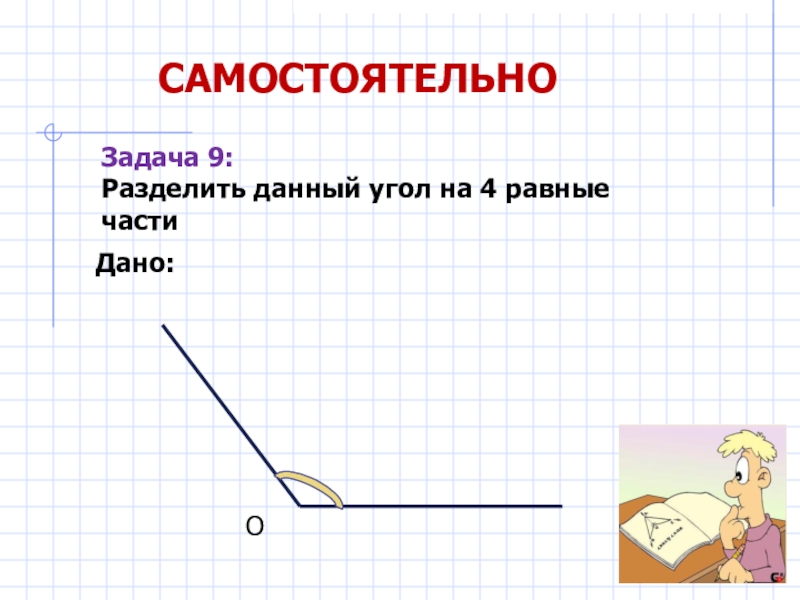
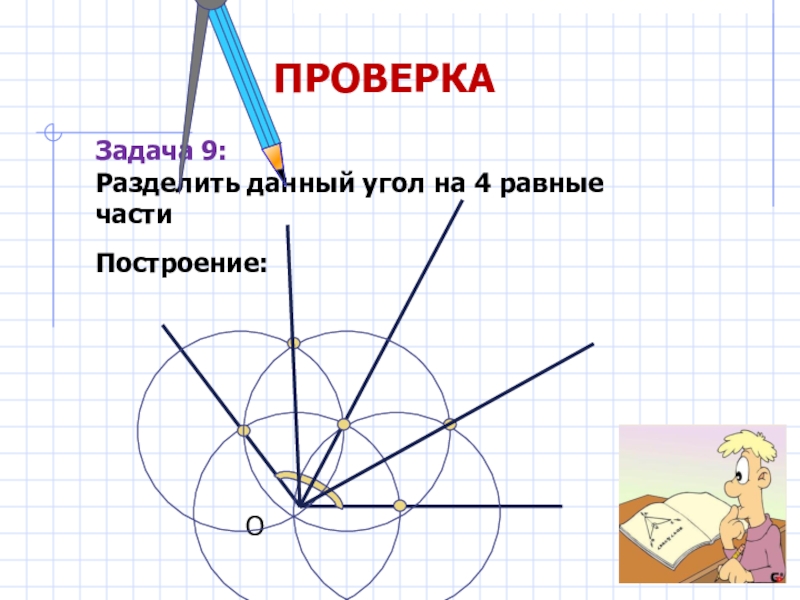
- 26. САМОСТОЯТЕЛЬНОЗадача 9:Разделить данный угол на 4 равные частиДано:О
- 27. ПРОВЕРКАЗадача 9:Разделить данный угол на 4 равные частиПостроение:О
- 28. Задача 10.Построить точку пересечения биссектрис треугольникаДано:А1В1С1Построить: ΔАВС
- 29. Дано:А1В1С1Построение:1) Луч АМАМ2) окр.1(А, r=А1С1) С3) окр.1
- 30. Задача 11.Дана прямая m и точка A,
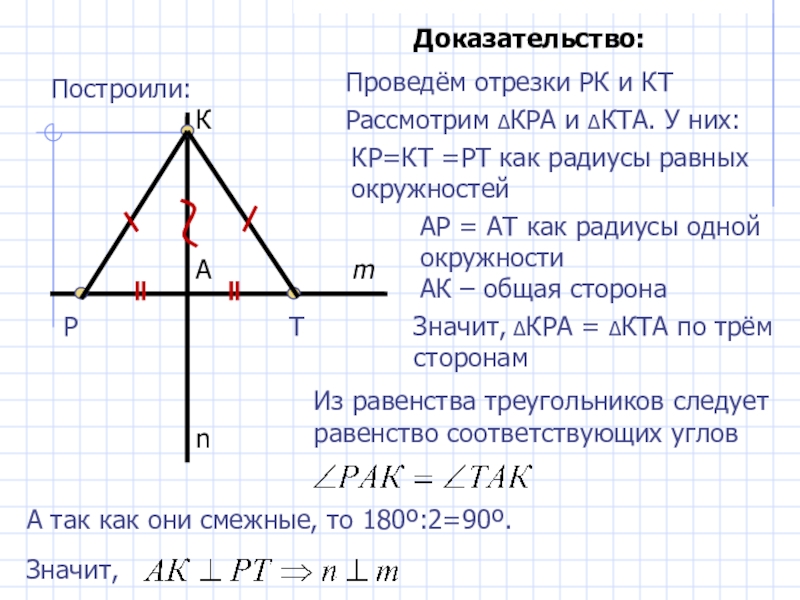
- 31. Построили:mnАPТКДоказательство:Проведём отрезки РК и КТРассмотрим ΔКРА и
- 32. Работа в пареУчебник, задача №153 Даны прямая
- 33. Дано:b=3сма=5 смПостроить: Построение:mА1) окр.1(А, r)2) окр.1
- 34. Самостоятельная работаПервый вариантПостроить прямоугольный треугольник по катету
- 35. 1. Укажите, какое из указанных дальше построений
- 36. 2. Укажите, какое из приведенных дальше построений
- 37. ТЕСТ3. Треугольник можно построить из трех отрезков,
- 38. 4. Треугольник АВС можно построить, если:А)Б) АВ
- 39. ТЕСТ5. Геометрическим местом точек плоскости, равноудаленных от
- 40. 6. Какую фигуру образуют все точки плоскости,
- 41. ТЕСТ7. Геометрическим местом точек угла, равноудаленных от
- 42. ТЕСТ8. Какое из утверждений неправильное: А) С
- 43. ТЕСТ9. Какую фигуру образуют все точки плоскости,
- 44. ТЕСТ10. Какая из задач не является основной
- 45. ПРОВЕРЬ СЕБЯ
- 46. Спасибо за внимание!
Слайд 1Задачи на построение
Урок геометрии в 7 классе
Презентацию подготовила
Рудник Ольга Анатольевна
учитель
МОУ «СШ№53 г. Макеевки»
Слайд 2Задача
Разделить отрезок длиной 5 см на четыре равные части
Разделить угол 55º
Расположить три точки на одинаковом расстоянии друг
от друга
Слайд 4Задачи на построение
Тема урока:
Учебная задача урока:
дать представление о задачах
Слайд 5 В геометрии выделяют задачи на построение, которые можно
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
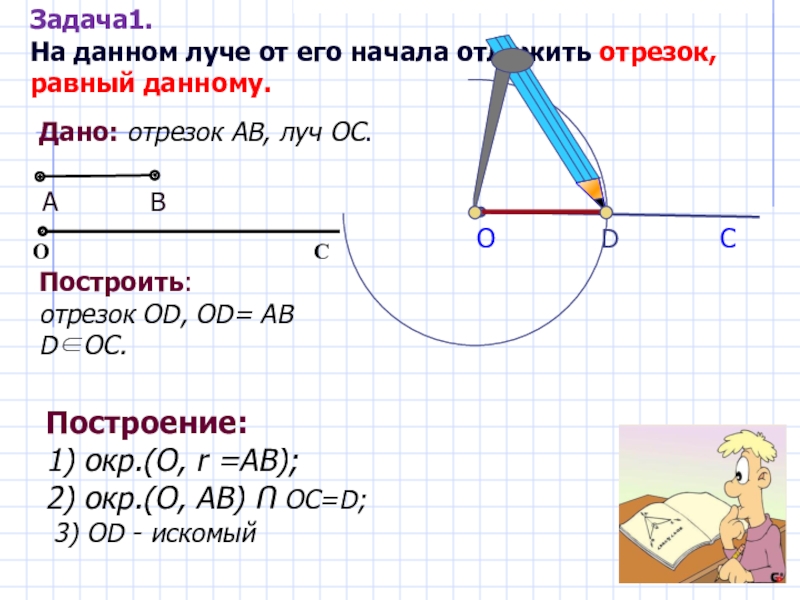
Слайд 6
O
Дано: отрезок АВ, луч ОС.
Построить:
отрезок OD, OD= АВ D∈ОС.
Построение:
1) окр.(O, r =АВ);
2) окр.(O, АВ) Ո OC=D;
3) OD - искомый
Задача1.
На данном луче от его начала отложить отрезок, равный данному.
D
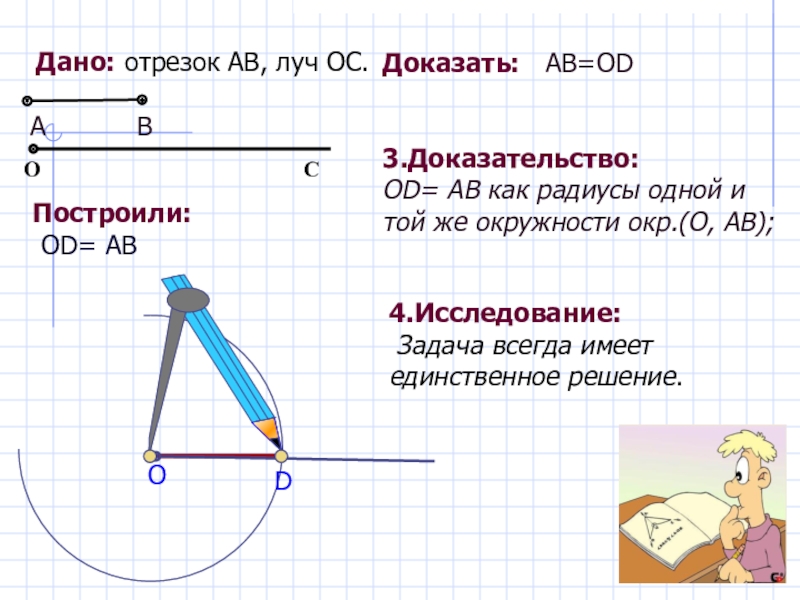
Слайд 7Дано: отрезок АВ, луч ОС.
Построили:
OD= АВ
Доказать:
3.Доказательство:
OD= АВ как радиусы одной и той же окружности окр.(O, АВ);
4.Исследование:
Задача всегда имеет единственное решение.
Слайд 8Схема решения задач на построение:
Анализ (рисунок искомой фигуры, установление связей между
Построение по намеченному плану.
Доказательство, что данная фигура удовлетворяет условиям задачи.
Исследование (когда и сколько задача имеет решений?).
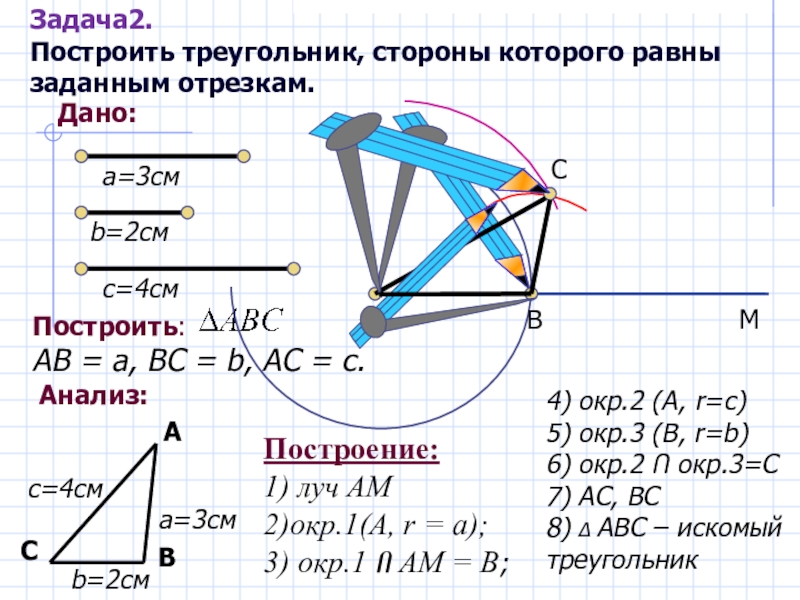
Слайд 9Задача2.
Построить треугольник, стороны которого равны заданным отрезкам.
Дано:
а=3см
b=2см
с=4см
Построить:
АВ = а, ВС = b, AC = c.
Построение:
1) луч АМ
2)окр.1(А, r = а);
3) окр.1 Ո АМ = В;
А
М
В
4) окр.2 (А, r=с)
5) окр.3 (В, r=b)
6) окр.2 Ո окр.3=С
7) AC, BC
8) Δ АВС – искомый треугольник
С
Анализ:
а=3см
b=2см
с=4см
С
В
А
Слайд 10Доказательство:
В ΔАВС АВ=а=3см по построению как радиус окр.(А,r=a), АС=с=4см по построению
Исследование: Задача всегда имеет единственное решение.
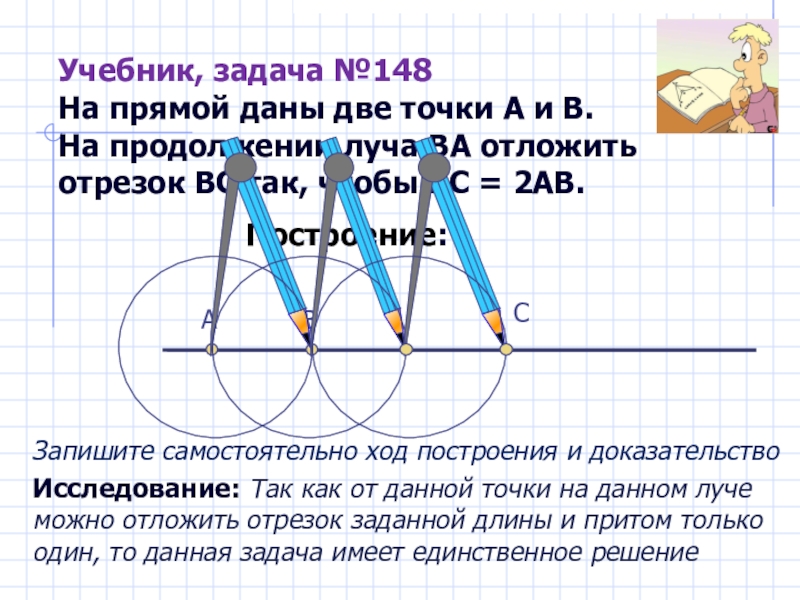
Слайд 11Учебник, задача №148 На прямой даны две точки А и В. На
Построение:
А
В
С
Запишите самостоятельно ход построения и доказательство
Исследование: Так как от данной точки на данном луче можно отложить отрезок заданной длины и притом только один, то данная задача имеет единственное решение
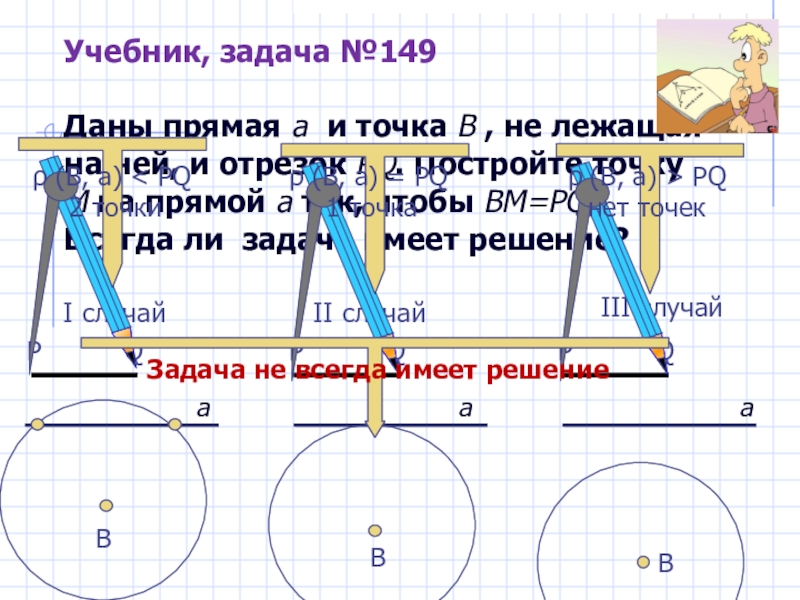
Слайд 12Учебник, задача №149 Даны прямая а и точка В , не лежащая
I случай
II случай
III случай
В
В
В
а
а
а
P Q
P Q
P Q
ρ (В, а) < PQ
2 точки
ρ (В, а) = PQ
1 точка
ρ (В, а) > PQ нет точек
Задача не всегда имеет решение
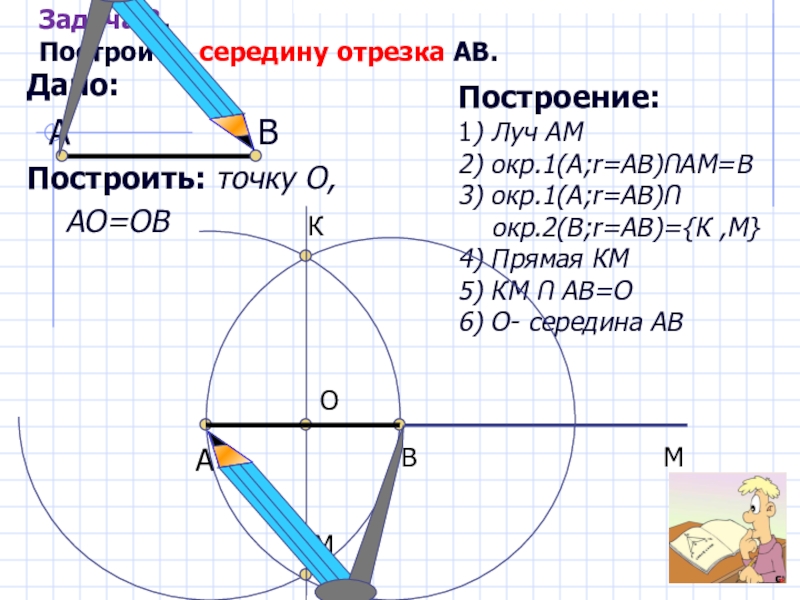
Слайд 13Дано:
А В
Построить:
АО=ОВ
Задача 3.
Построить середину отрезка АВ.
Построение:
1) Луч АМ
2) окр.1(А;r=AB)ՈАМ=В
3) окр.1(А;r=AB)Ո
окр.2(В;r=AB)={К ,М}
4) Прямая КМ
5) КМ Ո АВ=О
6) О- середина АВ
А
В
К
М
О
М
Слайд 14Доказательство:
У них АМ=АК=ВМ=ВК как радиусы одной
окружности,
Значит, ΔАМК = ΔВМК по трем
Рассмотрим ΔАМК и ΔВМК.
МК – общая сторона.
тогда соответствующие углы равны
В равнобедренном ΔАКВ (АК=КВ) КО является биссектрисой и медианой.
Значит, О – середина АВ, ч. и т. д.
Исследование: Задача всегда имеет единственное решение.
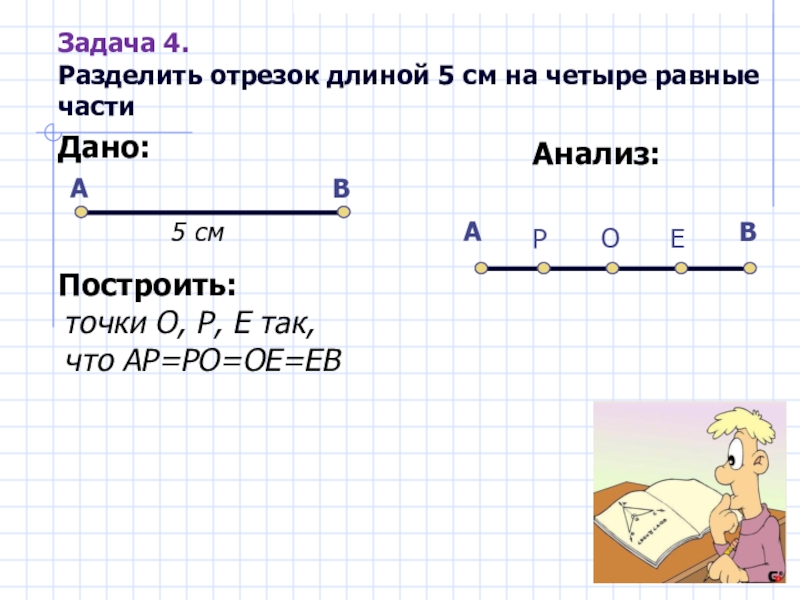
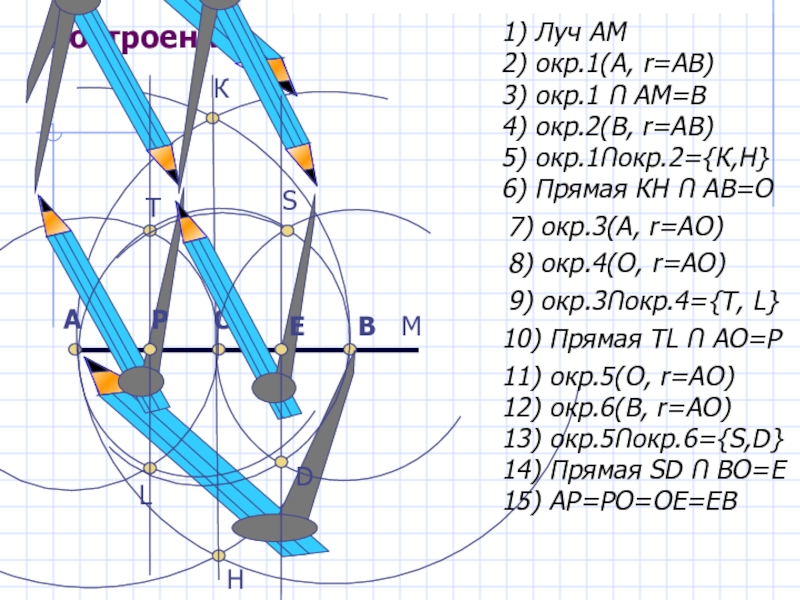
Слайд 15Задача 4.
Разделить отрезок длиной 5 см на четыре равные части
Дано:
А
В
5
Построить:
точки О, Р, Е так, что АР=РО=ОЕ=ЕВ
Анализ:
А
В
О
Р
Е
Слайд 16Построение:
1) Луч АМ
А
М
2) окр.1(А, r=АВ)
3) окр.1 Ո АМ=В
В
4) окр.2(В,
5) окр.1Ոокр.2={К,Н}
К
Н
6) Прямая КН Ո АВ=О
О
7) окр.3(А, r=АО)
8) окр.4(О, r=АО)
9) окр.3Ոокр.4={T, L}
L
T
10) Прямая TL Ո AO=P
P
11) окр.5(O, r=АО)
12) окр.6(В, r=АО)
13) окр.5Ոокр.6={S,D}
S
D
14) Прямая SD Ո BO=E
E
15) AP=PO=OE=EB
Слайд 17Доказательство: А Р
О – середина АВ по построению, тогда АО=ОВ=0,5 АВ
Р – середина АО и Е – середина ВО по построению, тогда АР=РО=ОЕ=ЕВ=0,25 АВ
Значит, отрезок АВ разделили на четыре равные части
Исследование:
Задача всегда имеет единственное решение.
Слайд 18
А
В
С
Дано:
Построить:
Построение:
окр.1 (А ,r)
окр.1 (А, r) Ո
окр.2 (O, AC)
окр.2 Ո ОМ = D
окр.3 (B, BC)
окр.4 (D, BC)
окр.2 Ո окр.4 = E
8) луч ОЕ
9) искомый.
О
D
E
Задача 5.
Отложить от данного луча угол, равный данному
М
Слайд 19
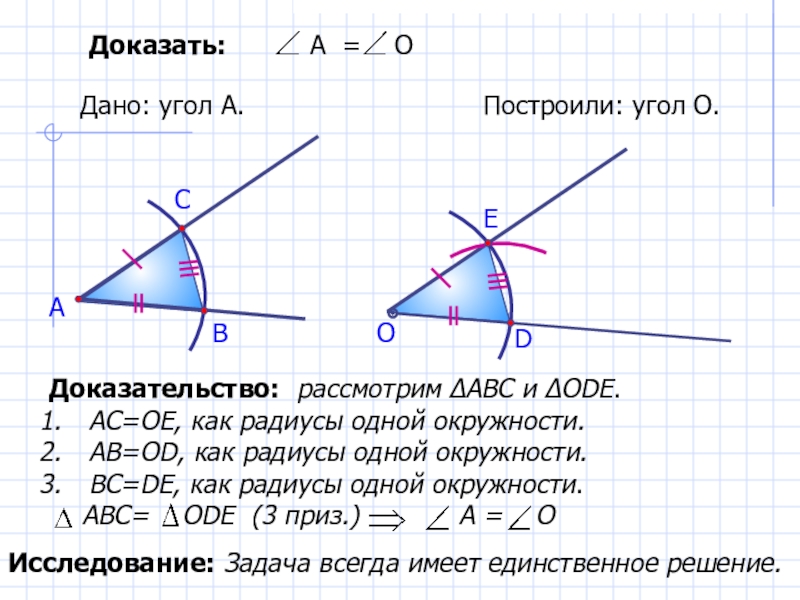
Дано: угол А.
А
Построили: угол О.
В
С
О
D
E
Доказательство: рассмотрим ΔАВС и ΔОDE.
АС=ОЕ, как радиусы
АВ=ОD, как радиусы одной окружности.
ВС=DE, как радиусы одной окружности.
АВС= ОDЕ (3 приз.) А = О
Доказать: А = О
Исследование: Задача всегда имеет единственное решение.
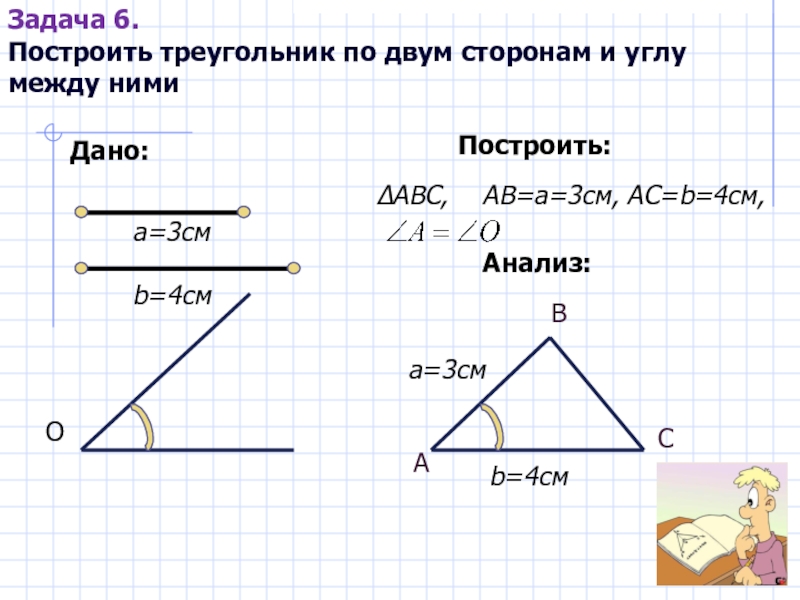
Слайд 20Задача 6.
Построить треугольник по двум сторонам и углу между ними
Дано:
а=3см
b=4см
О
Построить:
ΔАВС,
АВ=а=3см, АС=b=4см,
Анализ:
b=4см
а=3см
А
В
С
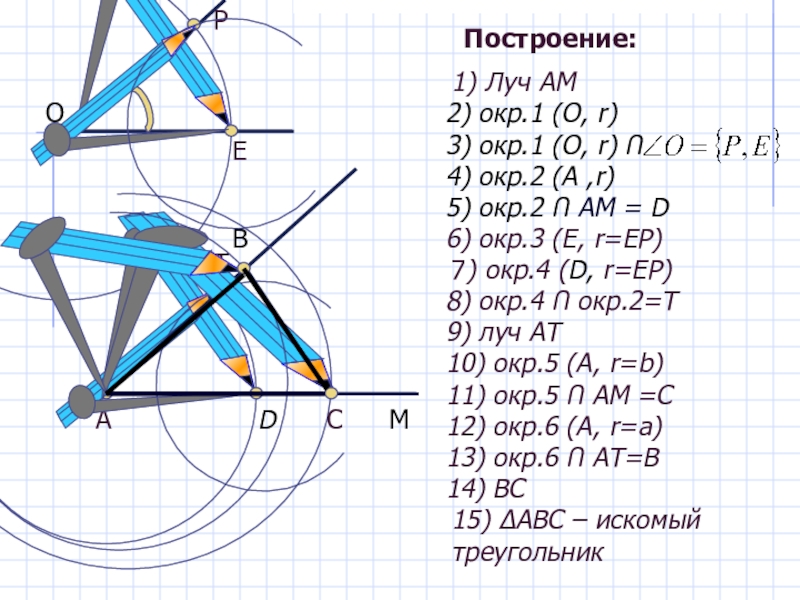
Слайд 21Построение:
1) Луч АМ
А
М
О
2) окр.1 (О, r)
3) окр.1 (О, r) Ո
Р
Е
4) окр.2 (А ,r)
5) окр.2 Ո АМ = D
D
6) окр.3 (Е, r=ЕР)
7) окр.4 (D, r=ЕР)
8) окр.4 Ո окр.2=Т
Т
9) луч АТ
10) окр.5 (А, r=b)
11) окр.5 Ո АМ =С
С
12) окр.6 (А, r=а)
13) окр.6 Ո АТ=В
В
14) ВС
15) ΔАВС – искомый треугольник
Слайд 22Доказательство:
В ΔАВС :
АВ=а=3см как радиусы одной окружности
АС=b=4см как радиусы одной окружности
Значит, треугольники равны по первому признаку
Исследование:
Задача всегда имеет единственное решение.
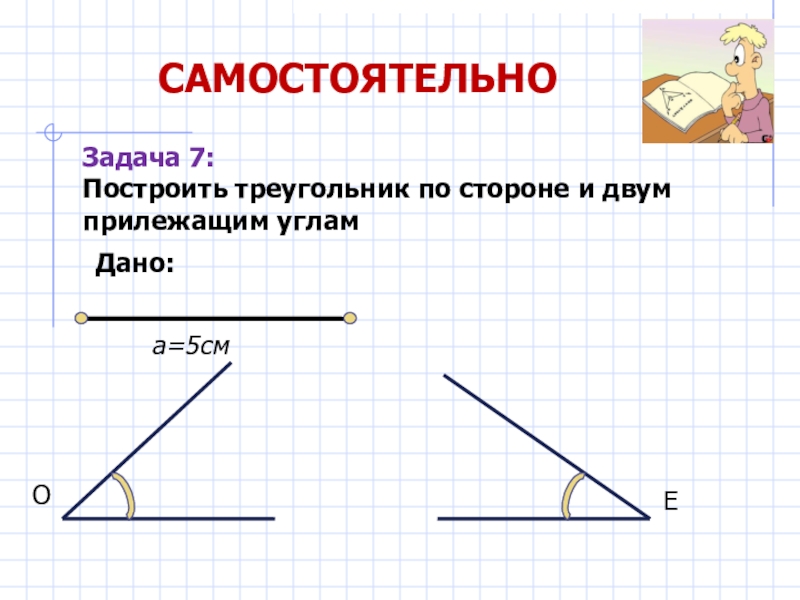
Слайд 23САМОСТОЯТЕЛЬНО
Задача 7:
Построить треугольник по стороне и двум прилежащим углам
Дано:
а=5см
О
Е
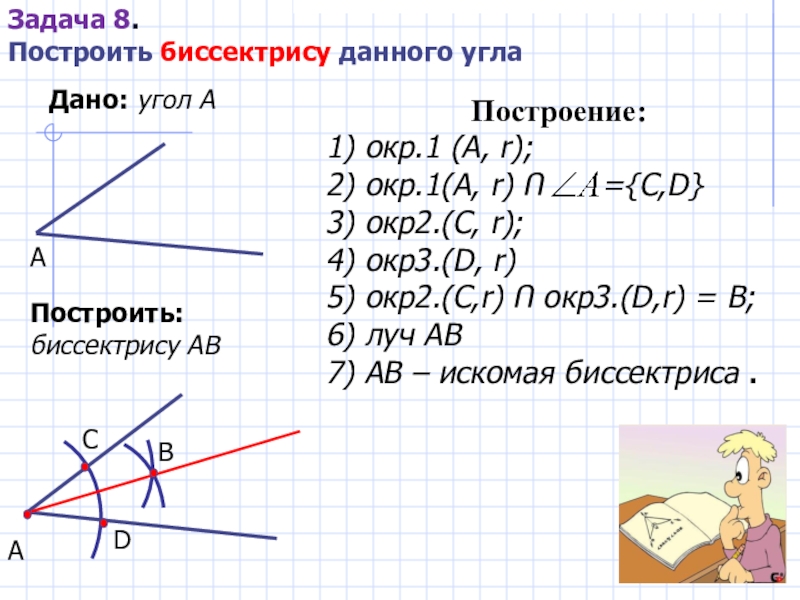
Слайд 24Дано: угол А
Построить: биссектрису АВ
Построение:
1) окр.1 (A, r);
2) окр.1(A, r) Ո
3) окр2.(C, r);
4) окр3.(D, r)
5) окр2.(C,r) Ո окр3.(D,r) = B;
6) луч AB
7) AB – искомая биссектриса .
А
D
C
B
Задача 8.
Построить биссектрису данного угла
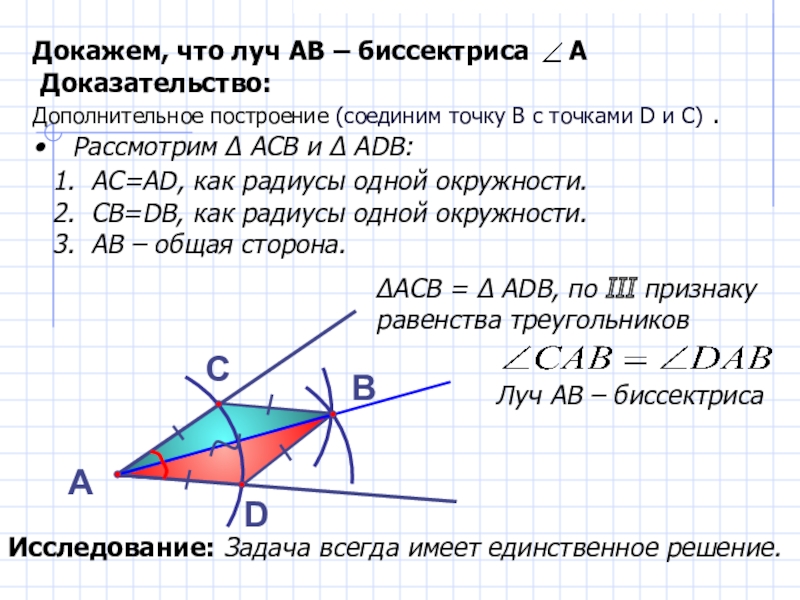
Слайд 25
Докажем, что луч АВ – биссектриса А
Доказательство:
Дополнительное
Рассмотрим ∆ АСВ и ∆ АDB:
А
В
С
D
АС=АD, как радиусы одной окружности.
СВ=DB, как радиусы одной окружности.
АВ – общая сторона.
∆АСВ = ∆ АDВ, по III признаку
равенства треугольников
Луч АВ – биссектриса
Исследование: Задача всегда имеет единственное решение.
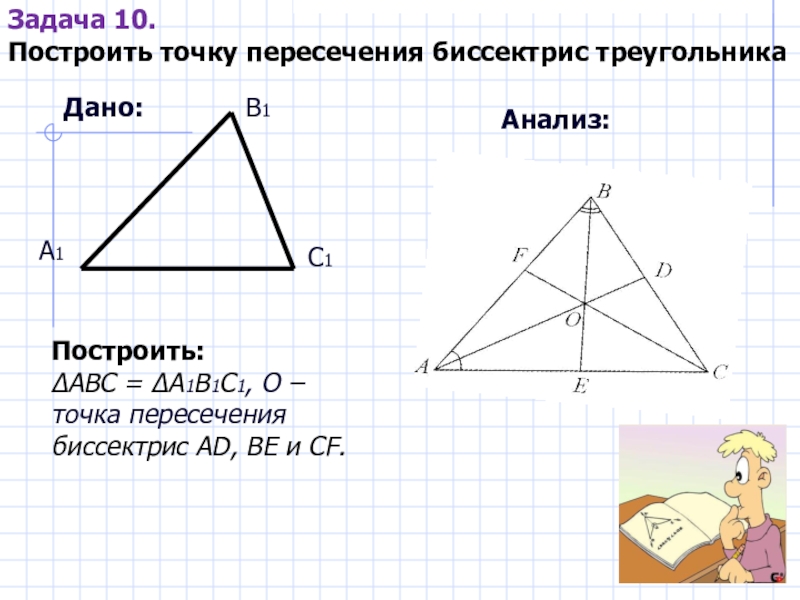
Слайд 28Задача 10.
Построить точку пересечения биссектрис треугольника
Дано:
А1
В1
С1
Построить:
ΔАВС = ΔА1В1С1, О –
Анализ:
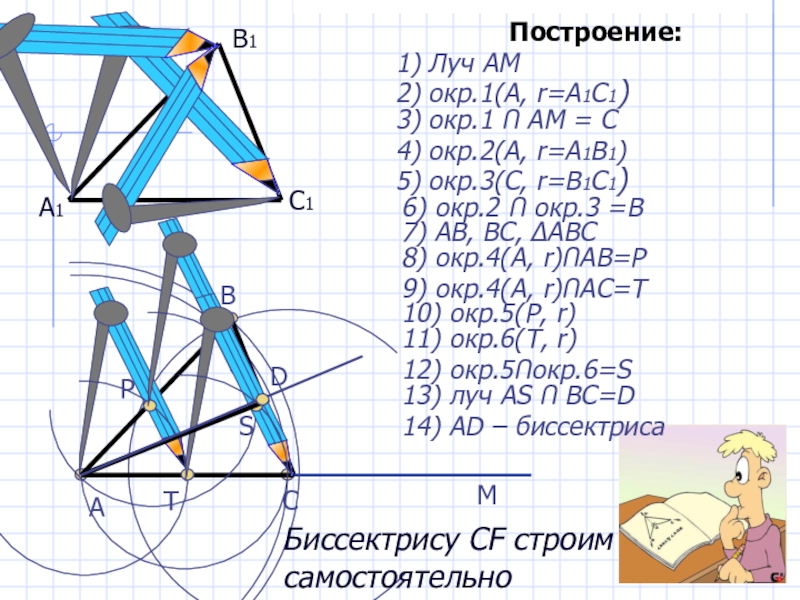
Слайд 29Дано:
А1
В1
С1
Построение:
1) Луч АМ
А
М
2) окр.1(А, r=А1С1)
С
3) окр.1 Ո АМ = С
4)
5) окр.3(С, r=В1С1)
6) окр.2 Ո окр.3 =В
В
7) АВ, ВС, ΔАВС
8) окр.4(А, r)ՈАВ=Р
Р
9) окр.4(А, r)ՈАС=Т
Т
10) окр.5(Р, r)
11) окр.6(Т, r)
12) окр.5Ոокр.6=S
S
13) луч АS Ո BC=D
14) AD – биссектриса
D
Биссектрису CF строим самостоятельно
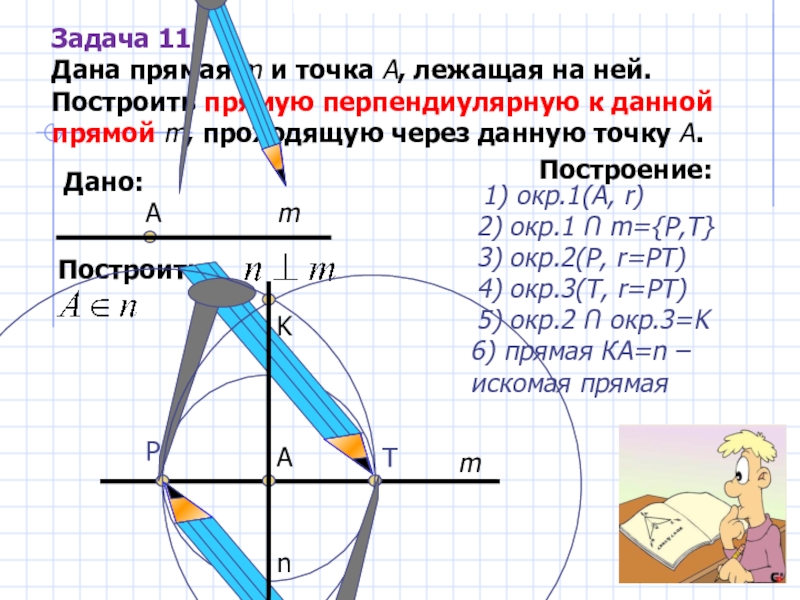
Слайд 30Задача 11.
Дана прямая m и точка A, лежащая на ней. Построить
Дано:
m
А
Построить:
Построение:
m
А
1) окр.1(А, r)
2) окр.1 Ո m={P,T}
P
T
3) окр.2(Р, r=PT)
4) окр.3(T, r=PT)
5) окр.2 Ո окр.3=K
K
6) прямая КА=n – искомая прямая
n
Слайд 31Построили:
m
n
А
P
Т
К
Доказательство:
Проведём отрезки РК и КТ
Рассмотрим ΔКРА и ΔКТА. У них:
КР=КТ =РТ
АР = АТ как радиусы одной окружности
АК – общая сторона
Значит, ΔКРА = ΔКТА по трём сторонам
Из равенства треугольников следует равенство соответствующих углов
А так как они смежные, то 180º:2=90º.
Значит,
Слайд 32Работа в паре
Учебник, задача №153
Даны прямая а и точка М, не
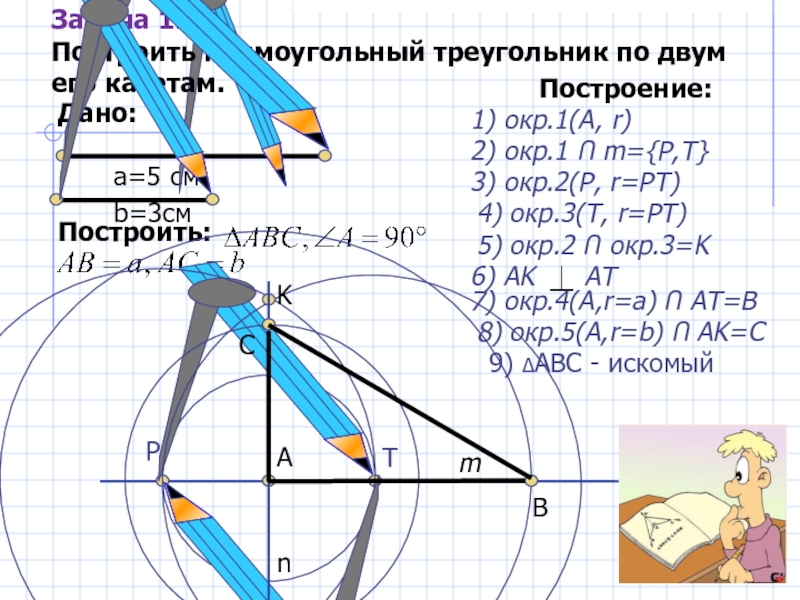
Слайд 33Дано:
b=3см
а=5 см
Построить:
Построение:
m
А
1) окр.1(А, r)
2) окр.1 Ո m={P,T}
P
T
3) окр.2(Р, r=PT)
4)
5) окр.2 Ո окр.3=K
K
6) AK AT
n
Задача 12.
Построить прямоугольный треугольник по двум его катетам.
7) окр.4(А,r=a) Ո AT=B
B
8) окр.5(А,r=b) Ո AK=C
C
9) ΔABC - искомый
Слайд 34Самостоятельная работа
Первый вариант
Построить прямоугольный треугольник по катету и гипотенузе
Второй вариант
Построить равнобедренный
Третий вариант
Построить прямоугольный треугольник по катету и острому углу
Слайд 351. Укажите, какое из указанных дальше построений можно выполнить с помощью
А) провести произвольную прямую;
Б) построить любой луч, который выходит из данной точки и проходит через другую данную точку;
В) отложить на данной прямой от данной на ней точки отрезок, который равен данному;
Г) каждое из перечисленных построений выполнить невозможно.
ТЕСТ
Слайд 362. Укажите, какое из приведенных дальше построений можно выполнить с помощью
А) построить окружность данного радиуса из центром в данной точке;
Б) построить точку, удаленную от двух данных точек на данное расстояние;
В) соединить отрезком две данные точки;
Г) поделить отрезок пополам.
ТЕСТ
Слайд 37ТЕСТ
3. Треугольник можно построить из трех отрезков, которые имеют длину:
А)
Б) 45 см; 46 см; 1 м;
В) 1 м; 1 м; 0,5 см;
Г) ни один из приведенных вариантов.
Слайд 384. Треугольник АВС можно построить, если:
А)
Б) АВ = 5 см, ВС
В)
Г) АВ = 6 см, ВС = 4 см.
ТЕСТ
Слайд 39ТЕСТ
5. Геометрическим местом точек плоскости, равноудаленных от одной точки, является:
А)
Б) квадрат;
В) круг;
Г) куб.
Слайд 406. Какую фигуру образуют все точки плоскости, которые расположены на расстоянии
А) окружность с центром М и радиусом 3 см;
Б) прямую, которая расположена на расстоянии 6 см от точки М;
В) окружность из центром М и радиусом 6 см;
Г) равносторонний треугольник из сторонами 6 см.
ТЕСТ
Слайд 41ТЕСТ
7. Геометрическим местом точек угла, равноудаленных от его сторон, является:
А)
Б) серединный перпендикуляр;
В) медиана;
Г) свой вариант ответа.
Слайд 42ТЕСТ
8. Какое из утверждений неправильное:
А) С помощью линейки можно отложить
Б) Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, которые имеют определенные свойства.
В) С помощью линейки можно провести произвольную прямую; прямую, которая проходит через одну или две данные точки.
Г) Циркулем можно описать окружность данного радиуса из центром в данной точке, а также отложить данный отрезок на данной прямой из данной точки.
Слайд 43ТЕСТ
9. Какую фигуру образуют все точки плоскости, которая расположена на расстоянии
А) прямую, которая расположена на расстоянии 4 м от данной прямой;
Б) две прямые параллельные данной, которые расположены на расстоянии 4 м от данной прямой;
В) равносторонний треугольник из стороной 4 м;
Г) окружность радиусом 4 м.
Слайд 44ТЕСТ
10. Какая из задач не является основной задачей на построение?
А) построение
Б) построение середины отрезка;
В) построение угла, равного данному
Г) построение прямоугольного треугольника по двум его катетам;