- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Треугольники
Содержание
- 1. Презентация по геометрии по теме Треугольники
- 2. Цели:Перед собой мы поставили следующие цели:Выяснить исторические
- 3. Исторические факты о треугольнике: 1. В одном
- 4. 2. Через 2000 лет в Древней Греции очень активно велось изучение его свойств
- 5. 3. Император Франции Наполеон свободное время посвящал занятиям математикой и, в частности, изучению свойств треугольников.
- 6. Что такое треугольник?Это самая простая замкнутая геометрическая
- 7. Равнобедренный треугольникЭто треугольник, в котором две стороны равны
- 8. Равносторонний треугольникПравильный (или равносторонний) треугольник — это правильный многоугольник с тремя сторонами, простейший
- 9. Свойства равнобедренных треугольников
- 10. AB = BC — боковые стороны; AC
- 11. Признаки равнобедренного треугольника:
- 12. Свойства равносторонних треугольников
- 13. 1) Все углы равностороннего треугольника равны по
- 14. Решение задач
- 15. 1. Задачи на равнобедренные треугольники
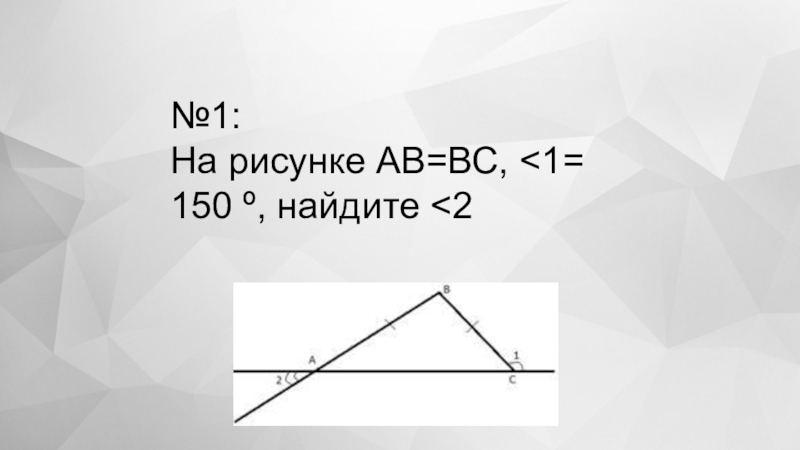
- 16. №1:На рисунке АВ=ВС,
- 17. 1)
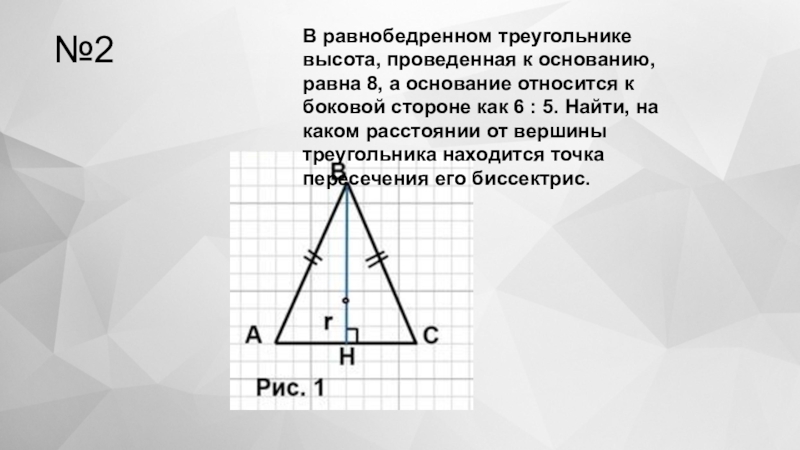
- 18. №2В равнобедренном треугольнике высота, проведенная к основанию,
- 19. Пусть дан равнобедренный треугольник АВС (рис. 1).1) Так
- 20. №3В равнобедренном треугольнике АВС проведена биссектриса АD.
- 21. Рассмотрим треугольник АВС – равнобедренный, АD –
- 22. 2. Задачи на равносторонние треугольники
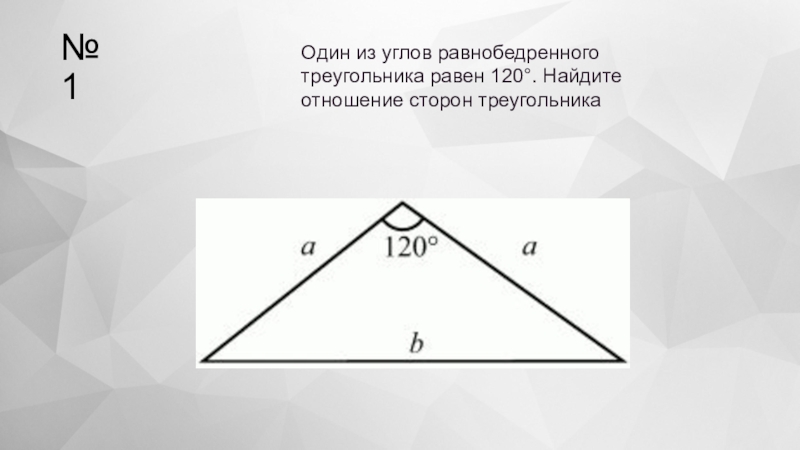
- 23. №1Один из углов равнобедренного треугольника равен 120°. Найдите отношение сторон треугольника
- 24. Решение. Обозначим основание треугольника через b, боковые
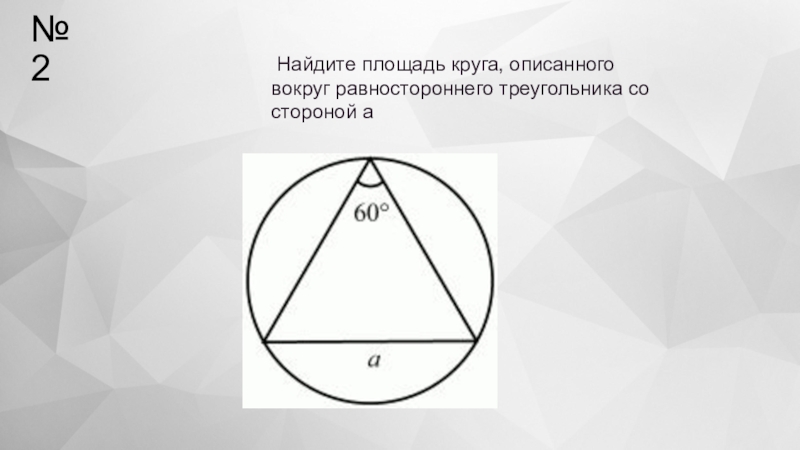
- 25. №2 Найдите площадь круга, описанного вокруг равностороннего треугольника со стороной а
- 26. Решение. Обозначим сторону треугольника через а. Тогда по теореме синусов имеем:Площадь круга:Ответ:
- 27. №3Основание равнобедренного треугольника равно 4√2, медиана боковой стороны равна 5. Найдите длину боковой стороны
- 28. Решение. Можно воспользоваться готовой формулой длины медианы:Обозначим
- 29. Использованные источники:wikipedia.comtreugolniki.ruinterneturok.rublog.tutoronline.ruhttps://stydopedia.ru/
Слайд 1Равнобедренные и равносторонние треугольники
Проект выполнили ученики 9 «Г» класса, МОУ Гимназия
Николай Свистов
Степан Демичев
Слайд 2Цели:
Перед собой мы поставили следующие цели:
Выяснить исторические факты о треугольнике
Определить, что
Изучить свойства.
Решить задачи.
Слайд 3Исторические факты о треугольнике:
1. В одном египетском папирусе 4000-летней давности
Слайд 53. Император Франции Наполеон свободное время посвящал занятиям математикой и, в
Слайд 6Что такое треугольник?
Это самая простая замкнутая геометрическая фигура, одна из первых,
Слайд 7Равнобедренный треугольник
Это треугольник, в котором две стороны равны между собой по длине.
Слайд 8Равносторонний треугольник
Правильный (или равносторонний) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны
Слайд 10AB = BC — боковые стороны; AC — основание равнобедренного
А
В
С
В равнобедренном треугольнике углы при основании равны.
О
AB = BC (равнобедренный треугольник),
AO = OC (BO — медиана),
BO — общая сторона тр. ABO и тр. CBO.
тр. ABO = тр. CBO по 3-му признаку.
Следовательно: тр. ABO = тр. CBO.
BO — биссектриса.
• в равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой;
• в равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
Слайд 11 Признаки равнобедренного треугольника: •
Слайд 131) Все углы равностороннего треугольника равны по 60º
3) Высота, медиана и биссектриса, проведённые к каждой
AK — высота, медиана и биссектриса, проведённые к стороне BC;
BF — высота, медиана и биссектриса, проведённые к стороне AC;
CD — высота, медиана и биссектриса, проведённые к стороне AB.
Длины всех трёх высот (медиан, биссектрис) равны между собой:
AK=BF=CD.
2)длины всех медиан, высот и биссектрис равны
Слайд 18№2
В равнобедренном треугольнике высота, проведенная к основанию, равна 8, а основание
Слайд 19Пусть дан равнобедренный треугольник АВС (рис. 1).
1) Так как АС : ВС
Так как точка Н – середина АС (по свойству равнобедренного треугольника), то НС = 1/2 АС = 1/2 · 6х = 3х.
2) Из треугольника ВНС – прямоугольного по теореме Пифагора
ВС2 = ВН2 + НС2;
(5х)2 = 82 + (3х)2;
16х2 = 64;
х2 = 4;
х = 2, тогда
АС = 6х = 6 · 2 = 12 и
ВС = 5х = 5 · 2 = 10.
3) Так как точка пересечения биссектрис треугольника является центром вписанной в него окружности, то ОН = r . Радиус вписанной в треугольник АВС окружности найдем по формуле
S = pr;
r = S/p.
4) SABC = 1/2 · (AC · BH); SABC = 1/2 · (12 · 8) = 48;
p = 1/2 · (AB + BC + AC); p = 1/2 · (10 + 10 + 12) = 16, тогда ОН = r = 48/16 = 3.
Отсюда ВО = ВН – ОН; ВО = 8 – 3 = 5.
Ответ: 5.
Слайд 20№3
В равнобедренном треугольнике АВС проведена биссектриса АD. Площади треугольников ABD и
Слайд 21Рассмотрим треугольник АВС – равнобедренный, АD – биссектриса угла А (рис. 2).
1)
SBAD = 1/2 · AB · AD · sin α; SDAC = 1/2 · AC · AD · sin α.
2) Найдем отношение площадей:
SBAD/SDAC = (1/2 · AB · AD · sin α) / (1/2 · AC · AD · sin α) = AB/AC.
Так как SBAD = 10, SDAC = 12, то 10/12 = АВ/АС;
АВ/АС = 5/6, тогда пусть АВ = 5х и АС = 6х.
АН = 1/2 АС = 1/2 · 6х = 3х.
3) Из треугольника АВН – прямоугольного по теореме Пифагора АВ2 = АН2 + ВН2;
25х2 = ВН2 + 9х2;
ВН = 4х.
4) SAВС = 1/2 · AС · ВН; SAВC = 1/2 · 6х · 4х = 12х2.
Так как SAВС = SBAD + SDAC = 10 + 12 = 22, тогда 22 = 12х2;
х2 = 11/6; ВН2 = 16х2 = 16 · 11/6 = 1/3 · 8 · 11 = 88/3.
5) Площадь квадрата равна ВН2 = 88/3; 3 · 88/3 = 88.
Ответ: 88.
Слайд 23№1
Один из углов равнобедренного треугольника равен 120°. Найдите отношение сторон треугольника
Слайд 24Решение. Обозначим основание треугольника через b, боковые стороны через а (см.
Тогда отношения сторон треугольника а: а: в = 1:1:?3.
Ответ: 1:1:√3.
Слайд 26Решение. Обозначим сторону треугольника через а. Тогда по теореме синусов имеем:
Площадь
Ответ:
Слайд 27№3
Основание равнобедренного треугольника равно 4√2, медиана боковой стороны равна 5. Найдите
Слайд 28Решение. Можно воспользоваться готовой формулой длины медианы:
Обозначим АВ через 2х, тотда
Имеем:
АВ = ВС = 6.