и решению задач
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Средняя линия треугольника
Содержание
- 1. Презентация по геометрии по теме Средняя линия треугольника
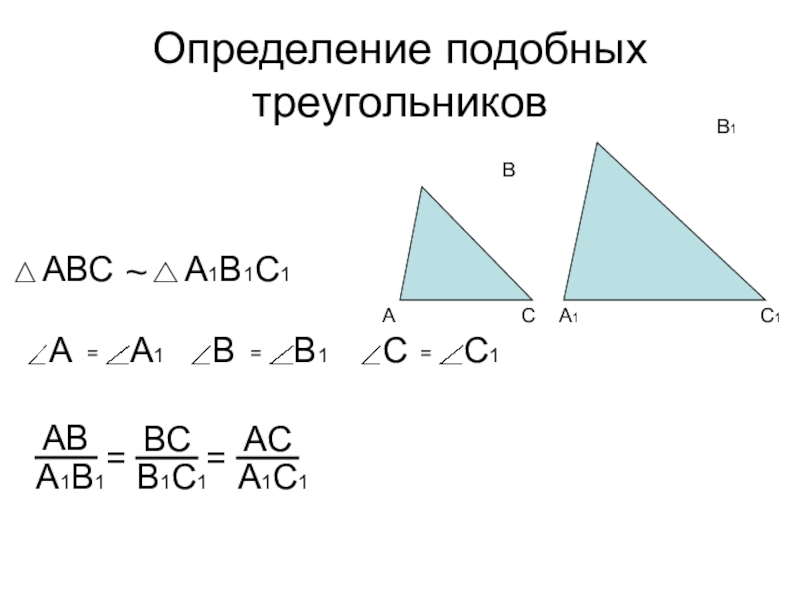
- 2. Определение подобных треугольников~==
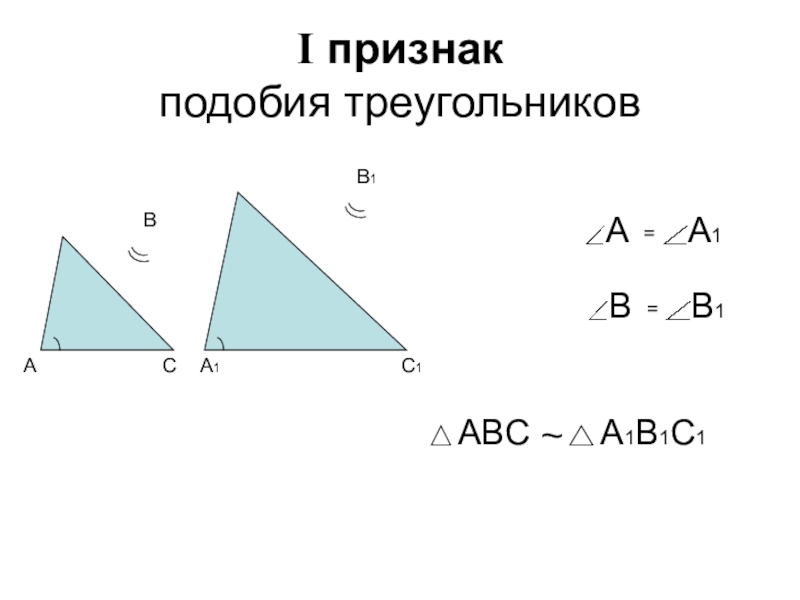
- 3. I признак подобия треугольников~
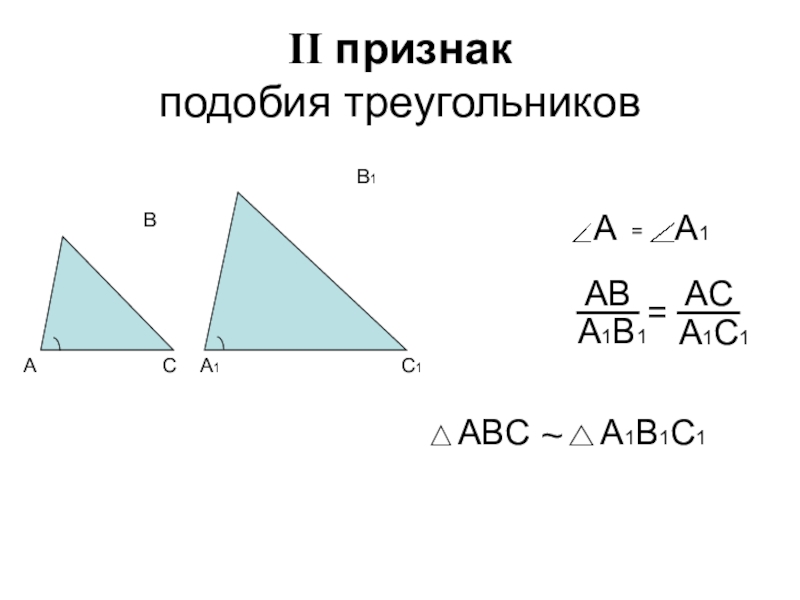
- 4. II признак подобия треугольников=~
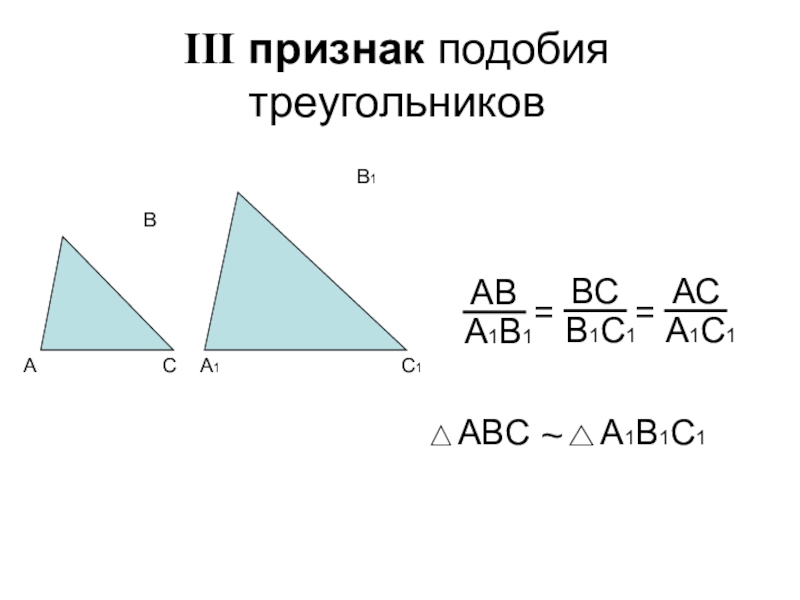
- 5. III признак подобия треугольников~==
- 6. ОпределениеACBMNAM=MB, BN=NCMN – средняя линия
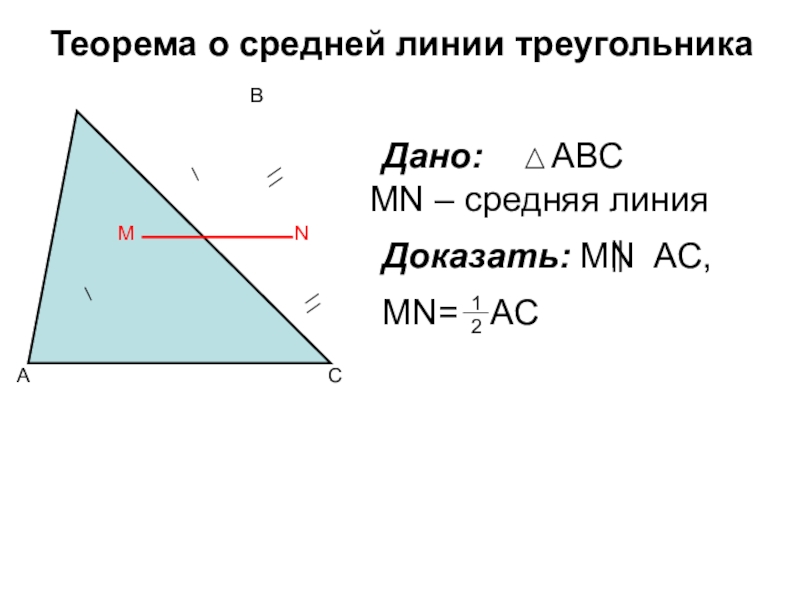
- 7. Теорема о средней линии треугольникаДано: MN – средняя линияДоказать: MN AC, MN=12AC
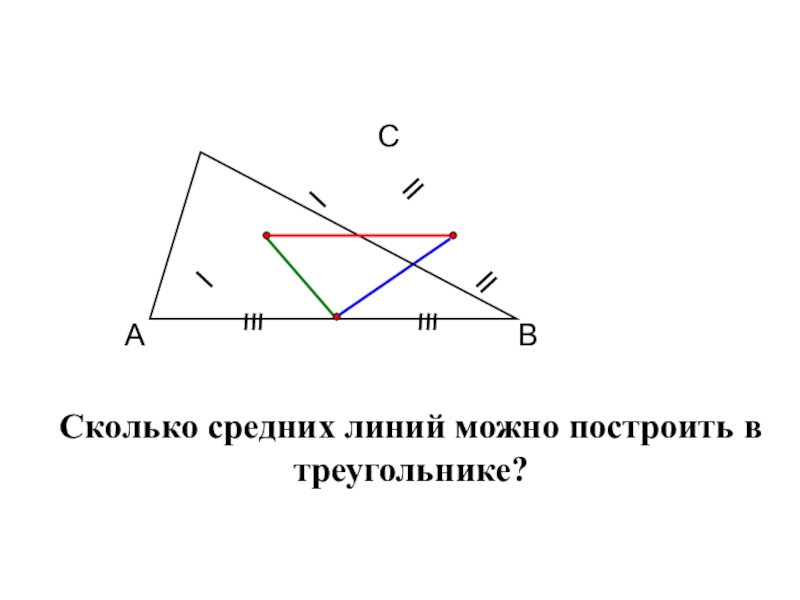
- 8. АСВСколько средних линий можно построить в треугольнике?
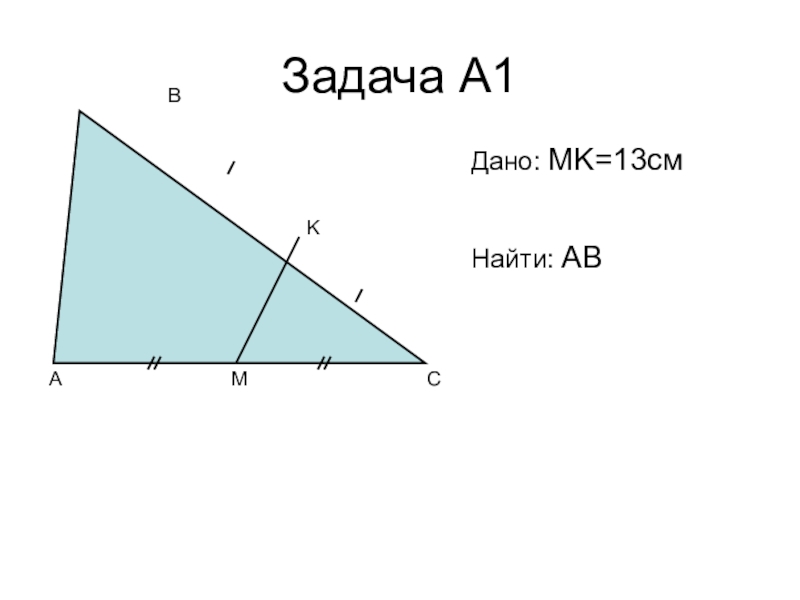
- 9. Задача А1ACBMKДано: MK=13см Найти: AB
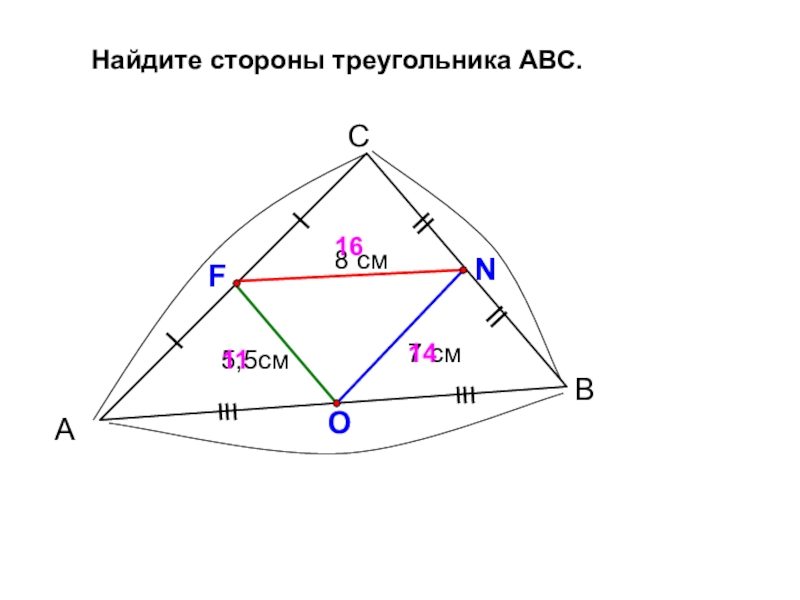
- 10. АСВ7 смFNO14Найдите стороны треугольника АВС.8 см5,5см1611
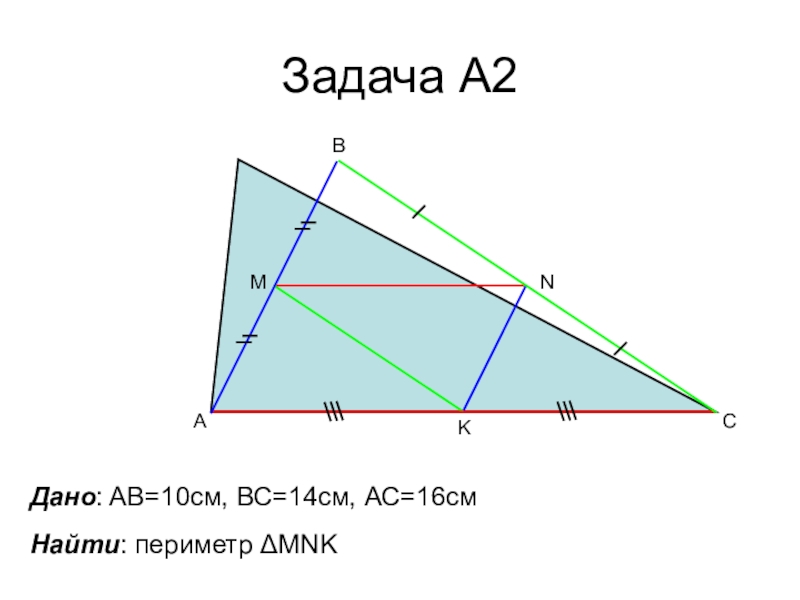
- 11. Задача А2ABCMNKДано: AB=10cм, ВС=14см, АС=16смНайти: периметр ΔMNK
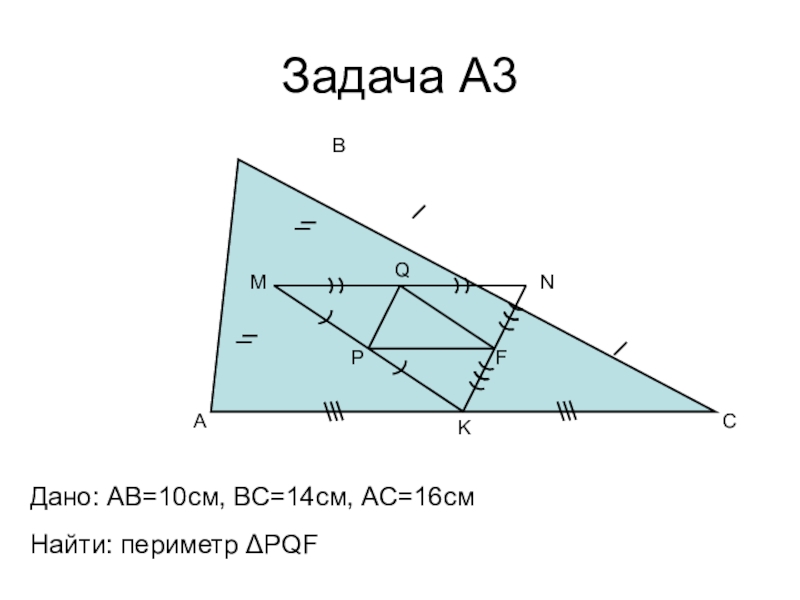
- 12. Задача А3ABCMNKPQFДано: AB=10cм, ВС=14см, АС=16смНайти: периметр ΔPQF
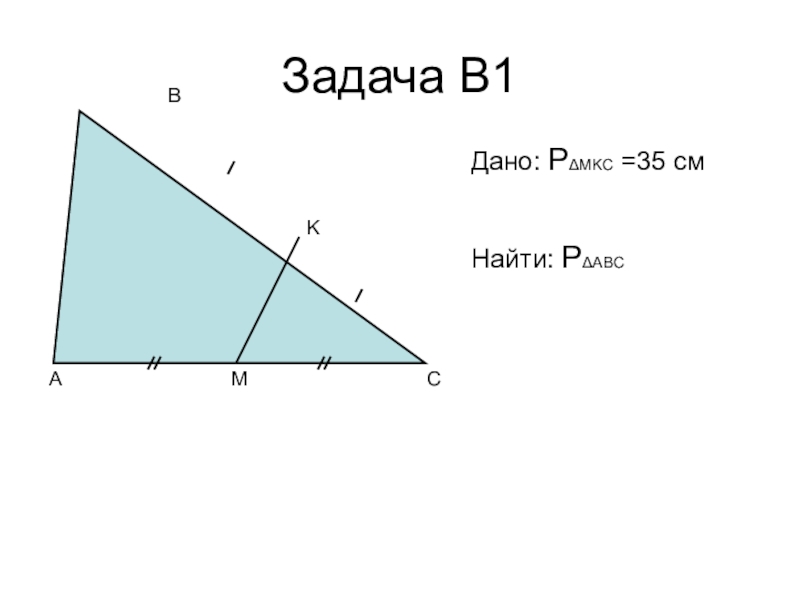
- 13. Задача В1ACBMKДано: PΔMKC =35 см Найти: PΔABC
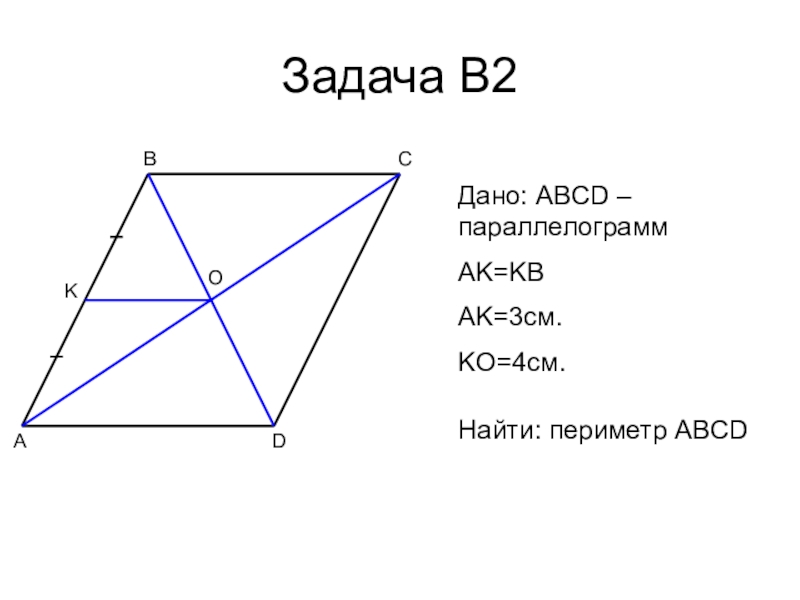
- 14. Задача В2ABCDOKДано: ABCD – параллелограммAK=KBAK=3см.KO=4см.Найти: периметр ABCD
- 15. Задача С1ABCDMNKДано: ABCD – параллелограммAC=10см, BD=6смK, L,
- 16. Задача С2ABCDMNKДано: ABCD – четырёхугольникK, L, M,
- 17. АСВСвойство медиан треугольника. Медианы треугольника пересекаются
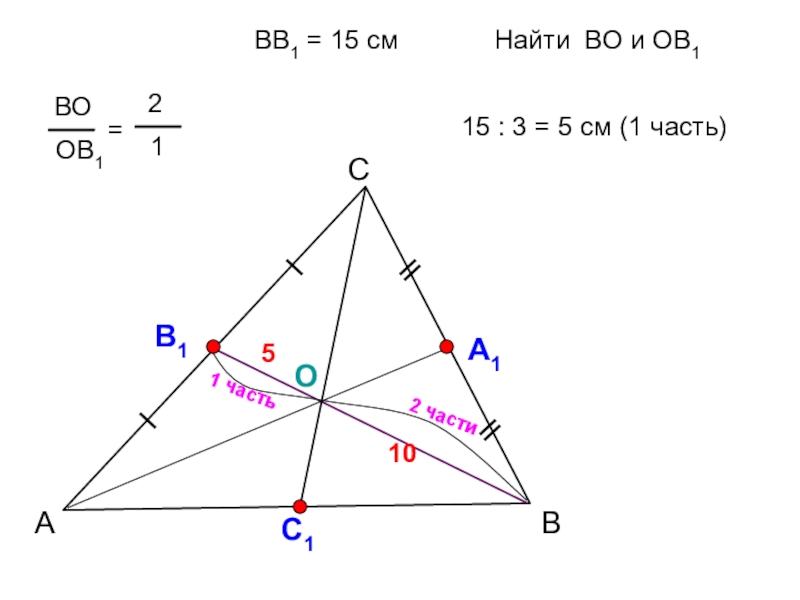
- 18. АСВА1ОС1ВВ1 = 15 смНайти ВО и ОВ1 15 : 3 = 5 см (1 часть)105
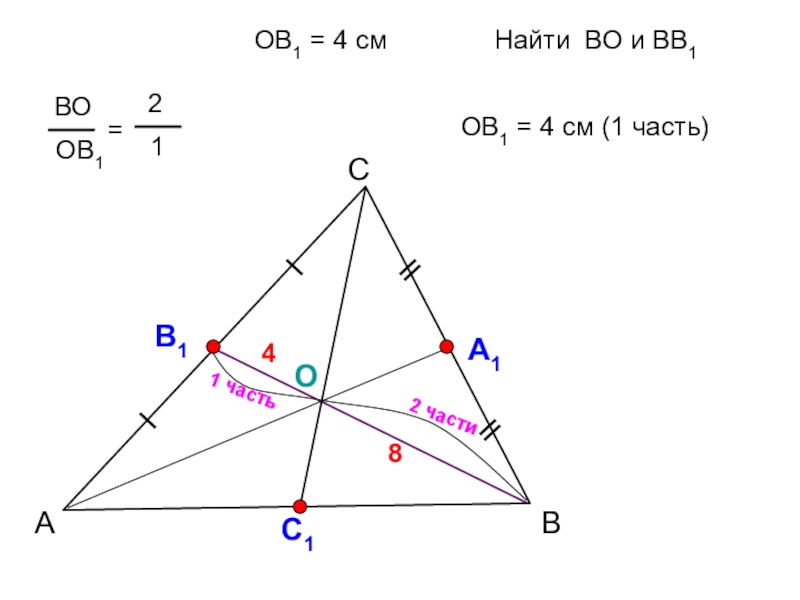
- 19. АСВ А1ОС1ОВ1 = 4 смНайти ВО и ВВ1 ОВ1 = 4 см (1 часть)84
- 20. Итог Отрезок, соединяющий середины двух сторон треугольника,
- 21. Домашнее задание
Определение подобных треугольников~==
Слайд 1Урок
Решение задач по теме «Средняя линия треугольника»
Применение подобия к доказательству теорем
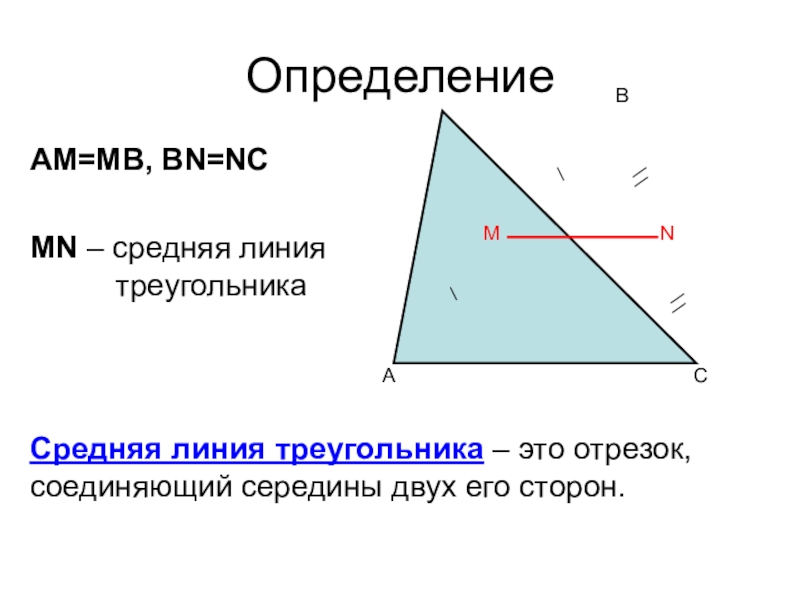
Слайд 6Определение
A
C
B
M
N
AM=MB, BN=NC
MN – средняя линия
треугольника
Средняя
линия треугольника – это отрезок, соединяющий середины двух его сторон.
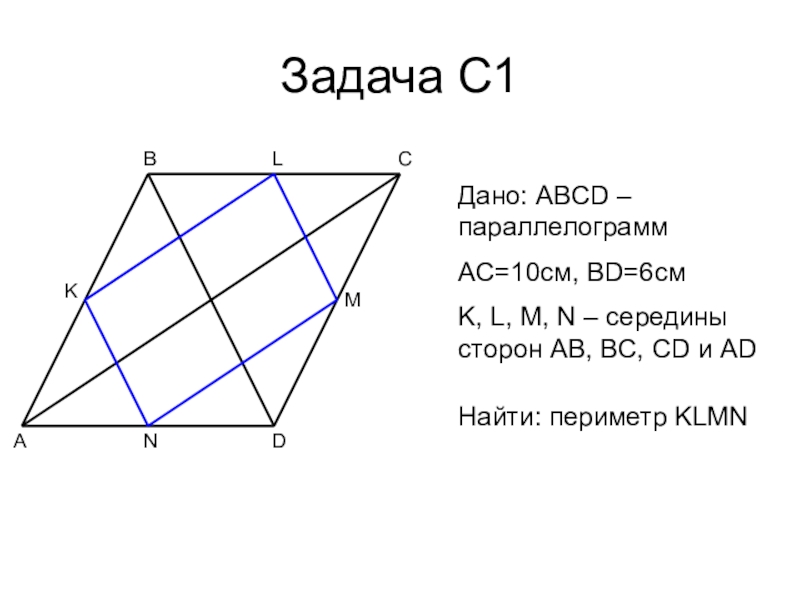
Слайд 15Задача С1
A
B
C
D
M
N
K
Дано: ABCD – параллелограмм
AC=10см, BD=6см
K, L, M, N – середины
сторон AB, BC, CD и AD
Найти: периметр KLMN
Найти: периметр KLMN
L
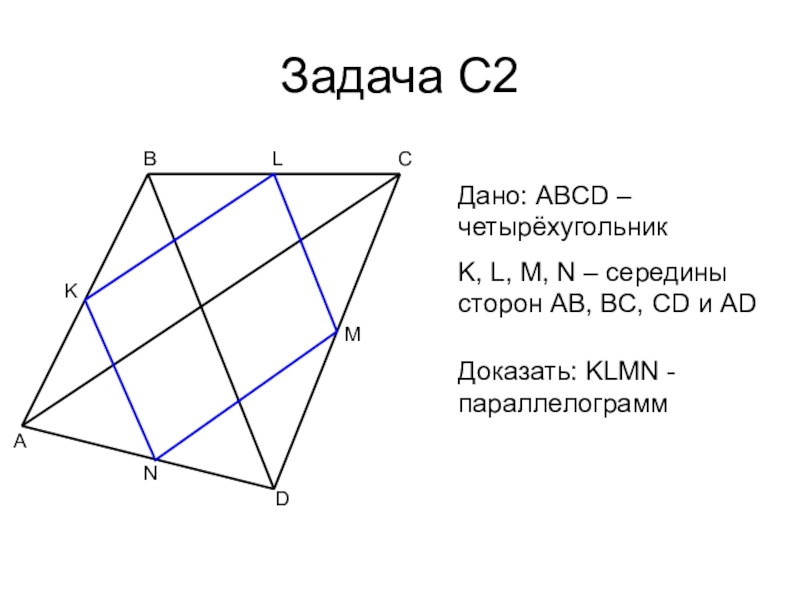
Слайд 16Задача С2
A
B
C
D
M
N
K
Дано: ABCD – четырёхугольник
K, L, M, N – середины сторон
AB, BC, CD и AD
Доказать: KLMN - параллелограмм
Доказать: KLMN - параллелограмм
L
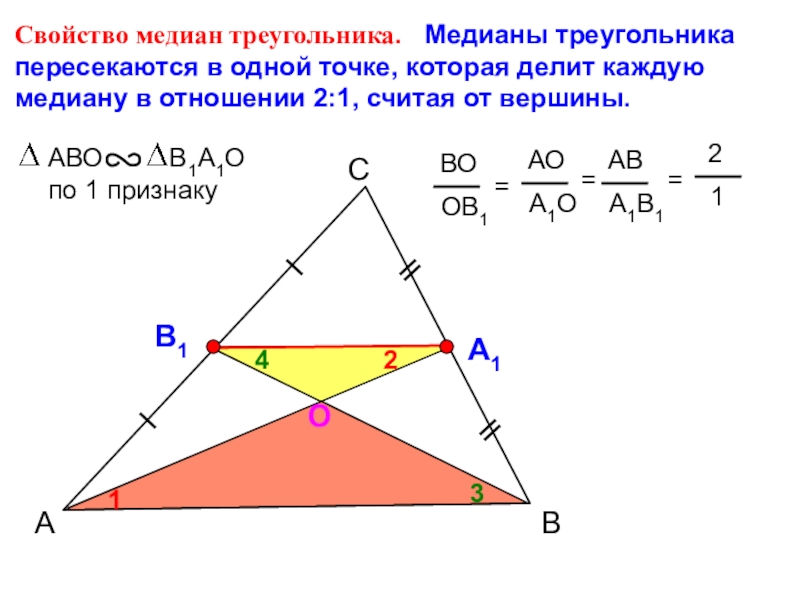
Слайд 17
А
С
В
Свойство медиан треугольника. Медианы треугольника пересекаются в одной точке, которая
делит каждую медиану в отношении 2:1, считая от вершины.
АВ
А1В1
Слайд 20Итог
Отрезок, соединяющий середины двух сторон треугольника, называется…
1.
Средняя линия треугольника параллельна
одной из его сторон и равна
2.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении
3.
средней линией треугольника.
половине этой стороны.
2 : 1, считая от вершины.