Актуализация знаний. Повторение теоретического материала.
2. Этап постановки учебной задачи
3.Из истории математики
4. Этап решения учебной задачи – Исследование свойств прямоугольного треугольника и их доказательство (Работа в группах), анализ условия задачи, моделирование выявленных отношений.
5. Этап решения учебной задачи – апробация сконструированной модели для решения конкретно-практических задач. Закрепление материала.
6. Этап решения частных задач.
7. Этап уточнения и конкретизации открытого способа действия.
8.Рефлексия. Подведение итогов. Домашнее задание.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Прямоугольный треугольник и некоторые свойства (7 класс)
Содержание
- 1. Презентация по геометрии по теме Прямоугольный треугольник и некоторые свойства (7 класс)
- 2. ТреугольникГеометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых отрезками, называется треугольником
- 3. Треугольники бываютРавносторонниеРавнобедренныеРавнобедренные РазносторонниеОстроугольныеТупоугольныеПрямоугольные
- 4. Если один из углов треугольника прямой, то треугольник называется900прямоугольным
- 5. Если все три угла треугольника острые, то треугольник называетсяостроугольным
- 6. Если один из углов треугольника тупой, то треугольник называется> 900тупоугольным.
- 7. Треугольник, все стороны которого равны, называетсяравносторонним.
- 8. Треугольник, у которого две стороны равны, называетсяравнобедренным.
- 9. Треугольник, у которого все стороны разные, называетсяразносторонним.
- 10. И ЕГО НЕКОТОРЫЕ СВОЙСТВА
- 11. Закрепить свойства прямоугольных треугольниковдоказать ихнаучиться применять на практике при решении задач Цели урока:
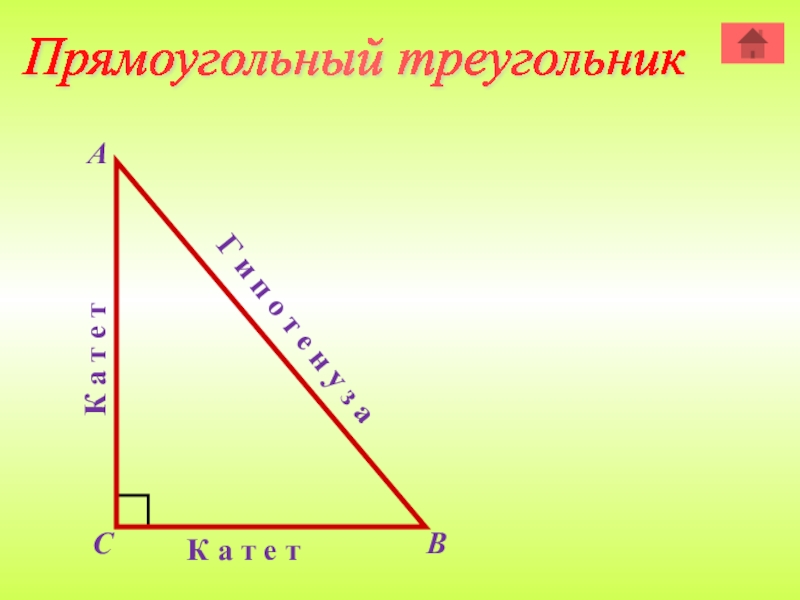
- 12. Прямоугольный треугольник АВСК а т е тК
- 13. Термин «гипотенуза» происходит от греческого слова «hypoteinusa»
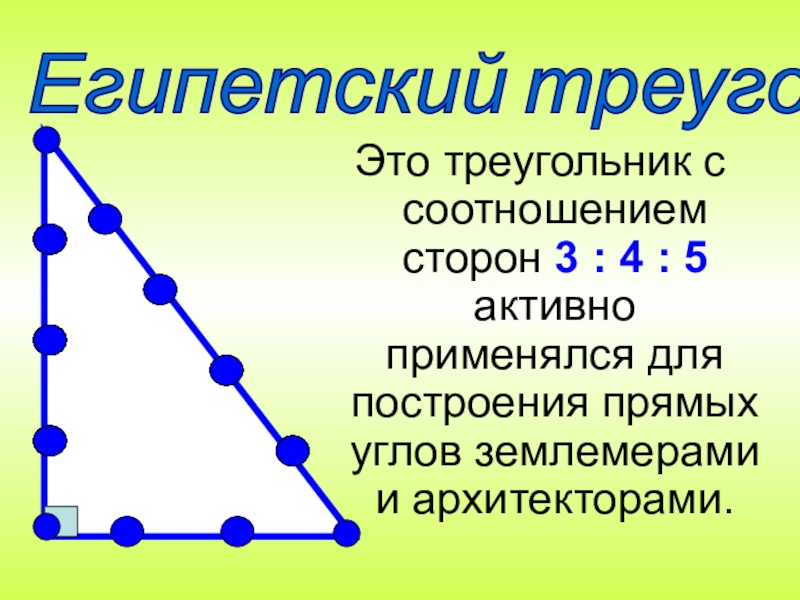
- 14. Это треугольник с соотношением сторон 3 :
- 15. Исследовательская работаЗадание №1: Чему равна сумма двух
- 16. Сумма двух острых углов прямоугольного треугольника равна
- 17. Катет прямоугольного треугольника, лежащий против угла в
- 18. Если катет прямоугольного треугольника равен половине гипотенузы,
- 19. Найдите углы равнобедренного прямоугольного треугольникаОтвет: 90°,45°, 45°.Задача
- 20. Доказать: Задача Доказательство следует из свойства 2
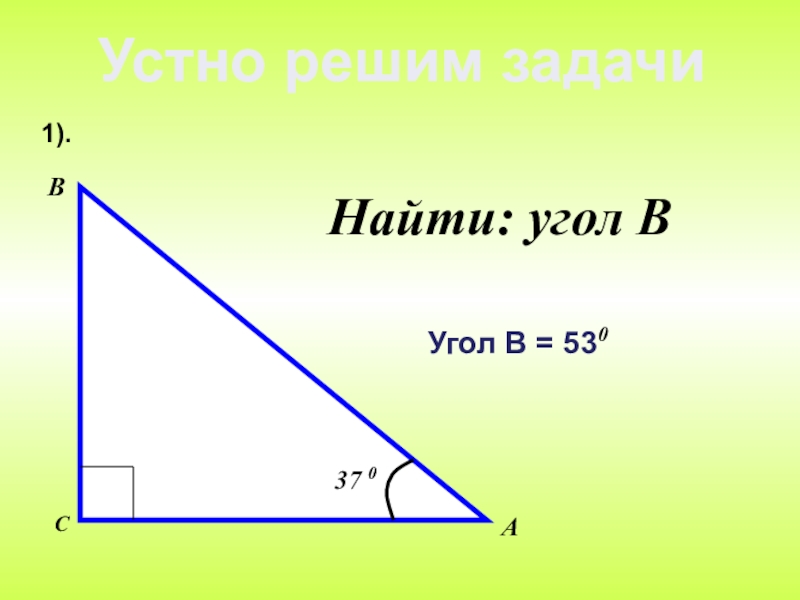
- 21. Найти: угол ВУстно решим задачиУгол В = 530 1).
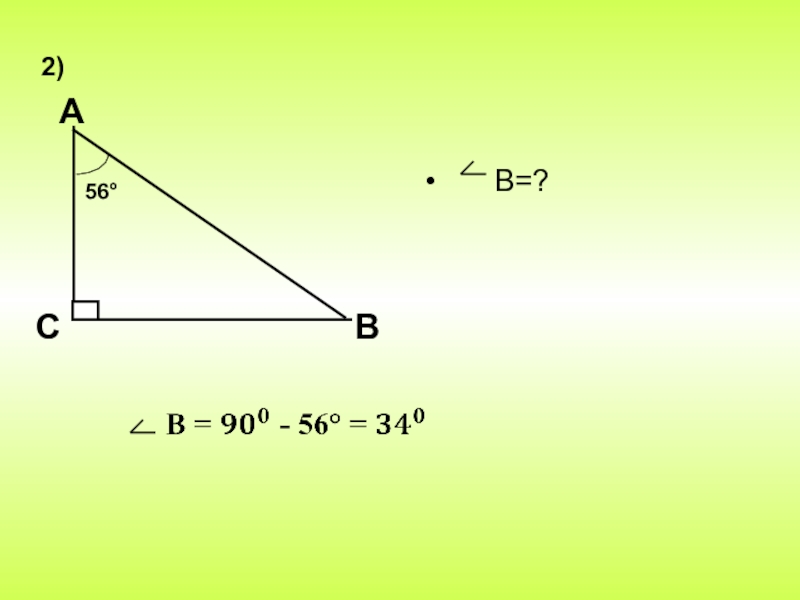
- 22. В=? А2)
- 23. САВ=?РR4). Р=? R=?АВ=8 Р=300 R=600
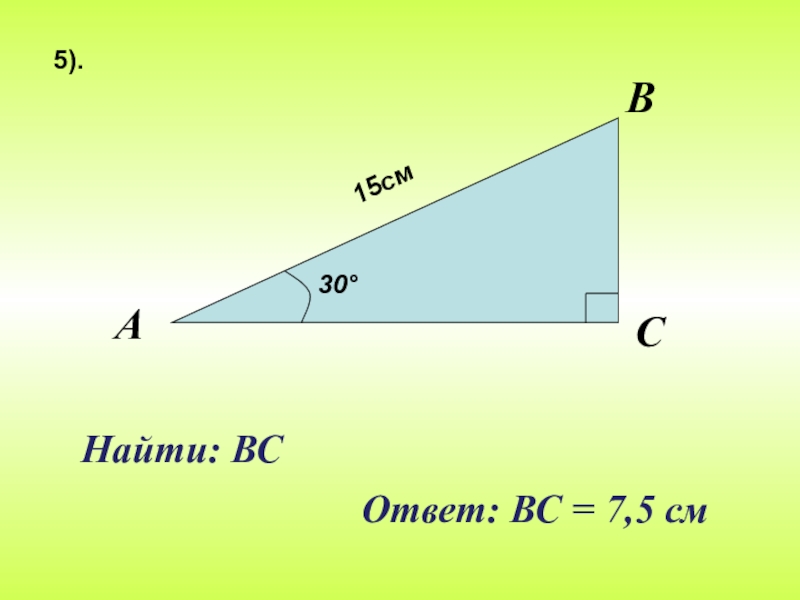
- 24. Найти: ВС5).Ответ: ВС = 7,5 см
- 25. Физминутка Раз хлопок руки вверх или внизДва хлопка сели или встали
- 26. Найти: Угол САВ1).70 0Ответ: 50 0Углы СВD
- 27. Найти: углы В, А, DСВ.Доказать: Δ АDС
- 28. Задание 1: Тест 1. Прямоугольным называется
- 29. 3. Стороны прямоугольного треугольника, образующие прямой угол,
- 30. 5. В треугольнике MNK гипотенуза KN равна
- 31. Ответы задания №3 1, 3, 5, 6, 8,
- 32. -Сумма двух острых углов прямоугольного треугольника равна
- 33. Я всё понял и могу доказать все
- 34. Итог самостоятельной работы: Всего верно решенных задач
- 35. №255, №256 Домашнее задание:
- 36. спасибо за урок!
ТреугольникГеометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых отрезками, называется треугольником
Слайд 2Треугольник
Геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой
и соединённых отрезками, называется треугольником
Слайд 3Треугольники
бывают
Равносторонние
РавнобедренныеРавнобедренные
Разносторонние
Остроугольные
Тупоугольные
Прямоугольные
Слайд 11Закрепить свойства прямоугольных треугольников
доказать их
научиться применять на практике при решении задач
Цели урока:
Слайд 13Термин «гипотенуза» происходит от греческого слова «hypoteinusa» (ипотейнуоза), обозначающее
«тянущаяся над чем-либо»,
«стягивающая».
Термин «катет» происходит от греческого слова «катетос», которое означало отвес, перпендикуляр
Термин «катет» происходит от греческого слова «катетос», которое означало отвес, перпендикуляр
Слайд 14Это треугольник с соотношением сторон 3 : 4 : 5 активно
применялся для построения прямых углов землемерами и архитекторами.
Египетский треугольник
Слайд 15Исследовательская работа
Задание №1: Чему равна сумма двух острых углов в прямоугольном
треугольнике?
Задание №2:Какая взаимосвязь между сторонами прямоугольного треугольника, у которого один из острых углов равен 30 градусов?
Задание №3:Какая особенность у прямоугольных треугольников, в которых один из катетов равен половине гипотенузы?
Задание №4: Докажите, что
Задание №5: Найдите углы равнобедренного прямоугольного треугольника
Задание №2:Какая взаимосвязь между сторонами прямоугольного треугольника, у которого один из острых углов равен 30 градусов?
Задание №3:Какая особенность у прямоугольных треугольников, в которых один из катетов равен половине гипотенузы?
Задание №4: Докажите, что
Задание №5: Найдите углы равнобедренного прямоугольного треугольника
Слайд 16Сумма двух острых углов прямоугольного треугольника равна 90°
Доказательство:
Сумма углов треугольника равна
180° , а прямой угол равен 90° , поэтому сумма двух острых углов прямоугольного треугольника равна 90° .
Свойство 1
ΔABC – прямоугольный, ∠С – прямой.
По теореме о сумме углов треугольника:
∠A+ ∠B + ∠C = 180º. Отсюда
∠A+ ∠B = 180º - ∠C = 90º,
что и требовалось доказать
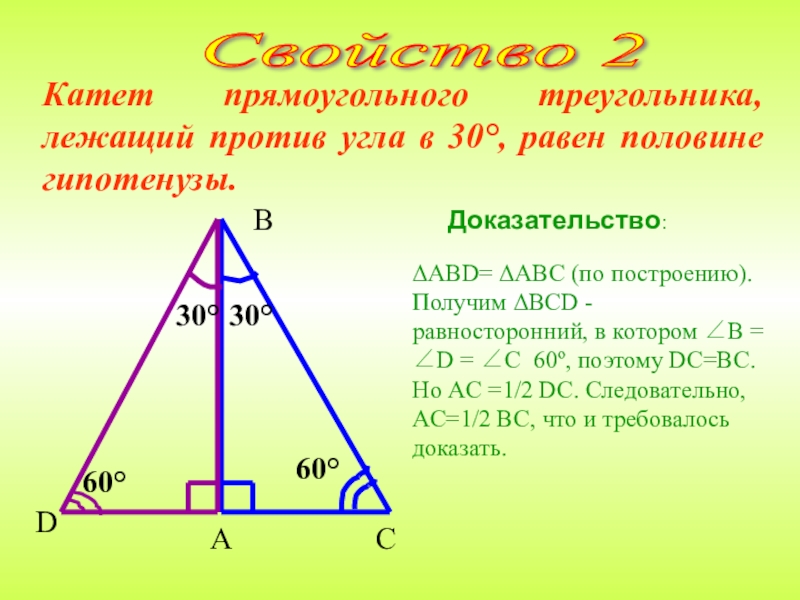
Слайд 17Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Свойство
2
С
В
А
30°
60°
Доказательство:
ΔАВD= ΔАBС (по построению).
Получим ΔBСD - равносторонний, в котором ∠B = ∠D = ∠С 60º, поэтому DC=BC. Но AC =1/2 DC. Следовательно, AC=1/2 BC, что и требовалось доказать.
Слайд 18
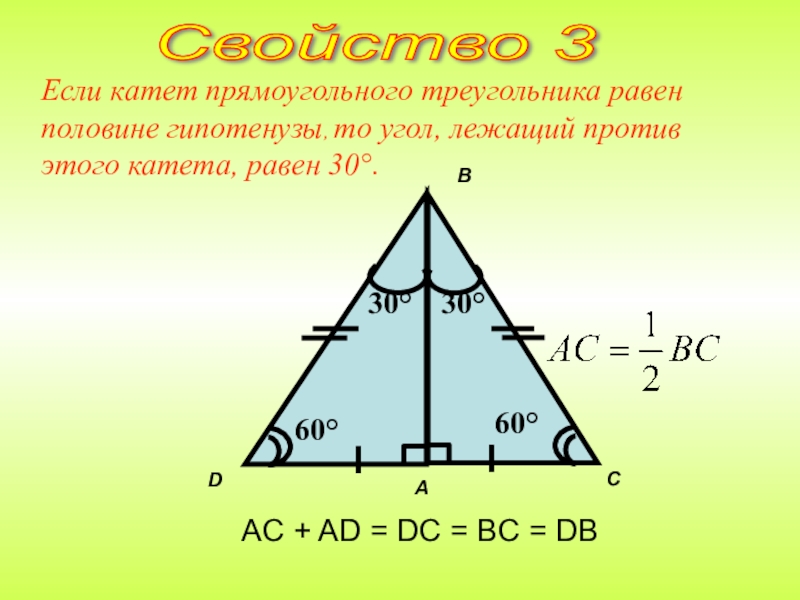
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против
этого катета, равен 30°.
Свойство 3
AC + AD = DC = BC = DB
30°
60°
30°
60°
Слайд 19Найдите углы равнобедренного прямоугольного треугольника
Ответ: 90°,45°, 45°.
Задача
Сумма двух острых углов
прямоугольного треугольника равна 90°, т.к. треугольник равнобедренный, острые углы будут равны по 45°
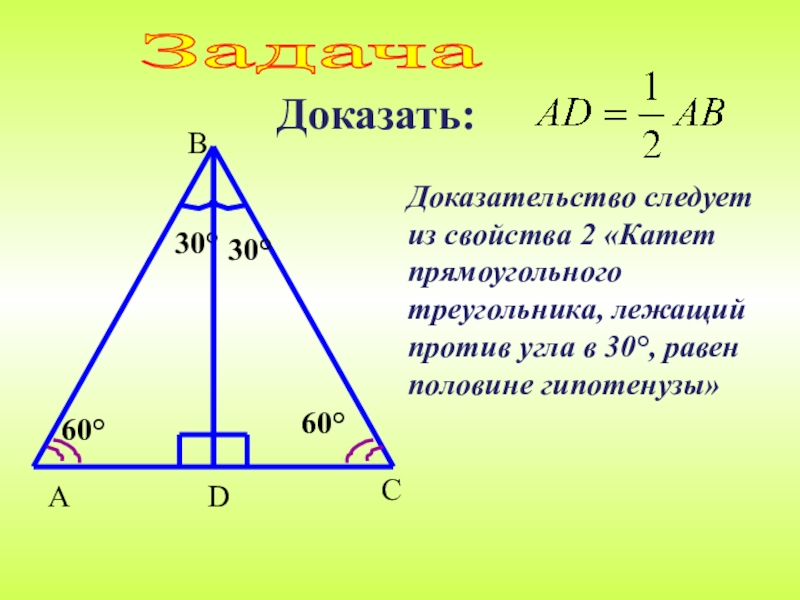
Слайд 20Доказать:
Задача
Доказательство следует из свойства 2 «Катет прямоугольного треугольника, лежащий
против угла в 30°, равен половине гипотенузы»
А
D
В
С
60°
60°
Слайд 26
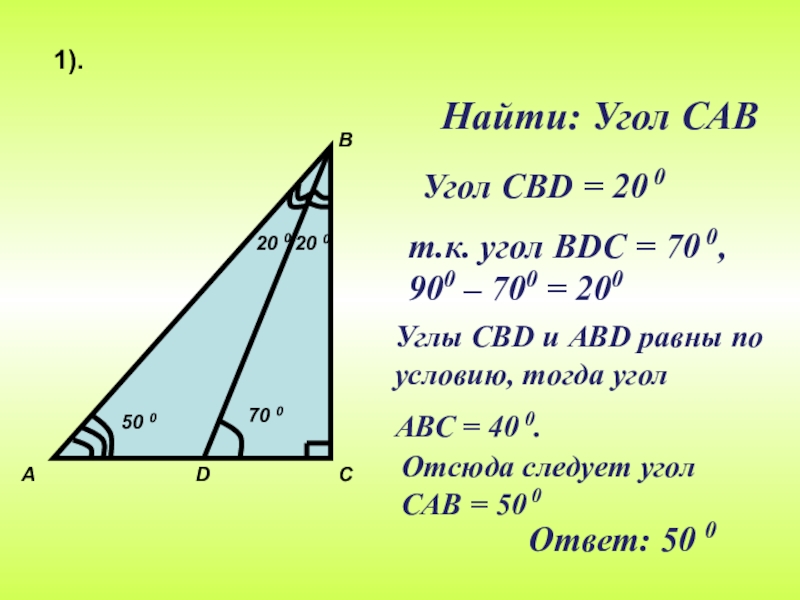
Найти: Угол САВ
1).
70 0
Ответ: 50 0
Углы СВD и ABD равны по
условию, тогда угол
АВС = 40 0.
АВС = 40 0.
Угол СВD = 20 0
т.к. угол ВDС = 70 0,
900 – 700 = 200
Отсюда следует угол САВ = 50 0
20 0
20 0
50 0
Слайд 27
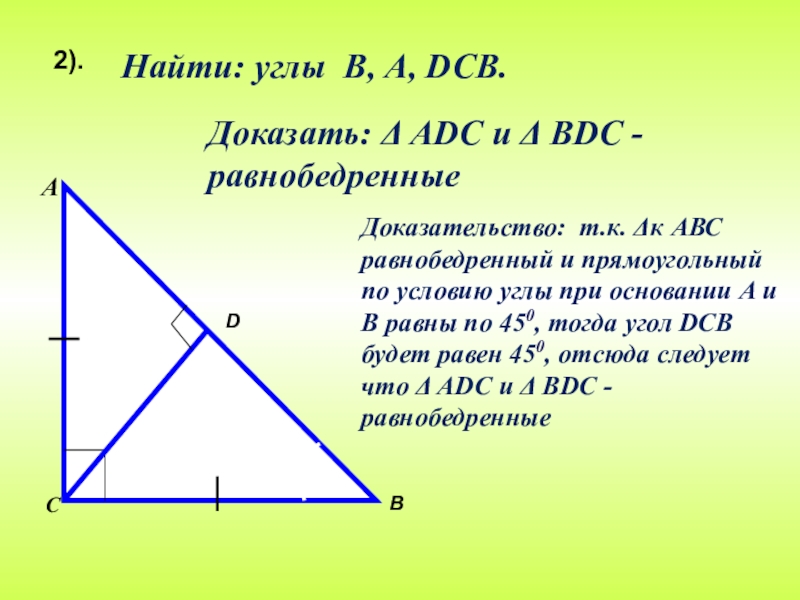
Найти: углы В, А, DСВ.
Доказать: Δ АDС и Δ ВDС -равнобедренные
2).
Доказательство:
т.к. Δк АВС равнобедренный и прямоугольный по условию углы при основании А и В равны по 450, тогда угол DСВ будет равен 450, отсюда следует что Δ АDС и Δ ВDС -равнобедренные
Слайд 28Задание 1: Тест
1. Прямоугольным называется треугольник, у которого
а) все углы прямые;
б) два угла прямые;
в) один прямой угол.
б) два угла прямые;
в) один прямой угол.
2. В прямоугольном треугольнике всегда
а) два угла острых и один прямой;
б) один острый угол, один прямой и один тупой угол;
в) все углы прямые.
Слайд 293. Стороны прямоугольного треугольника, образующие прямой угол, называются
а) сторонами треугольника;
б) катетами треугольника;
в) гипотенузами треугольника
б) катетами треугольника;
в) гипотенузами треугольника
4. Сумма острых углов прямоугольного треугольника равна
а) 180°; б) 100°; в) 90°.
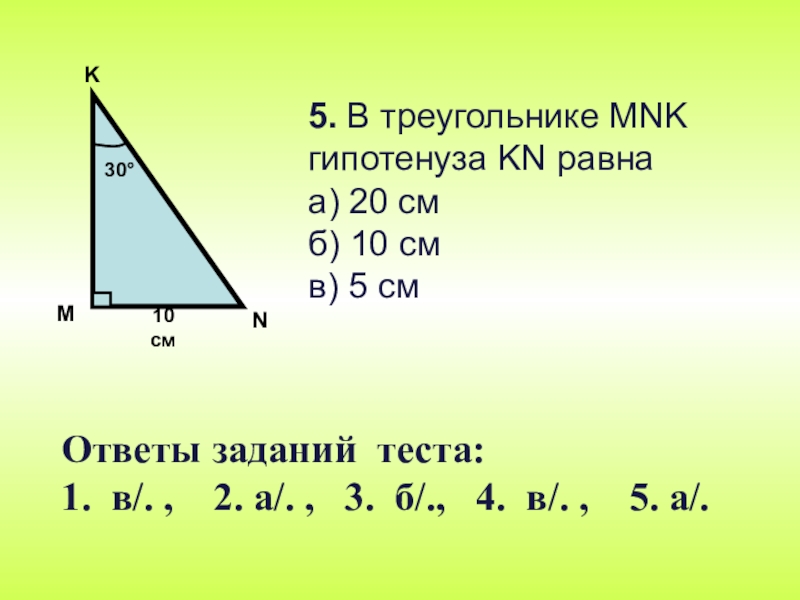
Слайд 305. В треугольнике MNK гипотенуза KN равна а) 20 см б) 10 см в)
5 см
Ответы заданий теста:
1. в/. , 2. а/. , 3. б/., 4. в/. , 5. а/.
Слайд 31Ответы задания №3
1, 3, 5, 6, 8, 11, 14, 16, 20
Ответы
задания №4
ВС= 5,
АВ = 16
АЕ = 14
углы В = С = 60
ВС= 5,
АВ = 16
АЕ = 14
углы В = С = 60
Слайд 32-Сумма двух острых углов прямоугольного
треугольника равна 90°
-Катет прямоугольного треугольника ,
лежащий против угла в 30°, равен половине гипотенузы.
-Если катет прямоугольного треугольника равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.
Подведем итог:
Слайд 33Я всё понял и могу доказать все свойства.
Я всё понял и
могу доказать некоторые свойства.
Для полного понимания мне необходимо повторить тему дома.
Я ничего не понял.
Для полного понимания мне необходимо повторить тему дома.
Я ничего не понял.
Слайд 34Итог самостоятельной работы:
Всего верно решенных задач _______
За 23-26 балл «5»,
За 19-22 балл «4»,
За 15-19 балл «3»
