- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме История тригонометрии 10 класс
Содержание
- 1. Презентация по геометрии по теме История тригонометрии 10 класс
- 2.
- 3. Цель данной работы – проследить путь
- 4. Что такое тригонометрия?
- 5. Начало истории тригонометрии как науки связано с
- 6. В Элладе гномон вводится учеником Фалеса Милетского
- 7. «Алмагест»
- 8. Известные труды по сферической тригонометрии были написаны
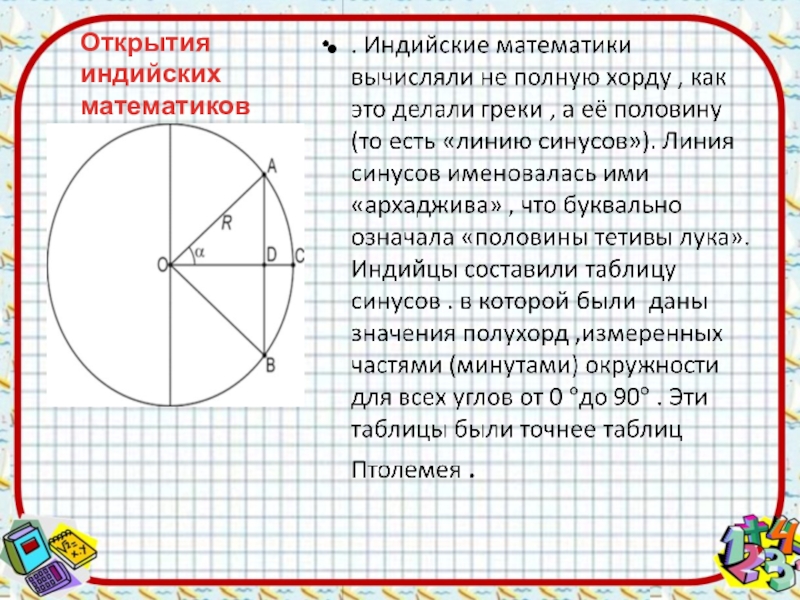
- 9. Открытия индийских математиков
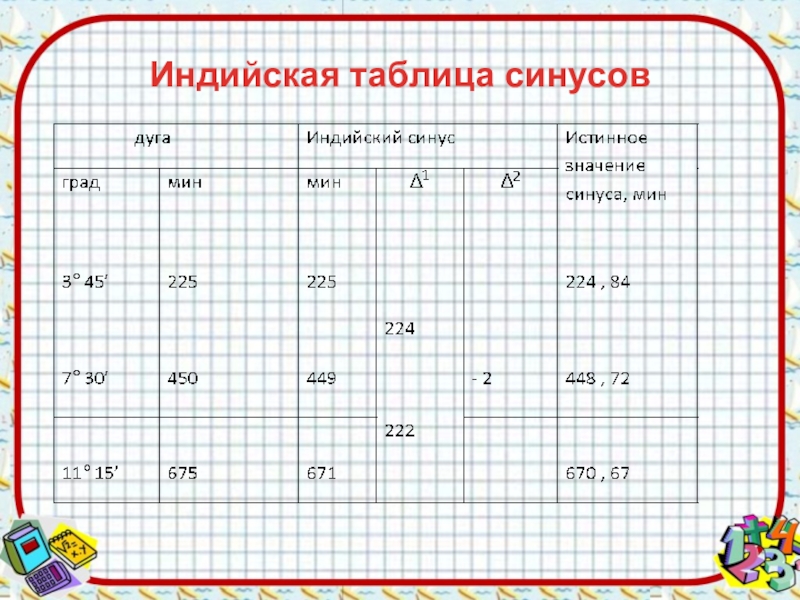
- 10. Индийская таблица синусов
- 11. Тригонометрия на Среднем и Ближнем ВостокеРаботы по
- 12. В 9-10 веках учёные стран ислама ал-Хабаш
- 13. Становление тригонометрии в ЕвропеАнглийский математик –Фома Брадвардии(1290-1349)
- 14. Теорема тангенсов (Региомонтана):.
- 15. Заслуги Леонарда Эйлера (1707—1783) Леонарда
- 16. Использование истории тригонометрии в школе
- 17. Слайд 17
Цель данной работы – проследить путь формирования тригонометрии как науки. Задачи:. Анализ имеющейся литературы по истории тригонометрии ;. Анализ школьного учебника А.Г.Мордковича . Объект исследования – тригонометрия , как научная дисциплина . Предмет исследования –
Слайд 1МБОУ «Благовещенская СОШ»
Оренбургская область Тюльганский район
История тригонометрии
выполнила :Климанова Ю.В.
Учитель математики
С.Благовещенка , 2018
Слайд 3 Цель данной работы – проследить путь формирования тригонометрии как науки.
Задачи:
. Анализ имеющейся литературы по истории тригонометрии ;
. Анализ школьного учебника А.Г.Мордковича .
Объект исследования – тригонометрия , как научная дисциплина .
Предмет исследования – использование историй тригонометрии в школе.
Метод исследования основан на историко –научном анализе соответствующей литературы.
. Анализ имеющейся литературы по истории тригонометрии ;
. Анализ школьного учебника А.Г.Мордковича .
Объект исследования – тригонометрия , как научная дисциплина .
Предмет исследования – использование историй тригонометрии в школе.
Метод исследования основан на историко –научном анализе соответствующей литературы.
Слайд 5
Начало истории тригонометрии как науки связано с деятельностью учёных Древней Греции
, которые унаследовали от египтян и вавилонян большой запас математических и астрономических фактов и вычислительных приёмов. Согласно легенде знаменитый древнегреческий философ и математик Фалес Милетский (VII-VI вв. до н.э.)познакомился в Египте с методом определения высоты предмета по известной длине его тени .
У своих восточных предшественников греки научились пользоваться гномоном- инструментом , служившим для наблюдения за движением Солнца.
У своих восточных предшественников греки научились пользоваться гномоном- инструментом , служившим для наблюдения за движением Солнца.
Слайд 6В Элладе гномон вводится учеником Фалеса Милетского –Анаксимандром (610-546 гг до
н.э. ).
Архимед(287-212 гг до н.э.) в трактате «Измерение круга» , а также в некоторых сочинениях , доказал теоремы , которые послужили основой для тригонометрических вычислений в круге.
Среди них особенно важна так называемая «лемма Архимеда»
Аристарх Самосский , автора сочинения «О размерах и расстояниях Солнца и Луны»
Архимед(287-212 гг до н.э.) в трактате «Измерение круга» , а также в некоторых сочинениях , доказал теоремы , которые послужили основой для тригонометрических вычислений в круге.
Среди них особенно важна так называемая «лемма Архимеда»
Аристарх Самосский , автора сочинения «О размерах и расстояниях Солнца и Луны»
Слайд 7 «Алмагест» Птолемея
Значительный вклад в развитие
тригонометрии внёс Клавдий Птолемей , производивший с 127 по 151 г. в Александрии свои наблюдения и умерший около 168 г., написал «Математическое собрание в 9 книгах» ,получившее позднее название «Альмагест».
Теорема Птолемея
sin (α + β) = sin α cos β + cos α sin β.
sin (α – β) = sin α cos β – cos α sin β.
Теорема Птолемея
sin (α + β) = sin α cos β + cos α sin β.
sin (α – β) = sin α cos β – cos α sin β.
Слайд 8
Известные труды по сферической тригонометрии были написаны в период 4 век
до н. э. -1 век н. э. такими выдающимися учёными древности , как Аутолик , Евклид , Теодосий , Менелай и др. Менелай Александрийский (100 н.э.)написал «Сферику» в трёх книгах ,Аутолик (ок .310 г.до н.э.)трактаты «О вращающейся сфере» и «О восходах и заходах»
.
.
Слайд 11Тригонометрия на Среднем и Ближнем Востоке
Работы по тригонометрии , как и
по математике вообще , арабские учёные начали с ознакомления с трудами своих предшественников. Около 773г. в Багдаде стала известна одна из индийских «сиддхант» , переведённая на арабский язык астрономом Абу Абдаллой Мухаммедом иби Ибрагимом ал-Фазари . В 9 веке были сделаны переводы «Алмагеста» Птолемея и «Сферики» Менелая , а также комментарии к ним . Три названных сочинения образовали фундамент ,на котором арабские математики стали успешно строить далее.
Слайд 12В 9-10 веках учёные стран ислама ал-Хабаш ,ал-Баттани(ок.850-929) ,Абул-Вафа(940-998) и другие
ввели новые тригонометрические величины: тангенс и котангенс, секанс и косеканс.
Ал-Хорезми(9 век) составил таблицы синусов и котангенсов и правила пользования этими таблицами.Большая заслуга в формировании тригонометрии как отдельной науки принадлежит учёному Насир ад-Дину Мухаммаду ат-Туси(1201–1274), написавшему «Трактат о полном четырёхугольнике». Работы учёных этого периода привели к выделению тригонометрии в самостоятельный раздел математики.
Ал-Хорезми(9 век) составил таблицы синусов и котангенсов и правила пользования этими таблицами.Большая заслуга в формировании тригонометрии как отдельной науки принадлежит учёному Насир ад-Дину Мухаммаду ат-Туси(1201–1274), написавшему «Трактат о полном четырёхугольнике». Работы учёных этого периода привели к выделению тригонометрии в самостоятельный раздел математики.
Слайд 13Становление тригонометрии в Европе
Английский математик –Фома Брадвардии(1290-1349) ввёл в употребление термины
«umbra recta» (прямая тень)и «umbra verca»(обращённая тень) , равносильные современным котангенсу и тангенсу.
Иоганн Мюллер(1436-1476) издал труд « Пять книг о треугольниках всех видов» ,сыгравший важную роль в развитии тригонометрии.
Франсуа Виет (1540- 1603) использовал тригонометрию для решения кубического уравнения. В некоторых его результатах устанавливалась связь между тригонометрией и алгеброй. Кроме того, он положил начало буквенным обозначениям в тригонометрии.
Иоганн Мюллер(1436-1476) издал труд « Пять книг о треугольниках всех видов» ,сыгравший важную роль в развитии тригонометрии.
Франсуа Виет (1540- 1603) использовал тригонометрию для решения кубического уравнения. В некоторых его результатах устанавливалась связь между тригонометрией и алгеброй. Кроме того, он положил начало буквенным обозначениям в тригонометрии.
Слайд 15Заслуги Леонарда Эйлера (1707—1783)
Леонарда Эйлер впервые доступно изложил
вопрос о знаках тригонометрических функций в каждом квадранте , установил формулы приведения , подробно исследовав области определения этих функций и обозначив их символами: sin х, соs x, tang x, соt х .
Эйлер усовершенствовал как символику ,так и содержание тригонометрии.
Эйлер усовершенствовал как символику ,так и содержание тригонометрии.