- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Перпендикуляр и наклонная (1 курс СПО)
Содержание
- 1. Презентация по геометрии Перпендикуляр и наклонная (1 курс СПО)
- 2. Расстояние от точки до плоскостиAHMαAH - перпендикулярH
- 3. ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХмНАаαПрямая, проведенная в плоскости
- 4. Угол между наклонной и плоскостьюУглом между прямой
- 5. Концы отрезка отстоят от плоскости α на
- 6. Расстояние от точки М до каждой из
- 7. 154 Прямая BD перпендикулярна к плоскости треугольника
Расстояние от точки до плоскостиAHMαAH - перпендикулярH - основание перпендикуляраAM - наклоннаяMH - проекция наклоннойПерпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости. (AH < AM)AH –
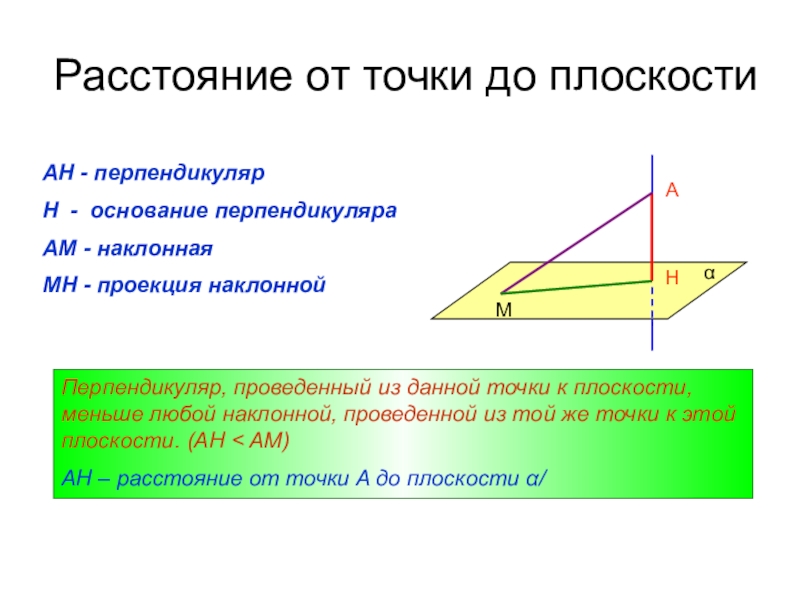
Слайд 2Расстояние от точки до плоскости
A
H
M
α
AH - перпендикуляр
H - основание перпендикуляра
AM -
наклонная
MH - проекция наклонной
MH - проекция наклонной
Перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости. (AH < AM)
AH – расстояние от точки A до плоскости α/
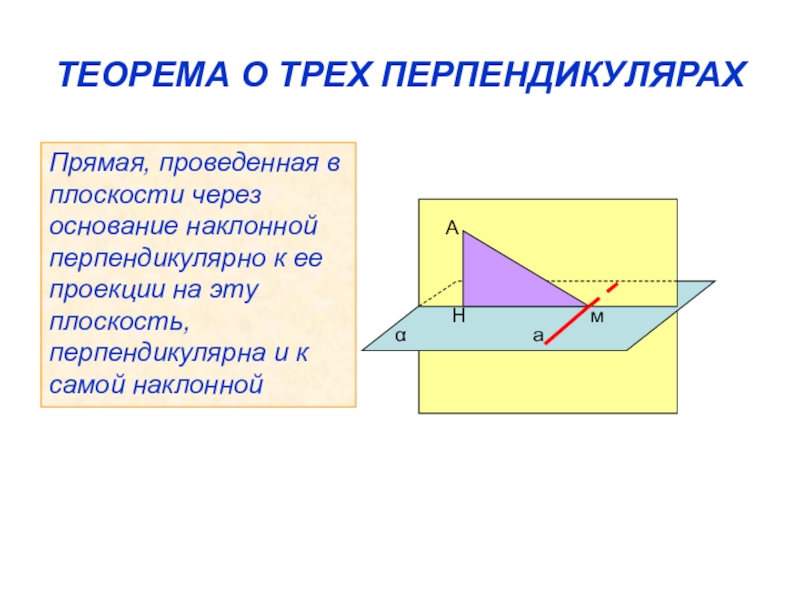
Слайд 3ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
м
Н
А
а
α
Прямая, проведенная в плоскости через основание наклонной перпендикулярно
к ее проекции на эту плоскость, перпендикулярна и к самой наклонной
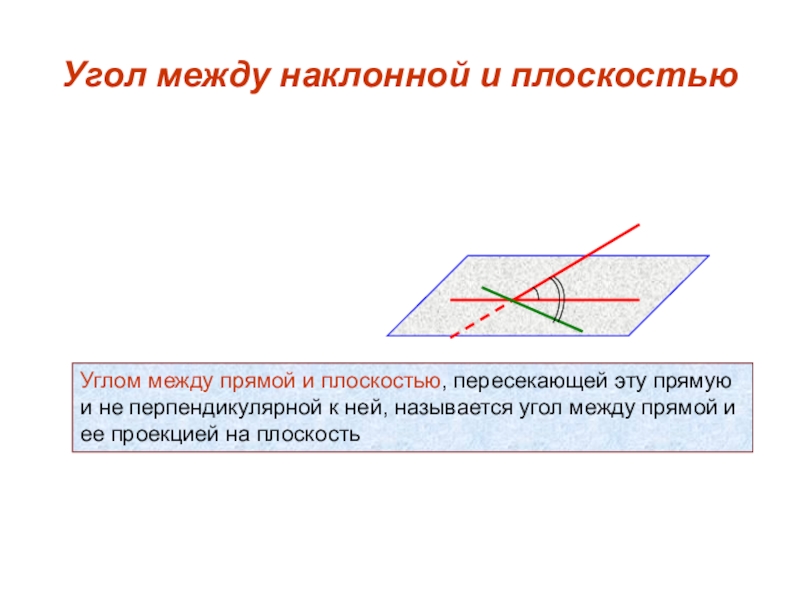
Слайд 4Угол между наклонной и плоскостью
Углом между прямой и плоскостью, пересекающей эту
прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость
Слайд 5Концы отрезка отстоят от плоскости α на расстояниях 1м и 4м.
Найти расстояние от середины отрезка до плоскости α.
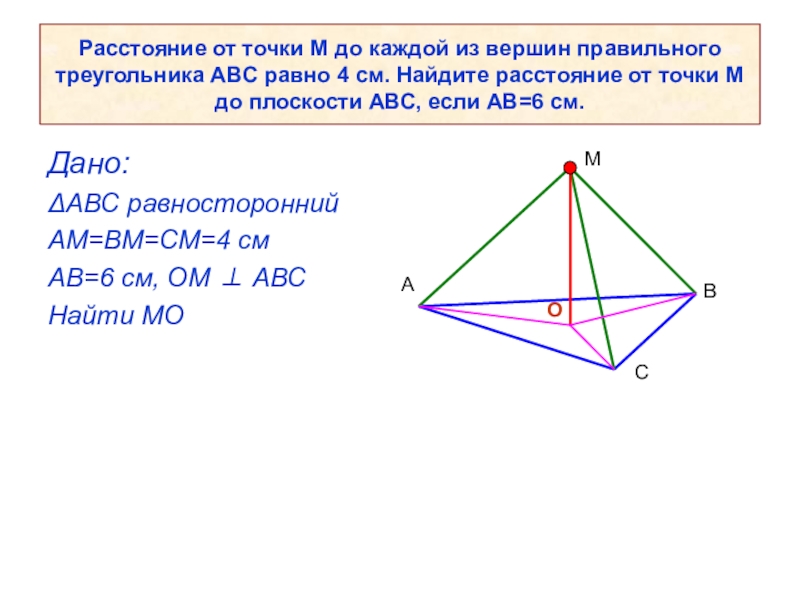
Слайд 6Расстояние от точки М до каждой из вершин правильного треугольника АВС
равно 4 см. Найдите расстояние от точки М до плоскости АВС, если АВ=6 см.
Дано:
ΔАВС равносторонний
АМ=ВМ=СМ=4 см
АВ=6 см, ОМ АВС
Найти МО
А
М
В
С
О
Слайд 7154 Прямая BD перпендикулярна к плоскости треугольника АВС. Известно, что BD=9см,
AC=10 см, BC=BA=13 см. Найдите: а) расстояние от точки D до прямой АС; б) площадь треугольника АСD
Дано:
BD ABC, BD=9 см, АС=10 см,
ВС=ВА=13 см
Найти:
а) расстояние от D до АС
в) S ΔACD
D
B
C
A
N
Решение
