- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Параллелограмм
Содержание
- 1. Презентация по геометрии Параллелограмм
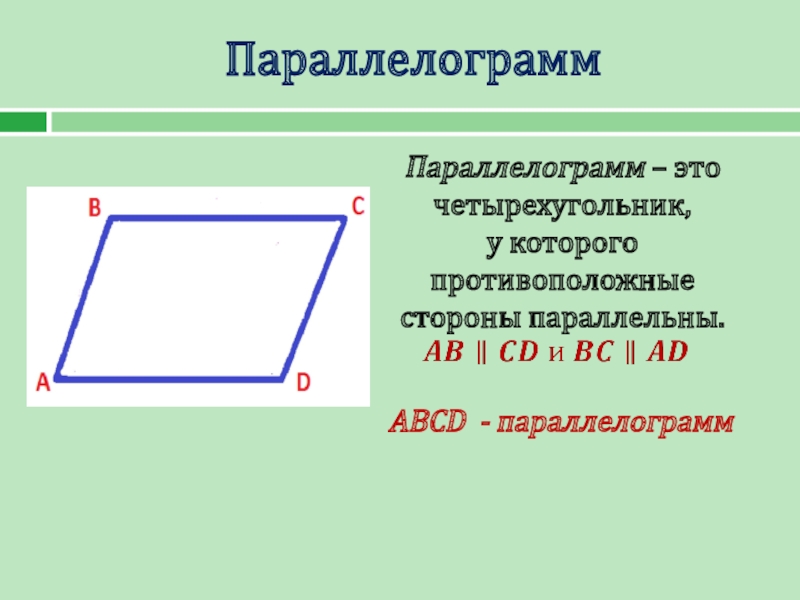
- 2. ПараллелограммABCD - параллелограмм
- 3. АВСD1234Какими свойствами обладает параллелограмм?
- 4. Свойство 1. В параллелограмме противоположные
- 5. Свойство 2. Диагонали параллелограмма точкой
- 6. Решите задачу1MNPK7 см 4 см Найдите периметр
- 7. Решите задачу. В параллелограмме ABCD:
- 8. В параллелограмме ABCD проведена диагональ AC. ∠BCA
- 9. Найдите стороны параллелограмма, если две его стороны
Слайд 4
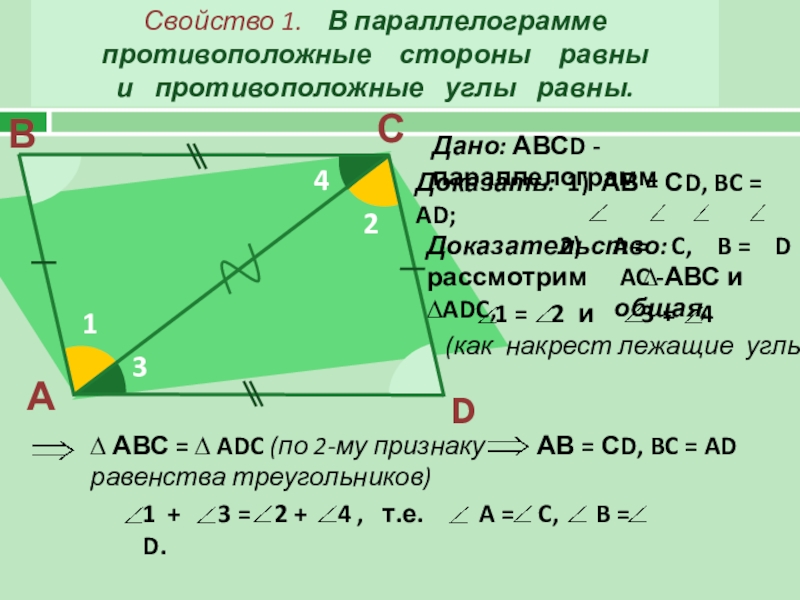
Свойство 1. В параллелограмме противоположные стороны равны
и
А
В
С
D
Дано: АВСD - параллелограмм
Доказательство: рассмотрим ∆ АВС и ∆ADC,
AC - общая,
1
2
3
4
АВ = СD, BC = AD
Слайд 5Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.
В
А
С
D
1
3
4
Дано: АВСD
Доказать: ВО = ОD, АО = ОС
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
Следовательно: АО = ОС, ВО = ОD
O
АВ = СD (противоположные стороны параллелограмма,
2
Слайд 6
Решите задачу
1
M
N
P
K
7 см
4 см
Найдите периметр параллелограмма MNPK
2
70°
Найдите все углы
Решение
7 см
4 см
Р = (7 + 4) · 2 = 22 (см)
70°
110°
110°
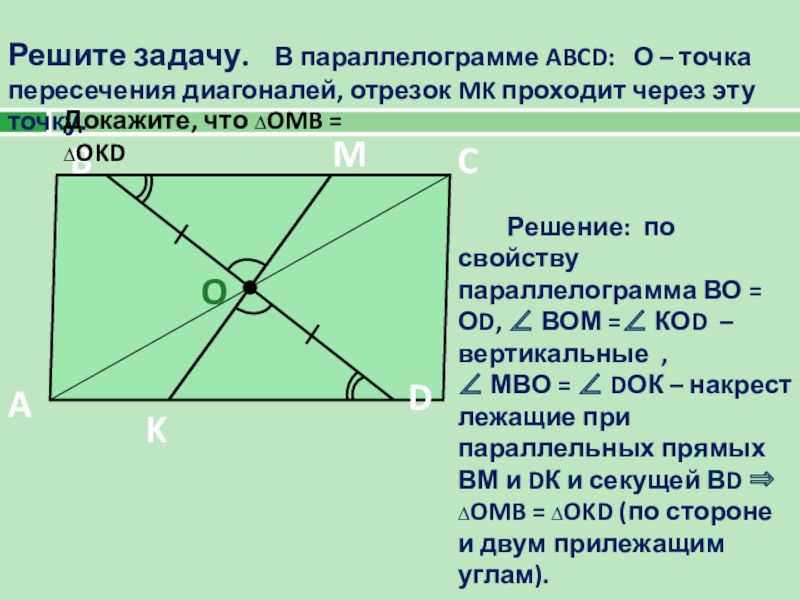
Слайд 7Решите задачу. В параллелограмме ABCD: О – точка пересечения
A
B
C
D
O
K
M
Решение: по свойству параллелограмма ВО = ОD, ∠ ВОМ =∠ КОD – вертикальные ,
∠ МВО = ∠ DОК – накрест лежащие при параллельных прямых ВМ и DК и секущей ВD ⇒ ∆OMB = ∆OKD (по стороне и двум прилежащим углам).
Докажите, что ∆OMB = ∆OKD
Слайд 8В параллелограмме ABCD проведена диагональ AC. ∠BCA = 30°, ∠BAC =
Найдите все углы параллелограмма.
Решение:
∠B = ∠D = 110°
(по свойству противоположных углов),
∠A+∠B=180°, ⇒
∠A=180°-110°=70°, ∠C=∠A=70°
(по свойству противоположных
углов параллелограмма)
Ответ: ∠C=∠A=70°, ∠B = ∠D = 110°
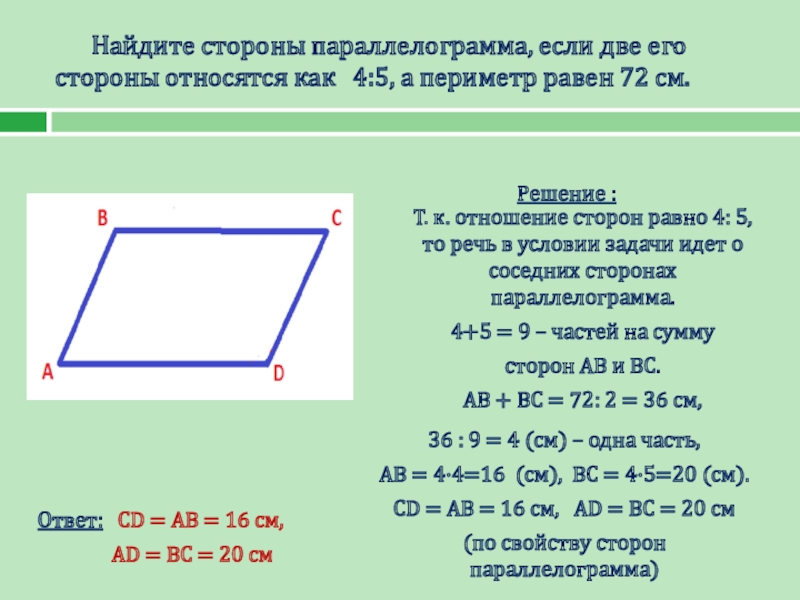
Слайд 9 Найдите стороны параллелограмма, если две его стороны относятся как 4:5,
Решение :
Т. к. отношение сторон равно 4: 5, то речь в условии задачи идет о соседних сторонах параллелограмма.
4+5 = 9 – частей на сумму
сторон AB и BC.
AB + BC = 72: 2 = 36 см,
36 : 9 = 4 (см) – одна часть,
AB = 4·4=16 (см), BC = 4·5=20 (см).
CD = AB = 16 см, AD = BC = 20 см
(по свойству сторон параллелограмма)
Ответ: CD = AB = 16 см,
AD = BC = 20 см