- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Параллельные прямые. Свойство параллельных прямых
Содержание
- 1. Презентация по геометрии Параллельные прямые. Свойство параллельных прямых
- 2. Задачи на повторениеПо данным рисунка определите, есть
- 3. Задача 1 Прямая d пересекает прямую b.
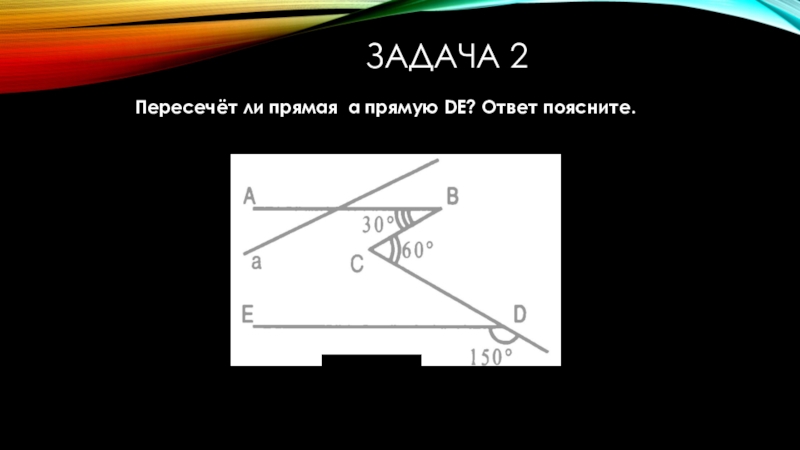
- 4. Задача 2 Пересечёт ли прямая а прямую
- 5. Слайд 5
- 6. Тест самопроверки
- 7. 3. Указать правильный ответ на вопрос:Если через
- 8. Слайд 8
- 9. 5. Указать правильный ответ на вопрос:Если через
- 10. Ответы к тесту1) Вычеркнуть: очевидно, принятые, объяснений, обоснований;2) а;3) а,б;4) б,в,е,ж;5) б
- 11. Решить задачу Доказать: АВ II CD;б) Дано
- 12. Свойства параллельных прямыхРешение этих задач приводит
- 13. Слайд 13
- 14. то, что
- 15. Слайд 15
- 16. ТеоремаЕсли две параллельные прямые пересечены секущей, то
- 17. Слайд 17
- 18. Слайд 18
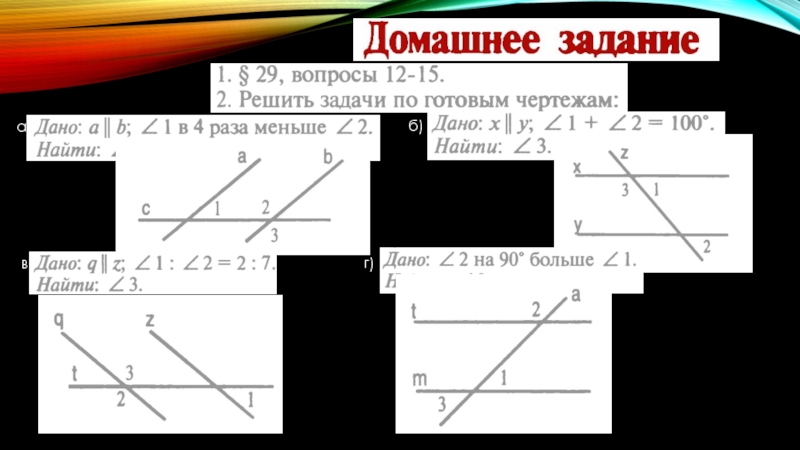
- 19. а) б) в) г)
Задачи на повторениеПо данным рисунка определите, есть ли там параллельные прямые. Ответ обоснуйте.L1 II L4L2 II L5
Слайд 2Задачи на повторение
По данным рисунка определите, есть ли там параллельные прямые.
Ответ обоснуйте.
L1 II L4
L2 II L5
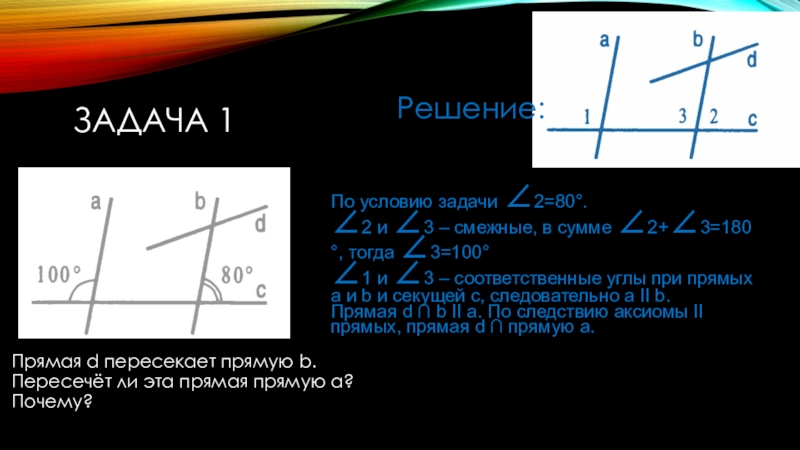
Слайд 3Задача 1
Прямая d пересекает прямую b. Пересечёт ли эта прямая
прямую а? Почему?
Решение:
По условию задачи 2=80°.
2 и 3 – смежные, в сумме 2+3=180 °, тогда 3=100°
1 и 3 – соответственные углы при прямых а и b и секущей с, следовательно а II b.
Прямая d ∩ b II a. По следствию аксиомы II прямых, прямая d ∩ прямую a.
Слайд 6Тест самопроверки
1. Выпишите лишние слова в скобках:
Аксиома – это (очевидные, принятые, исходные) положения геометрии, не требующие (объяснений, доказательств, обоснований).
2. Выбрать окончание формулировки аксиомы параллельных прямых: Через точку, не лежащую на данной прямой, проходит:
а) только одна прямая параллельная данной;
б) всегда проходит прямая параллельная данной;
в) только одна прямая, не пресекающаяся с данной.
Аксиома – это (очевидные, принятые, исходные) положения геометрии, не требующие (объяснений, доказательств, обоснований).
2. Выбрать окончание формулировки аксиомы параллельных прямых: Через точку, не лежащую на данной прямой, проходит:
а) только одна прямая параллельная данной;
б) всегда проходит прямая параллельная данной;
в) только одна прямая, не пресекающаяся с данной.
Слайд 73. Указать правильный ответ на вопрос:
Если через точку, лежащую вне прямой,
проведено несколько прямых, то сколько из них пересекаются с исходной прямой?
а) Неизвестно, так как не сказано, сколько прямых проведено через точку;
б) Все, кроме параллельной прямой;
в) Все, которые имеют на рисунке точку пересечения с исходной прямой.
а) Неизвестно, так как не сказано, сколько прямых проведено через точку;
б) Все, кроме параллельной прямой;
в) Все, которые имеют на рисунке точку пересечения с исходной прямой.
Слайд 8
4. Указать следствия аксиомы параллельных прямых:
а) Если отрезок или луч, пересекает одну из параллельных прямых, то он и пересекает другую;
б) Если две прямые параллельны третьей прямой, то они параллельны друг другу;
в) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
г) Если три прямые параллельны, то любые две из них параллельны друг другу;
д) Если две прямые не параллельные третьей прямой, то они не параллельны между собой;
е) Если прямая пересекает одну из двух параллельных прямых, то она не может и пересекать прямую;
ж) Если две прямые параллельны третьей прямой, то они не могут быть не параллельны между собой.
а) Если отрезок или луч, пересекает одну из параллельных прямых, то он и пересекает другую;
б) Если две прямые параллельны третьей прямой, то они параллельны друг другу;
в) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
г) Если три прямые параллельны, то любые две из них параллельны друг другу;
д) Если две прямые не параллельные третьей прямой, то они не параллельны между собой;
е) Если прямая пересекает одну из двух параллельных прямых, то она не может и пересекать прямую;
ж) Если две прямые параллельны третьей прямой, то они не могут быть не параллельны между собой.
Слайд 95. Указать правильный ответ на вопрос:
Если через точку, лежащую вне прямой,
проведено
несколько прямых, то сколько из них пересекаются с
исходной прямой?
а) Неизвестно, так как не сказано, сколько прямых проведено через точку.
б) Все кроме параллельной прямой.
в) Все, которые имеют на рисунке точку пересечения с исходной прямой
несколько прямых, то сколько из них пересекаются с
исходной прямой?
а) Неизвестно, так как не сказано, сколько прямых проведено через точку.
б) Все кроме параллельной прямой.
в) Все, которые имеют на рисунке точку пересечения с исходной прямой
Слайд 10Ответы к тесту
1) Вычеркнуть: очевидно, принятые, объяснений, обоснований;
2) а;
3) а,б;
4) б,в,е,ж;
5)
б
Слайд 11Решить задачу
Доказать: АВ II CD;
б) Дано АВ II CD. Найти
ЕКС.
обратите внимание!!!
В первой задаче АВ II CD по 1 признаку II прямых, вторая задача является обратной первой, мы не знаем равны ли накрест лежащие углы, если прямые II.
Сформулируйте тему урока.
обратите внимание!!!
В первой задаче АВ II CD по 1 признаку II прямых, вторая задача является обратной первой, мы не знаем равны ли накрест лежащие углы, если прямые II.
Сформулируйте тему урока.
Слайд 12Свойства
параллельных прямых
Решение этих задач приводит к выводу:
Если две параллельные прямые
пересечены третьей, то накрест лежащие углы равны.
Это утверждение называется свойство накрест лежащих углов.
Это утверждение называется свойство накрест лежащих углов.
Слайд 16Теорема
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
Дано: аǁb, MN- секущая
<1, <2 - - накрест лежащие углы
Доказать: <1=<2
Доказательство:
Пусть <1 ≠ <2. Отложим от луча MN угол PMN = <2, так, чтобы
Теорема доказана.