- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Основные задачи на построение.Урок №2. (7 класс)
Содержание
- 1. Презентация по геометрии Основные задачи на построение.Урок №2. (7 класс)
- 2. Цели урока:Рассмотреть основные (простейшие) задачи на построение:отложить
- 3. 1. Что называется биссектрисой угла?
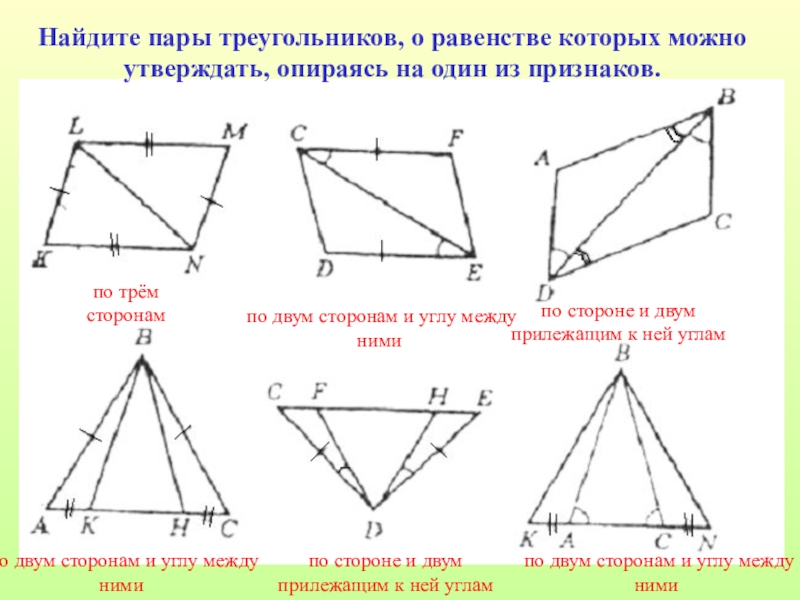
- 4. Найдите пары треугольников, о равенстве которых можно
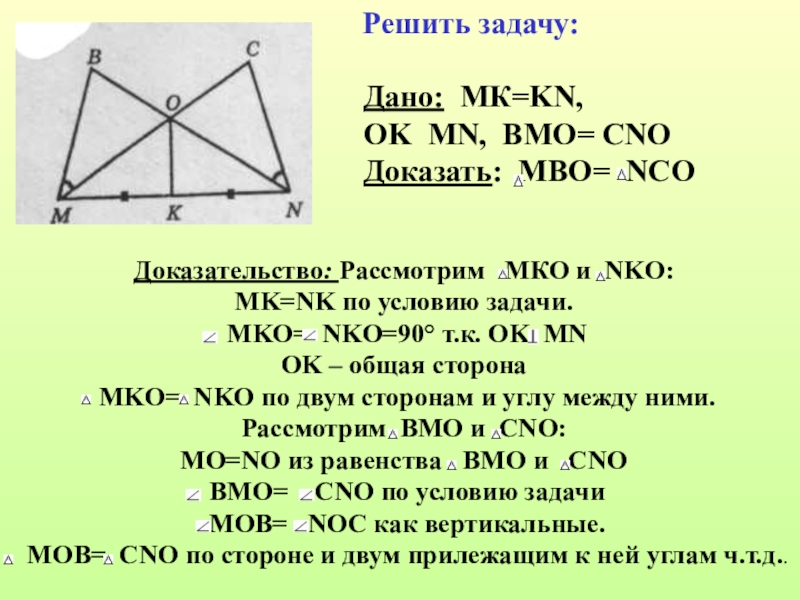
- 5. Решить задачу: Дано: МК=KN, OK MN, ВМО= CNO Доказать: МВО= NCO
- 6. Какое название происходит от двух латинских слов
- 7. Биссектриса лат. слова bis –
- 8. способы построения биссектрисы: Перегиб модели угла С помощью транспортира С помощью циркуля и линейки
- 9. Постановка проблемы урока Прочитайте задачи:
- 10. А теперь попробуйте выполнить эти же построения с помощью циркуля и линейки без делений.
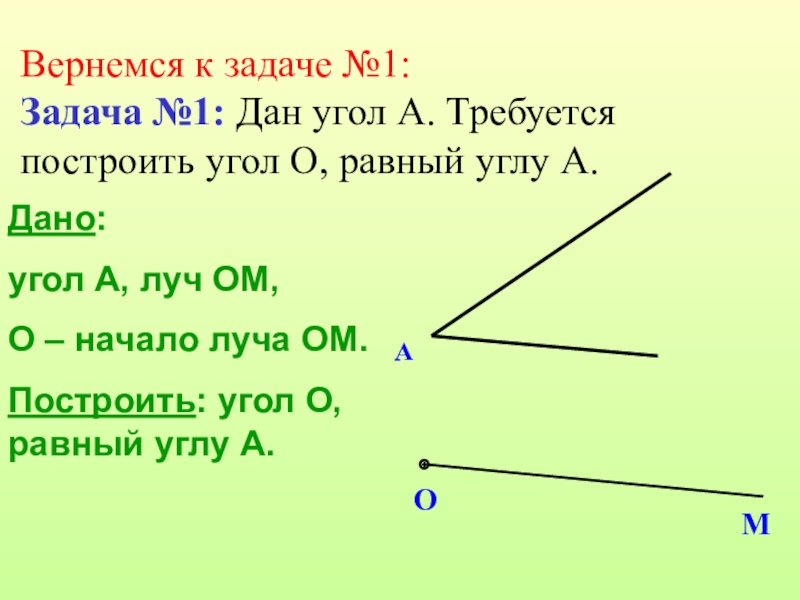
- 11. Дано: угол А, луч ОМ,О – начало
- 12. АВСОDEМШаг 1.Построим окружность произвольного радиуса с центром
- 13. Докажем,что А = ОДано: угол А.Построили угол О.
- 14. Дано: угол АПостроить: биссектрису угла А Вернемся
- 15. Шаг 3. Проведём луч АB, который и
- 16. Докажем, что луч АВ – биссектриса
- 17. Спасибо за урок
Слайд 1учитель математики МБОУ Фёдоровская СОШ
Архипова Ирина Александровна
Геометрия
7 класс
Основные задачи
Слайд 2Цели урока:
Рассмотреть основные (простейшие) задачи на построение:
отложить от данного луча угол,
построить биссектрису данного угла.
Слайд 31. Что называется биссектрисой угла?
3. Какие углы называются равными?
4. Каким свойством обладает медиана равнобедренного треугольника, проведенная к основанию?
Устная работа:
2. Что называется медианой?
Слайд 4Найдите пары треугольников, о равенстве которых можно утверждать, опираясь на один
по двум сторонам и углу между ними
по стороне и двум прилежащим к ней углам
по трём сторонам
по двум сторонам и углу между ними
по стороне и двум прилежащим к ней углам
по двум сторонам и углу между ними
Слайд 6Какое название происходит
от двух латинских слов
«дважды» и «секу»,
буквально
на две части».
О чем идет речь?
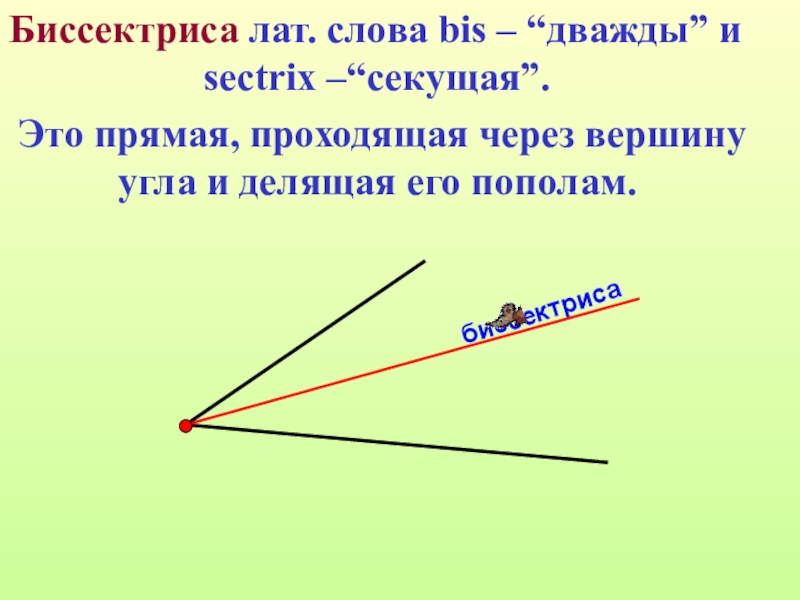
Слайд 7 Биссектриса лат. слова bis – “дважды” и sectrix –“секущая”.
Это прямая, проходящая через вершину угла и делящая его пополам.
биссектриса
Слайд 8способы построения
биссектрисы:
Перегиб модели угла
С помощью транспортира
С помощью
Слайд 9Постановка проблемы урока Прочитайте задачи: Задача №1: Дан угол А. Требуется построить
Слайд 11
Дано:
угол А, луч ОМ,
О – начало луча ОМ.
Построить: угол О,
А
О
М
Вернемся к задаче №1:
Задача №1: Дан угол А. Требуется построить угол О, равный углу А.
Слайд 12А
В
С
О
D
E
М
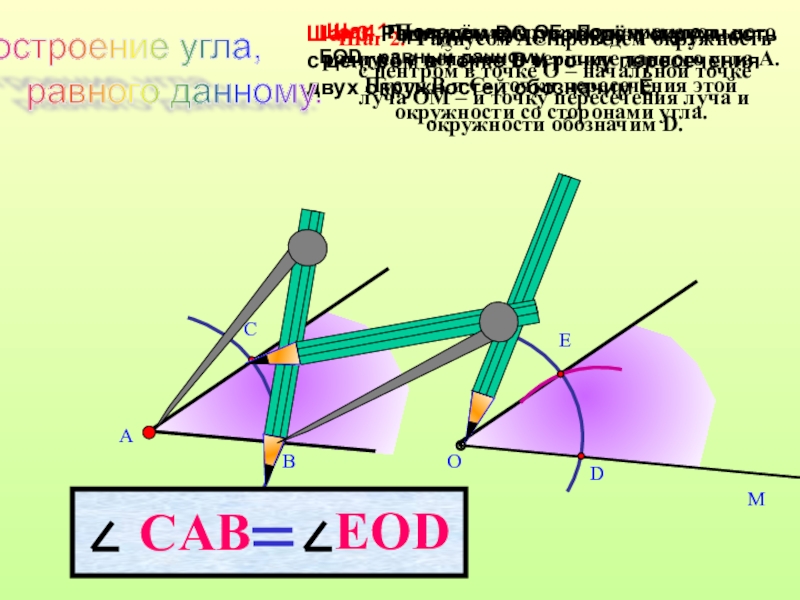
Шаг 1.Построим окружность произвольного радиуса с центром в вершине данного угла
Пусть B и C- точки пересечения этой окружности со сторонами угла.
Шаг 2. Радиусом АС проведём окружность с центром в точке О – начальной точке луча ОМ – и точку пересечения луча и окружности обозначим D.
Шаг 3. Радиусом ВС проведём окружность с центром в точке D и точку пересечения двух окружностей обозначим Е.
Шаг 4. Проведём луч ОЕ.. Получим угол ЕОD,, равный данному.
Построение угла,
равного данному.
Слайд 14
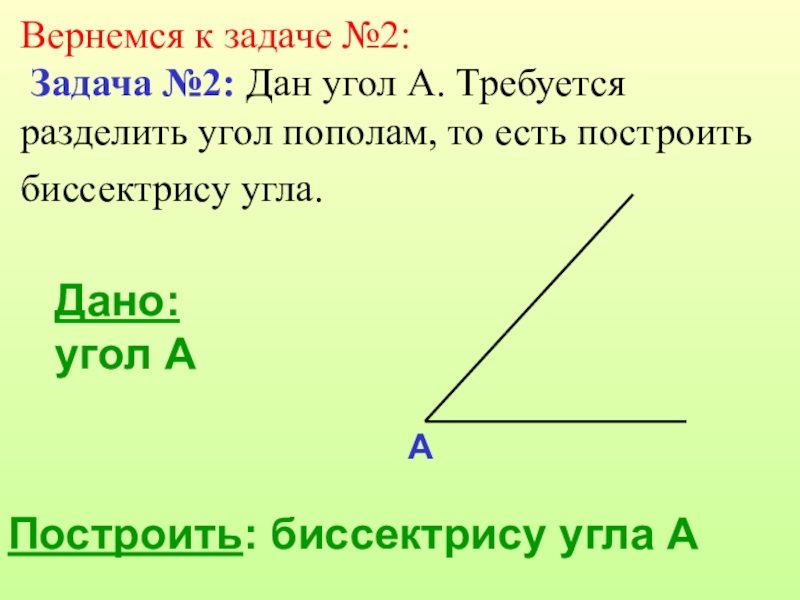
Дано: угол А
Построить: биссектрису угла А
Вернемся к задаче №2:
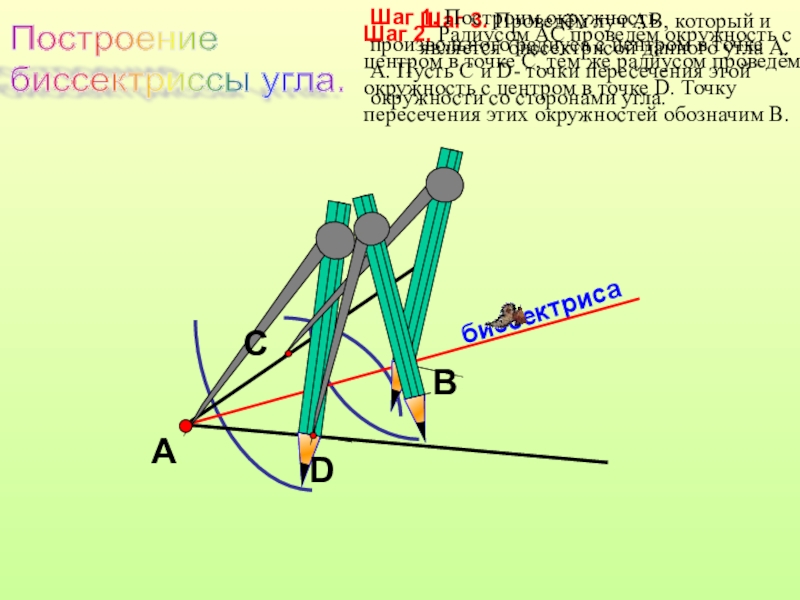
Слайд 15Шаг 3. Проведём луч АB, который и является биссектрисой данного угла
Шаг 1. Построим окружность произвольного радиуса с центром в точке А. Пусть С и D- точки пересечения этой окружности со сторонами угла.
Шаг 2. Радиусом АС проведём окружность с центром в точке C, тем же радиусом проведём окружность с центром в точке D. Точку пересечения этих окружностей обозначим B.
биссектриса
А
D
C
B
Построение
биссектриссы угла.
Слайд 16
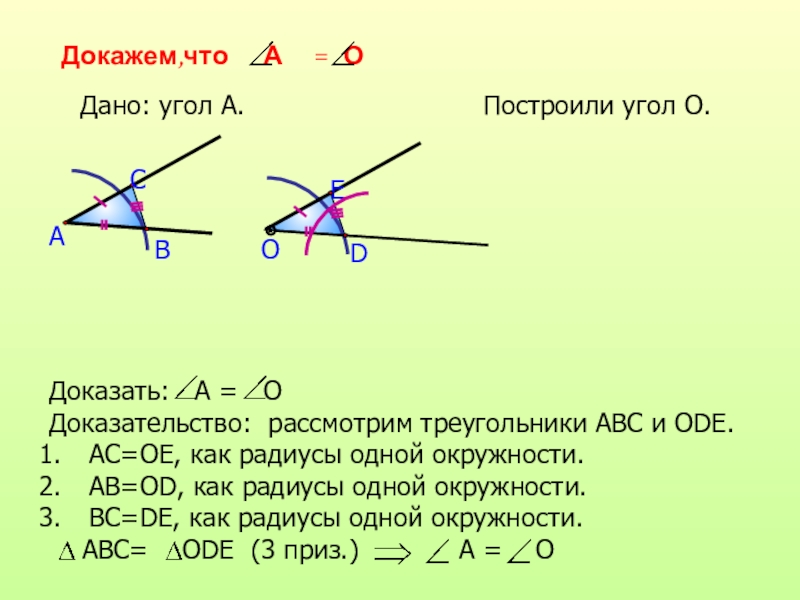
Докажем, что луч АВ – биссектриса А
Доказательство:
Выполним дополнительное
Докажем равенство
треугольников ∆ АСВ и ∆ АDB.
А
В
С
D
АС=АD, как радиусы одной окружности.
СВ=DB, как радиусы одной окружности.
АВ – общая сторона.
∆АСВ = ∆ АDВ, по III признаку
равенства треугольников
Луч АВ – биссектриса