6»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Описанные и вписанные шары ( 11 класс)
Содержание
- 1. Презентация по геометрии Описанные и вписанные шары ( 11 класс)
- 2. Описанные шарыШар называется описанным около многогранника,
- 3. Многогранники, вписанные в шарЦентр описанного около многогранника
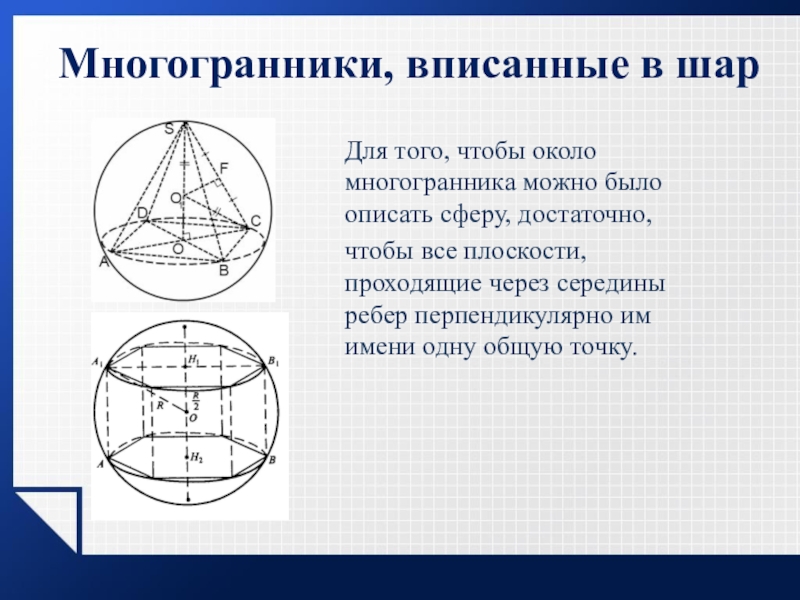
- 4. Для того, чтобы около многогранника можно было
- 5. Вписанная пирамидаДля того, чтобы около пирамиды можно
- 6. Вписанная призмаДля того, чтобы около призмы можно
- 7. Вписанный конусДля того, чтобы около конуса можно
- 8. Вписанный цилиндрДля того, чтобы около цилиндра можно
- 9. Вписанный конус или шар, описанный около конусаАВ
- 10. Задача 1Около конуса описан шар. Найти радиус
- 11. Задача 2Найти радиус описанной около основания окружности
- 12. Задача 3 Найти радиус шара, описанного около
- 13. Задача 4В правильной треугольной пирамиде сторона основания
- 14. Ответ: 2 см
- 15.
- 16.
- 17.
- 18. Вписанные шарыШар называется вписанным в многогранник, а
- 19. Вписанные шарыШар называется вписанным в конус, усеченный
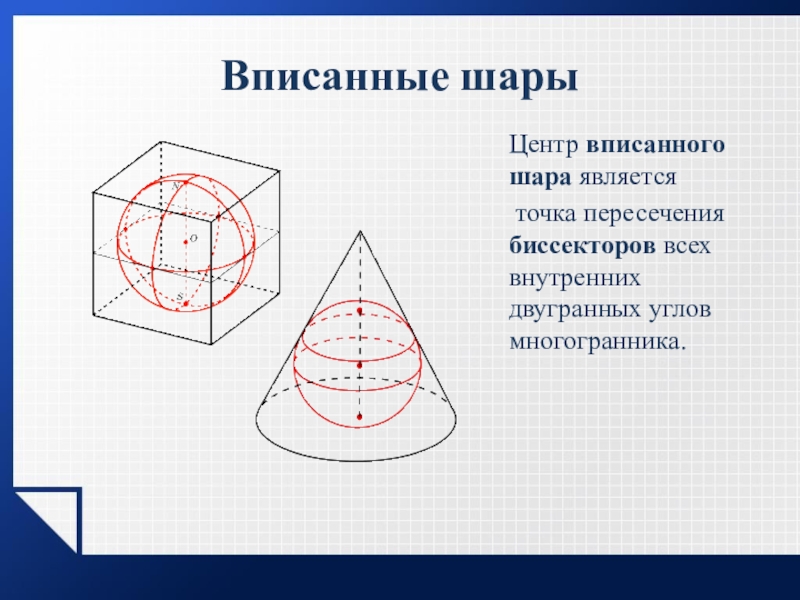
- 20. Вписанные шарыЦентр вписанного шара является точка пересечения биссекторов всех внутренних двугранных углов многогранника.
- 21. Центр вписанной сферы является точка пересечения биссекторов всех внутренних двугранных углов многогранника.
- 22. Шар, вписанный в призмуДля того, чтобы в
- 23. Шар, вписанный в призмуШар можно вписать в
- 24. Шар, вписанный в конусЦентр вписанного в конус
- 25. Шар, вписанный в пирамидуВ треугольную и любую
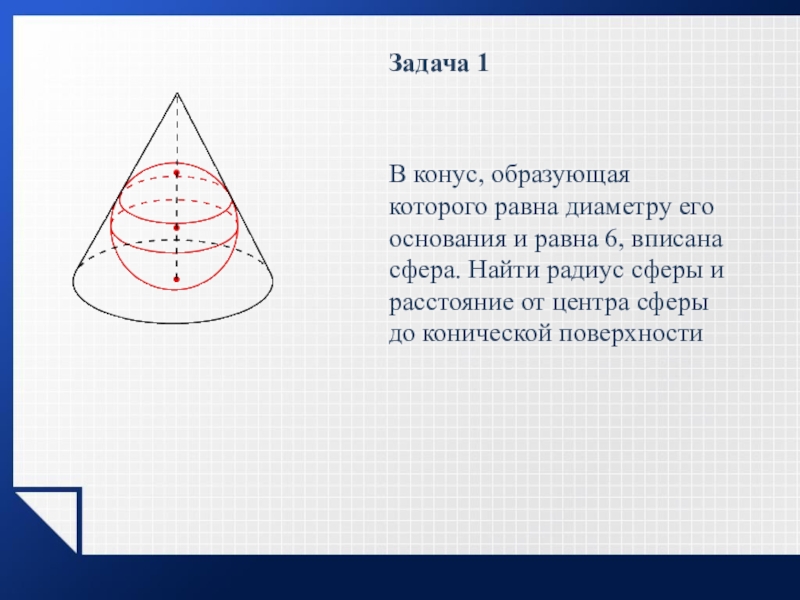
- 26. Задача 1 В конус, образующая которого равна
- 27. Задача 2 Найти радиус шара, вписанного в
Описанные шарыШар называется описанным около многогранника, а многогранник вписанным в этот шар, если все вершины многогранника лежат на поверхности шара. Чтобы около многогранника можно было описать сферу, необходимо и достаточно, чтобы каждая его грань была
Слайд 2 Описанные шары
Шар называется описанным около многогранника, а многогранник вписанным в
этот шар, если все вершины многогранника лежат на поверхности шара.
Чтобы около многогранника можно было описать сферу, необходимо и достаточно,
чтобы каждая его грань была многогранником, около которого можно было описать окружность.
Слайд 3Многогранники, вписанные в шар
Центр описанного около многогранника шара есть точка, равноудаленная
от всех его вершин. Геометрическое место точек, равноудаленных от всех вершин какой-либо грани, есть прямая, перпендикулярная к плоскости грани и проходящая через центр описанной около нее окружности.
Геометрическое место точек, равноудаленных от концов какой-либо ребра, есть плоскость, перпендикулярная ребру и проходящая через его середину. Значит, центр шара принадлежит одновременно двум указанным геометрическим местам
Геометрическое место точек, равноудаленных от концов какой-либо ребра, есть плоскость, перпендикулярная ребру и проходящая через его середину. Значит, центр шара принадлежит одновременно двум указанным геометрическим местам
Слайд 4Для того, чтобы около многогранника можно было описать сферу, достаточно,
чтобы
все плоскости, проходящие через середины ребер перпендикулярно им имени одну общую точку.
Многогранники, вписанные в шар
Слайд 5Вписанная пирамида
Для того, чтобы около пирамиды можно было описать сферу, необходимо
и достаточно,
чтобы около основания пирамиды можно было описать окружность.
чтобы около основания пирамиды можно было описать окружность.
Слайд 6Вписанная призма
Для того, чтобы около призмы можно было описать сферу, необходимо
и достаточно,
чтобы призма была прямой и около основания призмы можно было описать окружность.
чтобы призма была прямой и около основания призмы можно было описать окружность.
Слайд 7Вписанный конус
Для того, чтобы около конуса можно было описать сферу, необходимо
и достаточно,
( без условий)
Шар называется описанным около конуса, если поверхность шара проходит через вершину конуса, а окружность основания конуса лежит на поверхности шара.
( без условий)
Шар называется описанным около конуса, если поверхность шара проходит через вершину конуса, а окружность основания конуса лежит на поверхности шара.
Слайд 8Вписанный цилиндр
Для того, чтобы около цилиндра можно было описать сферу, необходимо
и достаточно,
( без условий)
Шар называется описанным около цилиндра , если окружности его оснований лежат на поверхности шара.
( без условий)
Шар называется описанным около цилиндра , если окружности его оснований лежат на поверхности шара.
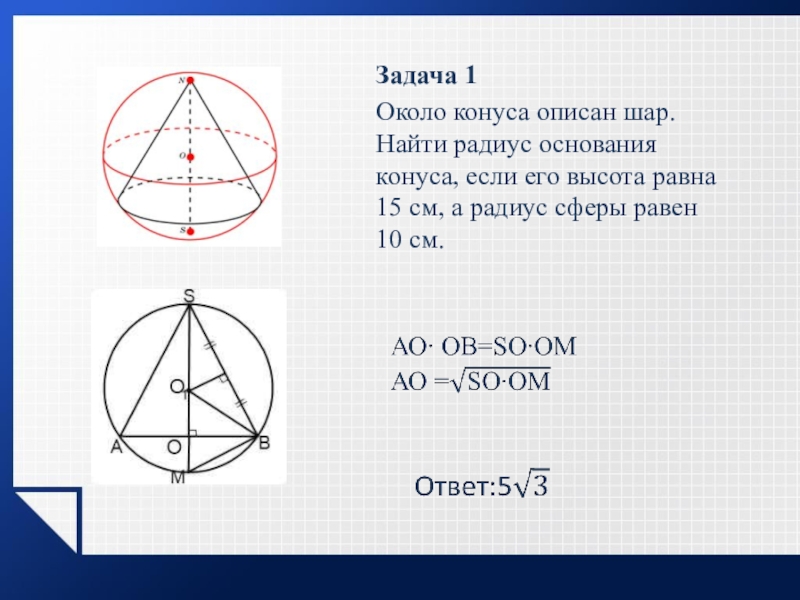
Слайд 10Задача 1
Около конуса описан шар. Найти радиус основания конуса, если его
высота равна 15 см, а радиус сферы равен 10 см.
Слайд 11Задача 2
Найти радиус описанной около основания окружности в треугольной пирамиде, если
высота пирамиды 20 см, а радиус описанной сферы, равен 15 см.
М
К
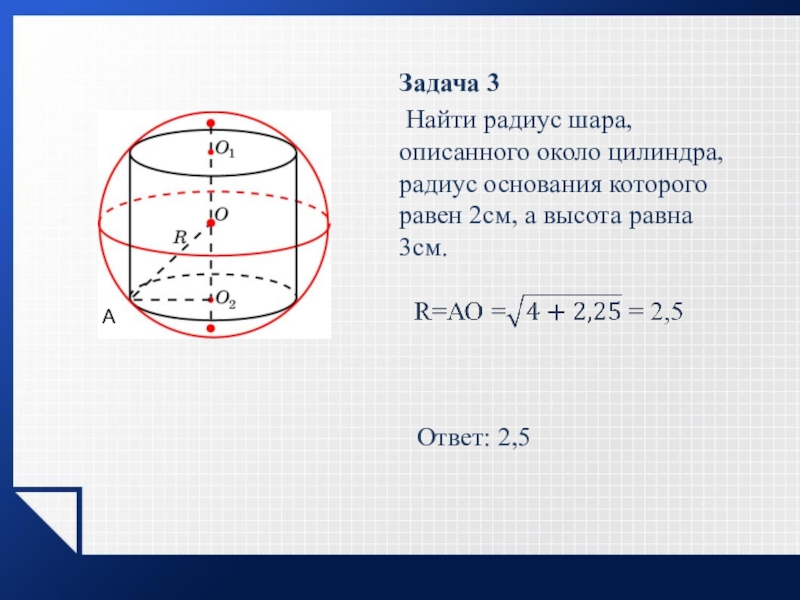
Слайд 12Задача 3
Найти радиус шара, описанного около цилиндра, радиус основания которого
равен 2см, а высота равна 3см.
А
Ответ: 2,5
Слайд 13Задача 4
В правильной треугольной пирамиде сторона основания равна 3см, боковые ребра
наклонены к плоскости основания под углом 60°. Найти радиус описанной около пирамиды сферы.
Слайд 18Вписанные шары
Шар называется вписанным в многогранник, а многогранник- описанным вокруг шара,
если плоскости всех граней касаются шара.
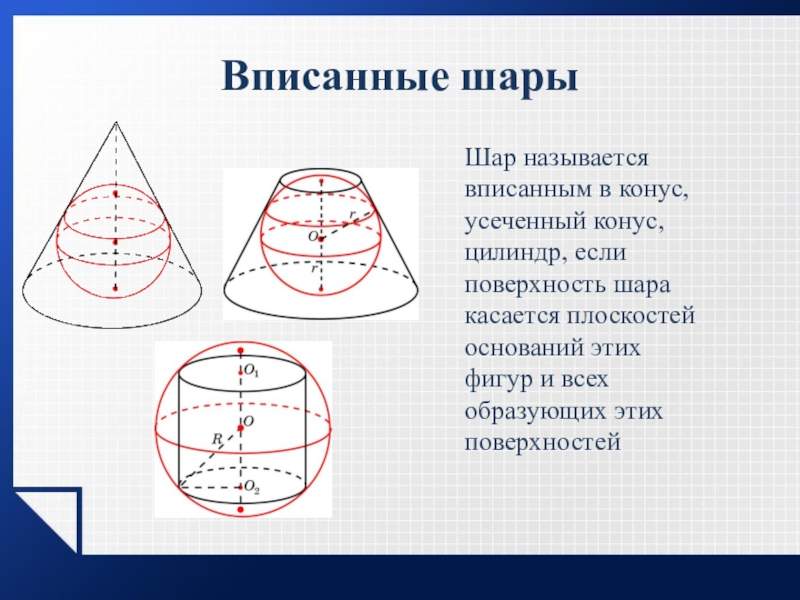
Слайд 19Вписанные шары
Шар называется вписанным в конус, усеченный конус, цилиндр, если поверхность
шара касается плоскостей оснований этих фигур и всех образующих этих поверхностей
Слайд 20Вписанные шары
Центр вписанного шара является
точка пересечения биссекторов всех внутренних двугранных
углов многогранника.
Слайд 21
Центр вписанной сферы является точка пересечения биссекторов всех внутренних двугранных
углов многогранника.
Слайд 22Шар, вписанный в призму
Для того, чтобы в призму можно было вписать
шар, необходимо и достаточно, чтобы в перпендикулярное сечение призмы можно было вписать окружность и чтобы высота призмы была равна диаметру этой окружности.
Слайд 23Шар, вписанный в призму
Шар можно вписать в прямую призму, если в
основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.
Центр вписанного шара лежит на середине высоты прямой призмы, проходящей через центры окружностей, вписанных в основание призмы.
Центр вписанного шара лежит на середине высоты прямой призмы, проходящей через центры окружностей, вписанных в основание призмы.
Слайд 24Шар, вписанный в конус
Центр вписанного в конус шара совпадает с точкой
пересечения высоты конуса с биссектрисой угла между любой образующей и плоскостью основания. В конус всегда можно вписать шар и его радиус выражается формулой
l
r
R
R
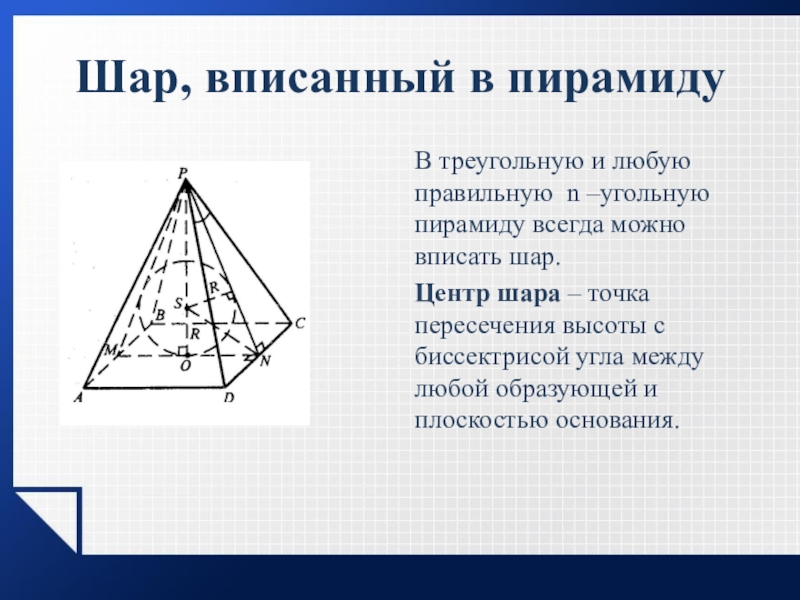
Слайд 25Шар, вписанный в пирамиду
В треугольную и любую правильную n –угольную пирамиду
всегда можно вписать шар.
Центр шара – точка пересечения высоты с биссектрисой угла между любой образующей и плоскостью основания.
Центр шара – точка пересечения высоты с биссектрисой угла между любой образующей и плоскостью основания.
Слайд 26Задача 1
В конус, образующая которого равна диаметру его основания и
равна 6, вписана сфера. Найти радиус сферы и расстояние от центра сферы до конической поверхности
Слайд 27Задача 2
Найти радиус шара, вписанного в пирамиду, основанием которой служит
ромб с диагоналями 6 см и 8 см, а высота пирамиды проходит через точку пересечения диагоналей основания и равна 1см.
