- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на темуСтереометрия. Важнейшие пространственные фигуры. Структура теории и задач
Содержание
- 1. Презентация по геометрии на темуСтереометрия. Важнейшие пространственные фигуры. Структура теории и задач
- 2. 06. 09. 2018Классная работа Стереометрия. Важнейшие пространственные фигуры.Структура теории и задач
- 3. I О геометрииСвоеобразие геометрии заключается
- 4. Во всяком подлинно геометрическом предложении, будь то
- 5. Наглядность, воображение принадлежат больше искусству,
- 6. Поэтому основное правило состоит в том, что,
- 7. Геометрия возникла из практических задач, её предложения
- 8. Установлено, что каждое десятое изобретение сделано
- 9. II О пространственных фигурахРаньше вы изучали главным
- 10. Каждый представляет, что такое плоскость или по
- 11. Вместе с каждой плоскостью в пространстве есть
- 12. Однако важнейшими в стереометрии являются пространственные фигуры,
- 13. Пирамидой называется многогранник, у которого одна грань
- 14. Простейшей среди всех пирамид (и даже среди
- 15. III О теоретической части курса. Весь курс
- 16. Курс 11 класса начинается главой IV о
- 17. Главы разбиты на параграфы (у них единая
- 18. Теоретический материал учебника разбит на две части
- 19. В каждом параграфе после теоретической части предложены
- 20. Определяя новое понятие, мы выделяем его (или
- 21. Если вы забыли какое-то определение, то найти
- 22. IV О задачахПосле вопросов для самоконтроля в
- 23. Различия в теоретическом стереометрическом материале базового
- 24. Задачи к параграфу обычно начинаются с небольшого
- 25. Но условия многих задач содержат и вопросы.
- 26. Ещё одна группа задач содержит вопросы другого
- 27. В условиях некоторых задач речь идёт о
- 28. Кроме задач к параграфам, в которых проверяется
- 29. Из всех многогранников в задачах чаще всего
- 30. Может оказаться, что у правильной треугольной пирамиды
- 31. V О рисункахОтличие рисунков, используемых в стереометрии
- 32. Плоскость изображается в виде параллелограмма (рис. 5,
- 33. Очень важно уметь правильно, наглядно изображать пространственные
- 34. Домашнее заданиеВведение стр. 7 - 12 : прочитать и выучить основные понятия.Выполнить: С – 1.
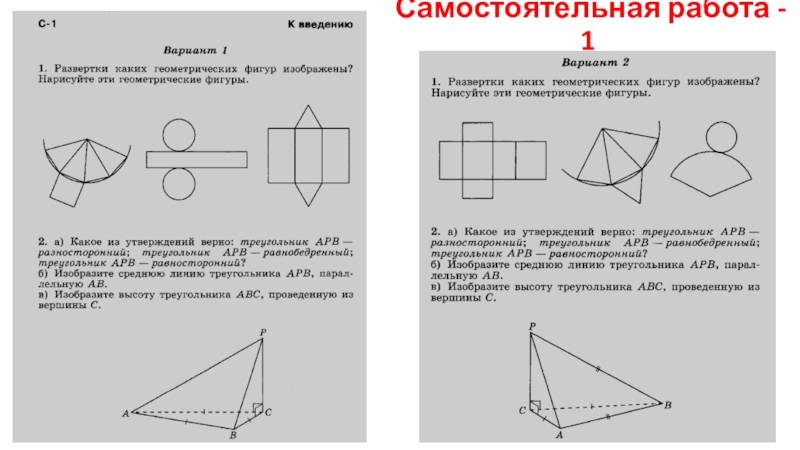
- 35. Самостоятельная работа - 1
06. 09. 2018Классная работа Стереометрия. Важнейшие пространственные фигуры.Структура теории и задач
Слайд 206. 09. 2018
Классная работа
Стереометрия.
Важнейшие пространственные фигуры.
Структура теории и задач
Слайд 3I О геометрии
Своеобразие геометрии заключается
в неразрывной связи живого воображения со строгой логикой.
Можно сказать, что геометрия в своей сути и есть пространственное воображение, пронизанное и организованное строгой логикой.
Можно сказать, что геометрия в своей сути и есть пространственное воображение, пронизанное и организованное строгой логикой.
Слайд 4Во всяком подлинно геометрическом предложении, будь то аксиома, определение, теорема или
задача, непременно присутствуют оба эти элемента: наглядная картина и строгая формулировка, строгий логический вывод.
Слайд 5Наглядность, воображение принадлежат больше искусству,
а строгая логика — привилегия науки. Сухость точного вывода и живость наглядной картины — геометрия соединяет в себе эти две противоположности. Так её и надо изучать: соединяя наглядные картины со строгими формулировками и доказательствами.
Слайд 6Поэтому основное правило состоит в том, что, встречаясь
с определением, теоремой или задачей, нужно прежде всего понять их содержание: представить наглядно, зарисовать или ещё лучше, хотя и труднее, вообразить то, о чём идёт речь. Ничего не старайтесь заучить, не нарисовав, не вообразив того, о чём написано в учебнике, не поняв, как это наглядное представление точно выражается в формулировке определения, теоремы или задачи.
Слайд 7Геометрия возникла из практических задач, её предложения выражают реальные факты и
находят многочисленные применения. В конечном счёте в основе всей техники так или иначе лежит геометрия, потому что она появляется везде, где нужна малейшая точность в определении формы и размеров. И технику, и инженеру, и рабочему, и архитектору, и модельеру необходимо геометрическое воображение.
Слайд 8Установлено, что каждое десятое изобретение сделано
с применением геометрии, за счёт выбора подходящей формы, удачного размещения и т. п. А ведь изобретений миллионы.
Математика, геометрия в частности, представляет собой могущественный инструмент познания природы и создания техники.
Математика, геометрия в частности, представляет собой могущественный инструмент познания природы и создания техники.
Слайд 9II О пространственных фигурах
Раньше вы изучали главным образом геометрию на плоскости
— планиметрию, а теперь будете заниматься геометрией в пространстве. Её называют стереометрией (от греческих слов «стереос» — пространственный, «метрео» — измеряю). Обращаясь к геометрии в пространстве — к стереометрии, мы предполагаем, что геометрия на плоскости — планиметрия — вам в основном известна.
Слайд 10Каждый представляет, что такое плоскость или по крайней мере конечный кусок
плоскости, как поверхность стола, доски и т. п. В планиметрии плоскость рассматривается сама по себе независимо от окружающего пространства. В стереометрии же плоскость — это фигура в пространстве, в котором много плоскостей. На каждой из них выполняются все положения планиметрии.
Слайд 11Вместе с каждой плоскостью в пространстве есть содержащиеся
в ней известные вам фигуры — точки, отрезки, треугольники, окружности и т. д. Основными свойствами этих фигур, теоремами о них, доказанными в планиметрии, мы будем пользоваться.
Слайд 12Однако важнейшими в стереометрии являются пространственные фигуры, тела, не лежащие ни
в какой плоскости. Простейшие знакомые вам тела изображены на рисунке 1:
а) шар; б) куб; в) параллелепипед; г) пирамида; д) призма; е) цилиндр; ж) конус. Определения шара, призмы, цилиндра и конуса мы дадим позже, а сейчас напомним, что куб — это многогранник, у которого шесть граней, и все они квадраты.
Прямоугольный параллелепипед — это многогранник, у которого шесть граней, и все они прямоугольники. А вообще параллелепипед — это многогранник, у которого шесть граней, и все они параллелограммы.
а) шар; б) куб; в) параллелепипед; г) пирамида; д) призма; е) цилиндр; ж) конус. Определения шара, призмы, цилиндра и конуса мы дадим позже, а сейчас напомним, что куб — это многогранник, у которого шесть граней, и все они квадраты.
Прямоугольный параллелепипед — это многогранник, у которого шесть граней, и все они прямоугольники. А вообще параллелепипед — это многогранник, у которого шесть граней, и все они параллелограммы.
Слайд 13Пирамидой называется многогранник, у которого одна грань — какой-либо многоугольник, а
остальные грани — треугольники с общей вершиной. Первая грань называется основанием пирамиды, остальные же называются боковыми гранями; их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются её рёбрами, причём рёбра, сходящиеся в вершине, называются боковыми. Если основание пирамиды — n-угольник, то пирамида называется n-угольной.
Слайд 14Простейшей среди всех пирамид (и даже среди всех многогранников) является треугольная
пирамида, которую называют также тетраэдром, т. е. четырёхгранником (рис. 2). У тетраэдра четыре грани, и все они треугольники.
Пирамида называется правильной, если её основание — правильный многоугольник, а все боковые рёбра равны (рис. 3). Знаменитые египетские пирамиды — правильные четырёхугольные.
Пирамида называется правильной, если её основание — правильный многоугольник, а все боковые рёбра равны (рис. 3). Знаменитые египетские пирамиды — правильные четырёхугольные.
Рис. 3
Слайд 15III О теоретической части курса.
Весь курс разбит на шесть глав
(по три на каждый класс). Глава I вводная, а центральной и основной в курсе 10 класса является глава II, где изучается перпендикулярность и параллельность прямых и плоскостей, а также расстояния и углы. (Эту главу можно назвать «строительной геометрией», поскольку изучаемые в ней вопросы играют главную роль в строительстве. Завершает курс 10 класса глава III, в которой рассказано о важнейших пространственных фигурах — сфере и шаре, цилиндрах и конусах. Последний параграф этой главы (§ 20) посвящён геометрии окружности.
Слайд 16Курс 11 класса начинается главой IV о многогранниках
и симметрии фигур. В главе V речь идёт об измерении объёмов тел и площадей их поверхностей.
В последней же — главе VI — о координатах и векторах рассматриваются такие методы геометрии, которые возникли значительно позднее. Завершает книгу рассказ о современной геометрии.
В последней же — главе VI — о координатах и векторах рассматриваются такие методы геометрии, которые возникли значительно позднее. Завершает книгу рассказ о современной геометрии.
Слайд 17Главы разбиты на параграфы (у них единая нумерация),
а параграфы — на пункты (у пунктов двойная нумерация: например, п. 17.3 — это третий пункт из § 17).
Пункты, относящиеся одновременно и к базовому и к углублённому уровню образовательного стандарта по математике набраны чёрным цветом на цветной плашке таким образом: 24.5 .
Пункты ознакомительного характера (как, например, в заключении) набраны так: 2.1 .
Пункты, относящиеся только к углублённому уровню, обозначены таким образом: 29.5 .
Пункты, относящиеся одновременно и к базовому и к углублённому уровню образовательного стандарта по математике набраны чёрным цветом на цветной плашке таким образом: 24.5 .
Пункты ознакомительного характера (как, например, в заключении) набраны так: 2.1 .
Пункты, относящиеся только к углублённому уровню, обозначены таким образом: 29.5 .
Слайд 18Теоретический материал учебника разбит на две части — основную
и дополнительную.
Основная часть, во-первых, содержит теоретические сведения (аксиомы, определения, теоремы), которые надо твёрдо усвоить и уметь применять при решении задач. Во-вторых, к основной части относится материал, в котором рассказано о значении наиболее важных геометрических результатов, о различных применениях стереометрии в других науках, технике, искусстве, быту, об истории геометрии. С этим материалом, отмеченным значками ▲ (начало) и ▼ (конец), следует ознакомиться. Он поможет вам понять роль геометрии и её место в современной культуре.
Основная часть, во-первых, содержит теоретические сведения (аксиомы, определения, теоремы), которые надо твёрдо усвоить и уметь применять при решении задач. Во-вторых, к основной части относится материал, в котором рассказано о значении наиболее важных геометрических результатов, о различных применениях стереометрии в других науках, технике, искусстве, быту, об истории геометрии. С этим материалом, отмеченным значками ▲ (начало) и ▼ (конец), следует ознакомиться. Он поможет вам понять роль геометрии и её место в современной культуре.
Слайд 19В каждом параграфе после теоретической части предложены вопросы для самоконтроля. Очень
важно самому подготовить ответы на них — тогда на уроке вы будете чувствовать себя уверенней.
Слайд 20Определяя новое понятие, мы выделяем его (или всё определение) полужирным шрифтом
(например, куб). Формулировки аксиом, теорем и их следствий набраны также полужирным шрифтом. Остальные же предложения, на которые надо обратить особое внимание, выделены курсивом. Начало доказательства выделено словом доказательство или значком □. Окончание доказательства утверждения обозначается значком ■. Так же обозначается конец замечания.
Слайд 21Если вы забыли какое-то определение, то найти его в учебнике вам
поможет предметный указатель в конце книги. Там же помещён список дополнительной литературы к учебнику.
Слайд 22IV О задачах
После вопросов для самоконтроля в каждом параграфе (кроме чисто
теоретического § 25) идут задачи к этому параграфу. У задач к параграфу двойная нумерация: сначала указан номер параграфа, а затем номер задачи в этом параграфе. Например, задача 20.15 — это пятнадцатая задача к § 20. Более трудные задачи отмечены значком *.
Слайд 23Различия в теоретическом стереометрическом материале базового
и углублённого уровней незначительны. Существенное различие этих уровней в задачном материале: базовому уровню соответствуют более простые задачи (их номера чёрного цвета), углублённому уровню — более сложные задачи (их номера красного цвета).
У некоторых задач, отмеченных как базовые и разбитых на пункты а), б), в) и т. д., часть пунктов соответствует базовому уровню — они отмечены чёрным цветом, а остальные пункты углублённого уровня — они отмечены красным цветом.
У некоторых задач, отмеченных как базовые и разбитых на пункты а), б), в) и т. д., часть пунктов соответствует базовому уровню — они отмечены чёрным цветом, а остальные пункты углублённого уровня — они отмечены красным цветом.
Слайд 24Задачи к параграфу обычно начинаются с небольшого числа задач, дополняющих теорию
этого параграфа. Они отделены от других задач к параграфу. На такие задачи возможны в дальнейшем ссылки наравне с теоретическим текстом.
О том, что надо сделать, решая задачу, в большинстве условий задач сказано в утвердительной форме: Нарисуйте, Вычислите, Докажите, Постройте, Найдите границы и т. п.
О том, что надо сделать, решая задачу, в большинстве условий задач сказано в утвердительной форме: Нарисуйте, Вычислите, Докажите, Постройте, Найдите границы и т. п.
Слайд 25Но условия многих задач содержат и вопросы. Есть задачи, где ставятся
такие вопросы: «Как вычислить...?», «Как найти...!», «Как построить...!» и т. п. В этих задачах главное — составить план решения, может быть, даже алгоритм решения. После этого можно получить ответ в виде формулы, введя необходимые величины.
Слайд 26Ещё одна группа задач содержит вопросы другого типа: «Есть ли...?», «Можно
ли...?», «Может ли быть...?», «Верно ли...?», «Какой по форме...?», «Какого вида...?» и т. п. Это задачи исследовательского характера. В условиях таких задач возможна некая неопределённость, незавершённость, даже неоднозначность. Возможно и отсутствие решения этих задач, что вы должны выяснить.
Слайд 27В условиях некоторых задач речь идёт о реальных бытовых ситуациях: например,
в задаче 11.4 о часовых стрелках или в задаче 27.33 об арбузах. При решении таких задач прикладной геометрии их условие ещё надо перевести на математический язык.
Слайд 28Кроме задач к параграфам, в которых проверяется усвоение содержания именно этого
параграфа, есть ещё задачи к главам. Эти задачи труднее задач к параграфам, они многоплановы и имеют итоговый характер.
В задачах к главам I, II, VI имеется рубрика «Применяем компьютер». Решая задачи этой рубрики, используйте, например, среду «Живая математика», которую можно найти по адресу: http:www.uchportal.ru/lоаd/24-1-0-2276.
В задачах к главам I, II, VI имеется рубрика «Применяем компьютер». Решая задачи этой рубрики, используйте, например, среду «Живая математика», которую можно найти по адресу: http:www.uchportal.ru/lоаd/24-1-0-2276.
Слайд 29Из всех многогранников в задачах чаще всего рассматриваются пирамиды — треугольные
(тетраэдры) и четырёхугольные. Для удобства мы обозначаем их соответственно РАВС и РАВСD, считая, что основанием пирамиды является треугольник АВС или четырёхугольник АВСD, а вершиной — точка Р.
В основании правильной треугольной пирамиды РАВС лежит равносторонний (правильный) треугольник АВС, а боковые рёбра её равны: РА = РВ = РС (рис. 4, а).
В основании правильной треугольной пирамиды РАВС лежит равносторонний (правильный) треугольник АВС, а боковые рёбра её равны: РА = РВ = РС (рис. 4, а).
Рис. 4
Слайд 30Может оказаться, что у правильной треугольной пирамиды РАВС боковые рёбра равны
сторонам основания, т. е. в таком тетраэдре все рёбра равны. Тетраэдр, у которого все рёбра равны, называется правильным тетраэдром; все его грани — правильные треугольники (рис. 4, б). А у правильной треугольной пирамиды заведомо лишь одна грань — основание — правильный треугольник. Боковые же её грани — равнобедренные треугольники.
Отметим ещё, что в основании правильной четырёхугольной пирамиды лежит квадрат АВСD.
Отметим ещё, что в основании правильной четырёхугольной пирамиды лежит квадрат АВСD.
Рис. 4
Слайд 31V О рисунках
Отличие рисунков, используемых в стереометрии (например, рисунков 1—3), от
тех, какими иллюстрируется курс планиметрии, состоит в том, что на плоскости рисунка (в книге, в тетради, на доске) изображены не только плоские, но и пространственные фигуры. Основные правила и приёмы таких изображений будут обоснованы в курсе стереометрии.
Рис. 3
Слайд 32Плоскость изображается в виде параллелограмма (рис. 5, а), а иногда в
виде произвольной области (рис. 5, б).
Параллельные отрезки (как и прямые) изображаются параллельными отрезками (как при изображении куба или призмы на рисунке 1, б, в, д).
Середина отрезка изображается как середина его изображения, которое тоже является отрезком.
Параллельные отрезки (как и прямые) изображаются параллельными отрезками (как при изображении куба или призмы на рисунке 1, б, в, д).
Середина отрезка изображается как середина его изображения, которое тоже является отрезком.
Рис. 1
Слайд 33Очень важно уметь правильно, наглядно изображать пространственные фигуры и, наоборот, посмотрев
на рисунок, представить себе форму пространственной фигуры, изображённой на нём. Это трудно, но этому можно научиться.
Слайд 34Домашнее задание
Введение стр. 7 - 12 :
прочитать и выучить основные
понятия.
Выполнить: С – 1.
Выполнить: С – 1.