- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
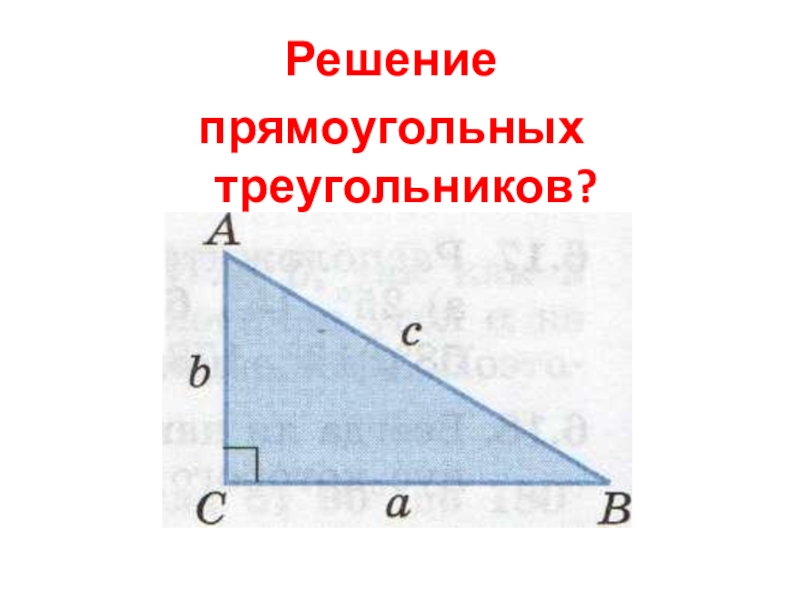
Презентация, доклад по геометрии на темуРешение прямоугольных треугольников
Содержание
- 1. Презентация по геометрии на темуРешение прямоугольных треугольников
- 2. BCAПрямоугольным называется треугольник, у которого Катеты –
- 3. Решение прямоугольных треугольников?
- 4. Какие элементы прямоугольного треугольника были известны?Гипотенуза и
- 5. Нахождение неизвестных элементов прямоугольного треугольника по известным
- 6. Теоретический материал:Определение синуса острого угла.Теорема Пифагора.Следствия прямоугольного треугольника.
- 7. Слайд 7
- 8. cbaТеорема Пифагора:В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.c² = a² + b²
- 9. cbaСледствие о сумме острых углов в прямоугольном
- 10. cbaСледствие о катете в прямоугольном треугольнике :Катет
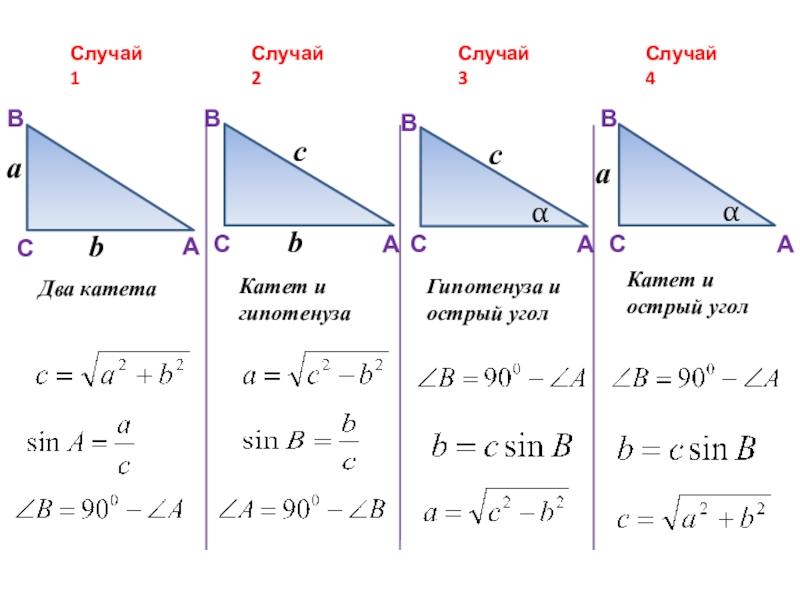
- 11. CBbcACBabCBaαCBcαAAAДва катетаКатет и гипотенузаКатет и острый уголГипотенуза и острый уголСлучай 1Случай 2Случай 4Случай 3
- 12. Случай 1 Два катета Дано: а; b.
- 13. Случай 2 Катет и гипотенуза Дано: с;
- 14. Случай 3 Гипотенуза и острый угол Дано:
- 15. Случай 4 Катет и острый угол Дано:
- 16. Решение задачстр. 104 – 105№ 6.32 (а,
- 17. № 6.32(а)Дано: а = 1; b =
- 18. № 6.32(в) Дано: а = 2; ∠А
- 19. Дано: с = 12; ∠А =
- 20. № 6. 33(а)Дано: ∆АВС; АВ = АС
- 21. № 6. 33( в)Дано: ∆АВС; АВ =
- 22. № 6. 33(д)Дано: ∆АВС; АВ = АС
- 23. Прямоугольный треугольник имеет широкое применение в повседневной
- 24. пирамида Кукулькана («Оперённый змей»), Юкатан, Мексика
- 25. 55,5 м31 м52о?Цель – вычислить высоту пирамиды
- 26. к а т е ткатетгипотенузапротиволежащий31 м52о?
- 27. 3252о?ACABsin ∠В =ВСА25 м
- 28. Домашнее заданиестр. 104 – 105№ 6.32 (б,
- 29. № 6. 33(б)Дано: ∆АВС; АВ = АС
- 30. Спасибо за урок
- 31. na –uroke. in. ua
BCAПрямоугольным называется треугольник, у которого Катеты – это Гипотенуза - это Элементы треугольника – это Что означает термин «решить треугольник (прямоугольный)»?один из его углов прямой, а два других угла острые. взаимно перпендикулярные стороны.третья сторона. стороны и
Слайд 2B
C
A
Прямоугольным называется треугольник, у которого
Катеты – это
Гипотенуза - это
Элементы треугольника – это
Что означает термин «решить треугольник (прямоугольный)»?
один из его углов прямой, а два других угла острые.
взаимно перпендикулярные стороны.
третья сторона.
стороны и углы.
Слайд 4Какие элементы прямоугольного треугольника были известны?
Гипотенуза и катет.
Какие еще элементы треугольника
мы нашли?
Второй катет и острые углы.
Слайд 5Нахождение неизвестных элементов прямоугольного треугольника по известным двум его элементам называется
решением прямоугольного треугольника
Решить прямоугольный треугольник — значит вычислить все его стороны и углы по каким-либо данным, определяющим этот треугольник.
Слайд 6Теоретический материал:
Определение синуса острого угла.
Теорема Пифагора.
Следствия прямоугольного треугольника.
Слайд 7 sin A = а
: с ; sin B = b : с.
т. е. синус острого угла прямоугольного треугольника равен отношению катета, лежащего против этого угла, и гипотенузы треугольника.
Короче говорят так: синус равен отношению противолежащего катета к гипотенузе.
Слайд 8c
b
a
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
c² =
a² + b²
Слайд 9c
b
a
Следствие о сумме острых углов в прямоугольном треугольнике :
Сумма острых углов
прямоугольного треугольника равна 90°.
∠А + ∠В = 90°
А
В
С
Слайд 10c
b
a
Следствие о катете в прямоугольном треугольнике :
Катет прямоугольного треугольника, лежащий против
угла в 300 равен половине гипотенузы.
А
В
С
300
Слайд 11C
B
b
c
A
C
B
a
b
C
B
a
α
C
B
c
α
A
A
A
Два катета
Катет и гипотенуза
Катет и острый угол
Гипотенуза и острый угол
Случай 1
Случай
2
Случай 4
Случай 3
Слайд 12Случай 1
Два катета
Дано: а; b.
Найти: с; ∠А; ∠В.
Решение:
По теореме Пифагора:
c² = a² + b²;
По определению: sin A = а : с;
По следствию: ∠В = 90° - ∠А.
По определению: sin A = а : с;
По следствию: ∠В = 90° - ∠А.
A
В
С
а
b
c
Слайд 13Случай 2
Катет и гипотенуза
Дано: с; b.
Найти: а; ∠А; ∠В.
Решение:
По теореме
Пифагора: а² = с² - b²;
По определению: sin A = а : с;
По следствию: ∠В = 90° - ∠А.
По определению: sin A = а : с;
По следствию: ∠В = 90° - ∠А.
A
В
С
а
b
c
Слайд 14Случай 3
Гипотенуза и острый угол
Дано: с; ∠А .
Найти: а; b;
∠В.
Решение:
По следствию: ∠В = 90° - ∠А ;
По определению: sin A = а : с ⇒ а = с sin A ;
По определению: sin В = b : с ⇒ b = с sin B .
Решение:
По следствию: ∠В = 90° - ∠А ;
По определению: sin A = а : с ⇒ а = с sin A ;
По определению: sin В = b : с ⇒ b = с sin B .
A
В
С
а
b
c
Слайд 15Случай 4
Катет и острый угол
Дано: а; ∠А .
Найти: с; b;
∠В.
Решение:
По следствию: ∠В = 90° - ∠А ;
По определению: sin A = а : с ⇒ с = а : sin A ;
По теореме Пифагора: b² = с² - a² .
Решение:
По следствию: ∠В = 90° - ∠А ;
По определению: sin A = а : с ⇒ с = а : sin A ;
По теореме Пифагора: b² = с² - a² .
A
В
С
а
b
c
Слайд 16Решение задач
стр. 104 – 105
№ 6.32 (а, в, д); № 6.
33 (а, в, д); № 6.34; № 6. 35; № 6. 36; № 6.38.
Слайд 17№ 6.32(а)
Дано: а = 1; b = 2.
Найти: с; ∠А;
∠В.
Решение:
По теореме Пифагора: c² = a² + b²;
с² = 1² + 2² = 5; с = √5
По определению: sin A = 1 : √5 ; ∠А≈ 27°
По следствию: ∠В = 90° - 27°≈ 63° .
Ответ: с = √5; ∠А≈ 27° ; ∠В ≈ 63° .
Решение:
По теореме Пифагора: c² = a² + b²;
с² = 1² + 2² = 5; с = √5
По определению: sin A = 1 : √5 ; ∠А≈ 27°
По следствию: ∠В = 90° - 27°≈ 63° .
Ответ: с = √5; ∠А≈ 27° ; ∠В ≈ 63° .
A
В
С
а
b
c
Слайд 18№ 6.32(в)
Дано: а = 2; ∠А = 35°.
Найти: с;
b; ∠В.
Решение:
По следствию: ∠В = 90° - 35°= 55° ;
По определению: sin A = а : с ⇒ с = 2 : sin 35°= 2 : 0,574 ≈ 3,48;
По теореме Пифагора: b² = 3,48² - 2² ; b≈ 2, 86.
Ответ: ∠В = 55°; с ≈ 3,48; b≈ 2, 86.
Решение:
По следствию: ∠В = 90° - 35°= 55° ;
По определению: sin A = а : с ⇒ с = 2 : sin 35°= 2 : 0,574 ≈ 3,48;
По теореме Пифагора: b² = 3,48² - 2² ; b≈ 2, 86.
Ответ: ∠В = 55°; с ≈ 3,48; b≈ 2, 86.
A
В
С
а
b
c
Слайд 19
Дано: с = 12; ∠А = 44° .
Найти: а;
b; ∠В.
Решение:
По следствию: ∠В = 90° - 44° = 46°;
По определению: а = с sin A ; а = 12 sin44° = 12 ∙ 0,695 ≈ 8, 34;
По определению: b = с sin B .
b = 12 sin46° = 12 ∙ 0,719 ≈ 8, 63.
Ответ: : ∠В = 46°; а ≈ 8, 34; b ≈ 8, 63.
Решение:
По следствию: ∠В = 90° - 44° = 46°;
По определению: а = с sin A ; а = 12 sin44° = 12 ∙ 0,695 ≈ 8, 34;
По определению: b = с sin B .
b = 12 sin46° = 12 ∙ 0,719 ≈ 8, 63.
Ответ: : ∠В = 46°; а ≈ 8, 34; b ≈ 8, 63.
A
В
С
а
b
c
№ 6.32(д)
Слайд 20№ 6. 33(а)
Дано: ∆АВС;
АВ = АС = 13; ВС =
10 - основание;
Найти: ∠А ;∠В; ∠С.
Решение:
1.BD ² = 13² - 5² = 169 – 25 = 144; ВD = 12.
2. sinВ = sin С = 12 : 13 ≈ 0,923; ∠В = ∠С ≈67°.
3. ∠А = 180° – (∠В +∠С) ≈ 180° - 134° ≈ 46°.
Ответ: ∠В = ∠С ≈67°; ∠А ≈46°.
Найти: ∠А ;∠В; ∠С.
Решение:
1.BD ² = 13² - 5² = 169 – 25 = 144; ВD = 12.
2. sinВ = sin С = 12 : 13 ≈ 0,923; ∠В = ∠С ≈67°.
3. ∠А = 180° – (∠В +∠С) ≈ 180° - 134° ≈ 46°.
Ответ: ∠В = ∠С ≈67°; ∠А ≈46°.
А
В
С
D
13
13
10
Слайд 21№ 6. 33( в)
Дано: ∆АВС;
АВ = АС ; ВС =
10 - основание; ∠В =36°.
Найти: АВ ; АС ; ∠В; ∠С.
Решение:
∠BAD = 90° - 36° = 54°.
АВ = BD : sin BAD; АВ = 5 : sin 54°≈ 5 : 0,809 ≈ ≈ 6,18
Ответ: ∠А = 108°; АВ = АС ≈ 6,18.
Найти: АВ ; АС ; ∠В; ∠С.
Решение:
∠BAD = 90° - 36° = 54°.
АВ = BD : sin BAD; АВ = 5 : sin 54°≈ 5 : 0,809 ≈ ≈ 6,18
Ответ: ∠А = 108°; АВ = АС ≈ 6,18.
А
В
С
D
10
Слайд 22№ 6. 33(д)
Дано: ∆АВС;
АВ = АС = 8; ВС -
основание;
∠В = ∠С = 36°;
Найти: ∠А ; ВС.
Решение:
∠А = 180° – (∠В +∠С) = 180° - 72° = 108°.
∠BAD = 108° : 2 = 54°.
BD = АВ sin BAD = 8 sin 54° = 8 ∙ 0,809 ≈ 6,47.
4. ВС ≈ 12,9
Ответ: ВС ≈ 12,9; ∠А ≈ 108°.
∠В = ∠С = 36°;
Найти: ∠А ; ВС.
Решение:
∠А = 180° – (∠В +∠С) = 180° - 72° = 108°.
∠BAD = 108° : 2 = 54°.
BD = АВ sin BAD = 8 sin 54° = 8 ∙ 0,809 ≈ 6,47.
4. ВС ≈ 12,9
Ответ: ВС ≈ 12,9; ∠А ≈ 108°.
А
В
С
D
8
8
10
Слайд 23Прямоугольный треугольник имеет широкое применение в повседневной жизни – многие геометрические
и практические задачи сводятся к вычислению элементов прямоугольного треугольника, другими словами к решению прямоугольного треугольника.
Слайд 29№ 6. 33(б)
Дано: ∆АВС;
АВ = АС ; ВС = 10
- основание; ∠А =52°.
Найти: АВ ; АС ; ∠В; ∠С.
Решение:
∠В = ∠С = (180°- ∠А ) : 2 = (180°- 52° ) : 2 = 64°.
∠BAD = 90° – 64° = 26°
АВ = BD : sin BAD; АВ = 5: sin 26°≈ 5 : 0,438 ≈11,4
Ответ: ∠В = ∠С ≈ 26°; АВ = АС ≈ 11,4.
Найти: АВ ; АС ; ∠В; ∠С.
Решение:
∠В = ∠С = (180°- ∠А ) : 2 = (180°- 52° ) : 2 = 64°.
∠BAD = 90° – 64° = 26°
АВ = BD : sin BAD; АВ = 5: sin 26°≈ 5 : 0,438 ≈11,4
Ответ: ∠В = ∠С ≈ 26°; АВ = АС ≈ 11,4.
А
В
С
D
10
