- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на темуИзмерение вписанных углов (9 класс)
Содержание
- 1. Презентация по геометрии на темуИзмерение вписанных углов (9 класс)
- 2. 30. 03. 18Классная работа Измерение вписанных углов.
- 3. Вопросы для самоконтроля Как вводят градусную меру
- 4. Градусное измерение дуг окружности позволяет решить разнообразные
- 5. Угол, вершина которого лежит на окружности, а
- 6. Углом, вписанным в окружность, называется угол между
- 7. Теорема (об измерении вписанного угла). Угол,
- 8. Проведем тогда радиус ОА.Δ ОАВ - равнобедренный,
- 9. 2 случай: О ∊ внутри ∠ АВС
- 10. 3 случай: О ∊ вне ∠ АВС
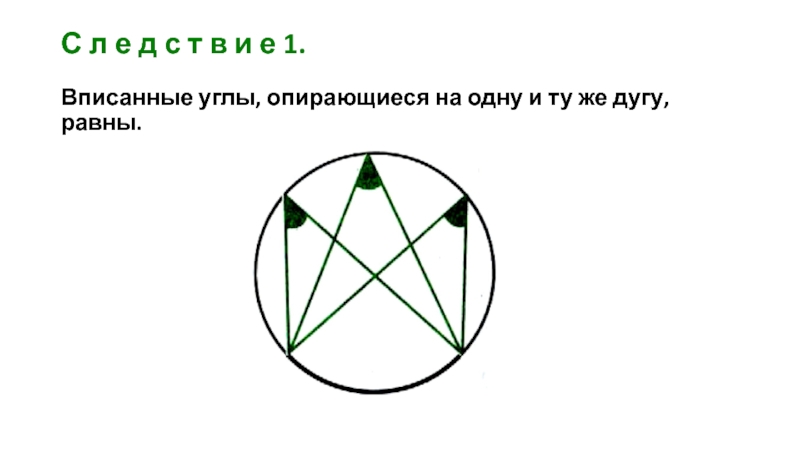
- 11. С л е д с т в
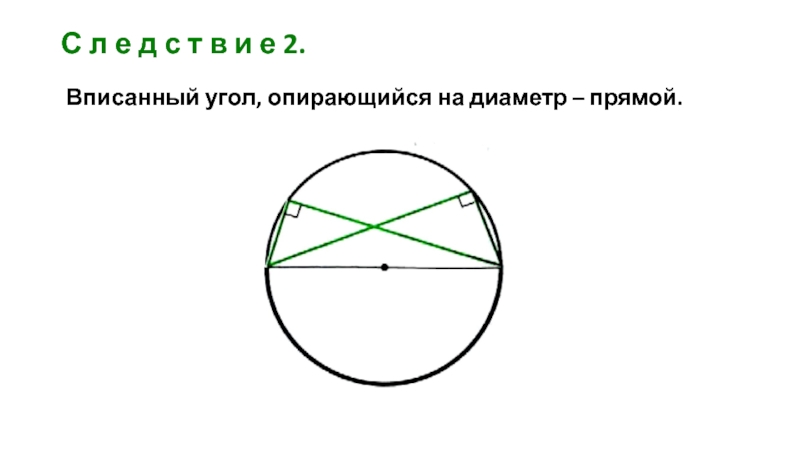
- 12. С л е д с т в
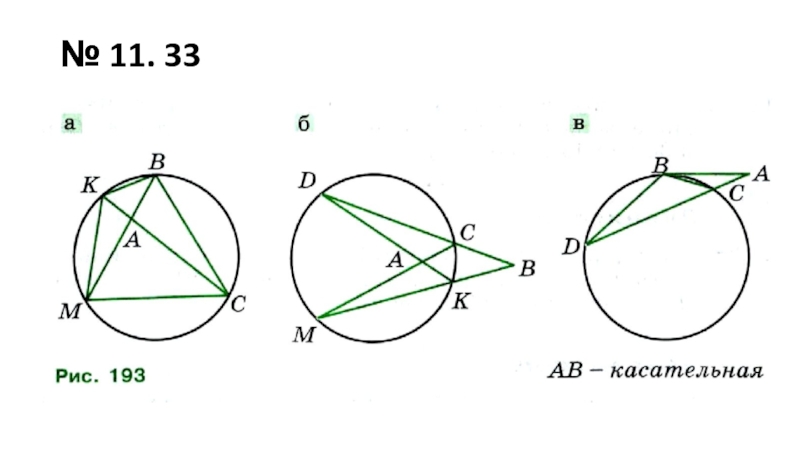
- 13. № 11. 33
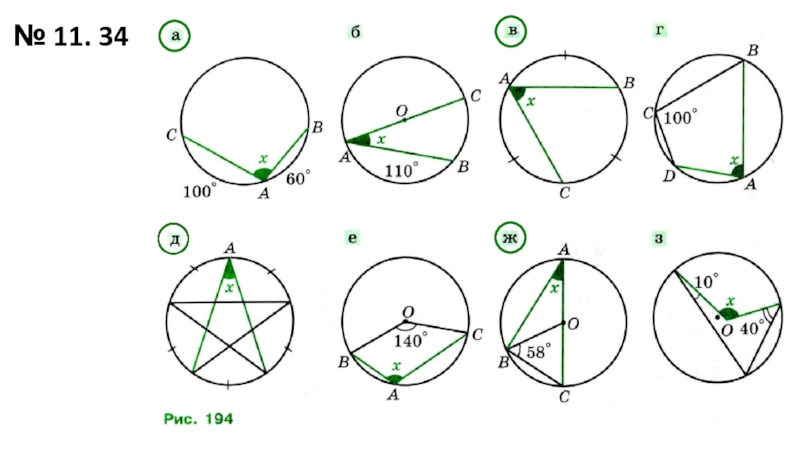
- 14. № 11. 34
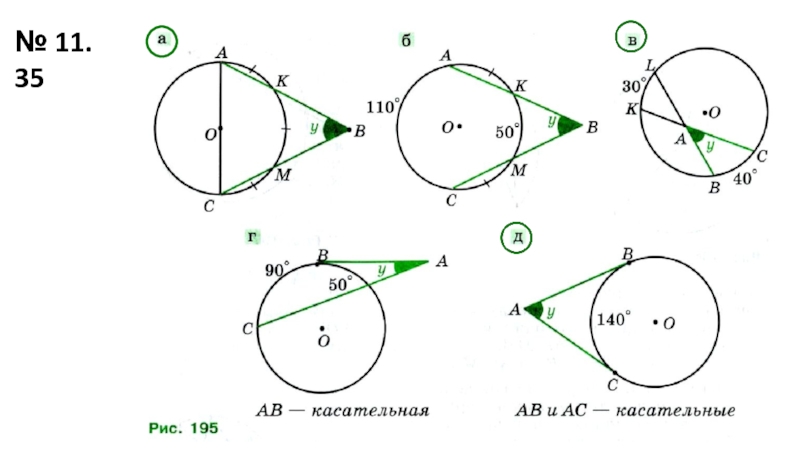
- 15. № 11. 35
- 16. Домашнее заданиеn. 11. 4№ 11. 34 (б, г, е, з); № 11. 35 (б, г)
Слайд 3Вопросы для самоконтроля
Как вводят градусную меру дуги?
Сколько градусов имеет четверть
Если дуга АВ имеет градусную меру α°, то пишут: …?
4. Как определяется равенство двух дуг одной
окружности?
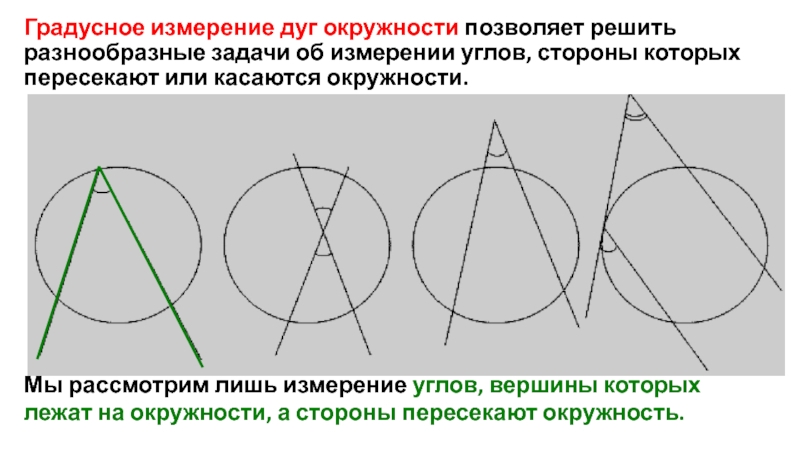
Слайд 4Градусное измерение дуг окружности позволяет решить разнообразные задачи об измерении углов,
Мы рассмотрим лишь измерение углов, вершины которых лежат на окружности, а стороны пересекают окружность.
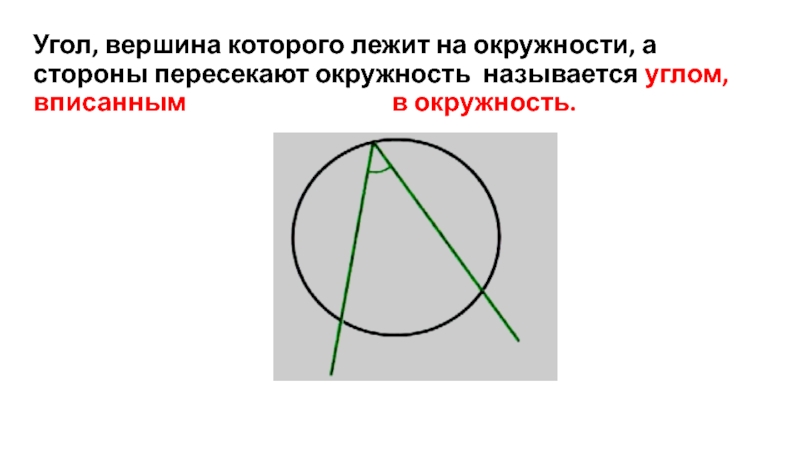
Слайд 5Угол, вершина которого лежит на окружности, а стороны пересекают окружность называется
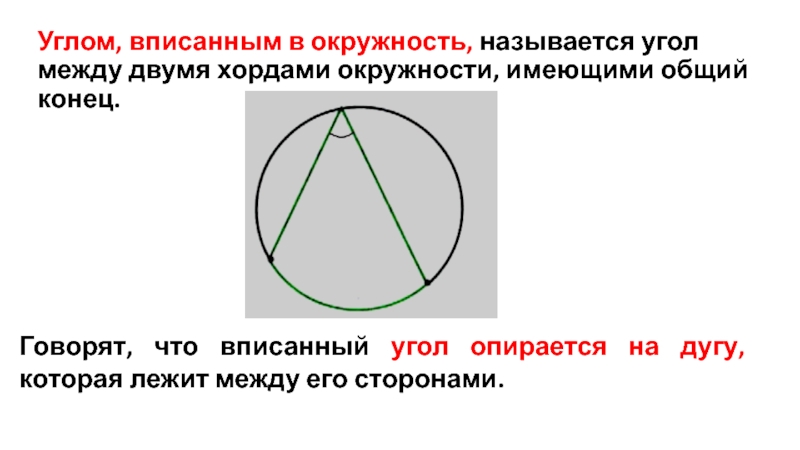
Слайд 6Углом, вписанным в окружность, называется угол между двумя хордами окружности, имеющими
Говорят, что вписанный угол опирается на дугу, которая лежит между его сторонами.
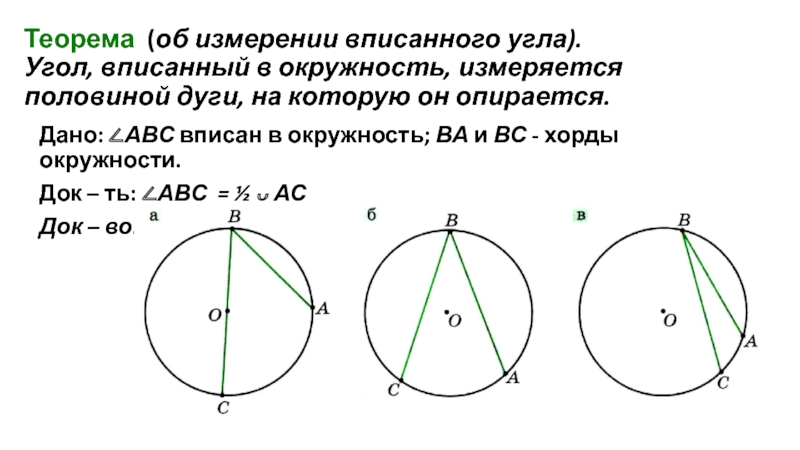
Слайд 7Теорема (об измерении вписанного угла). Угол, вписанный в окружность, измеряется половиной
Дано: ∠АВС вписан в окружность; ВА и ВС - хорды окружности.
Док – ть: ∠АВС = ½ ᴗ АС
Док – во:
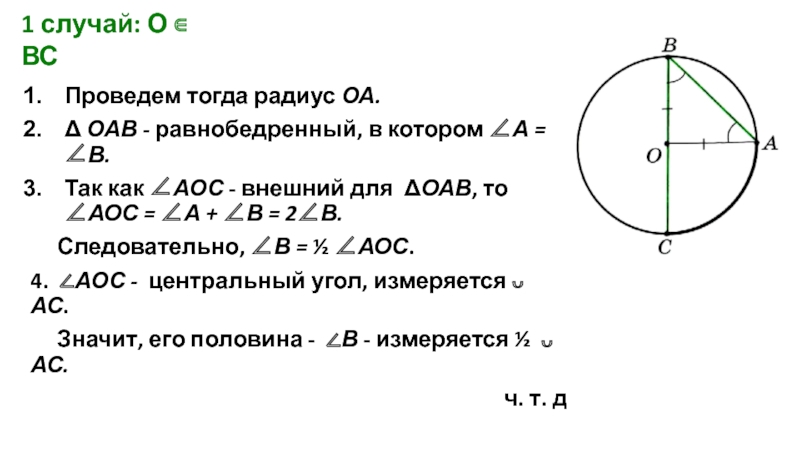
Слайд 8Проведем тогда радиус ОА.
Δ ОАВ - равнобедренный, в котором ∠А =
Так как ∠АОС - внешний для ΔОАВ, то ∠АОС = ∠А + ∠В = 2∠В.
Следовательно, ∠В = ½ ∠АОС.
4. ∠АОС - центральный угол, измеряется ᴗ АС.
Значит, его половина - ∠В - измеряется ½ ᴗ АС.
ч. т. д
1 случай: О ∊ ВС
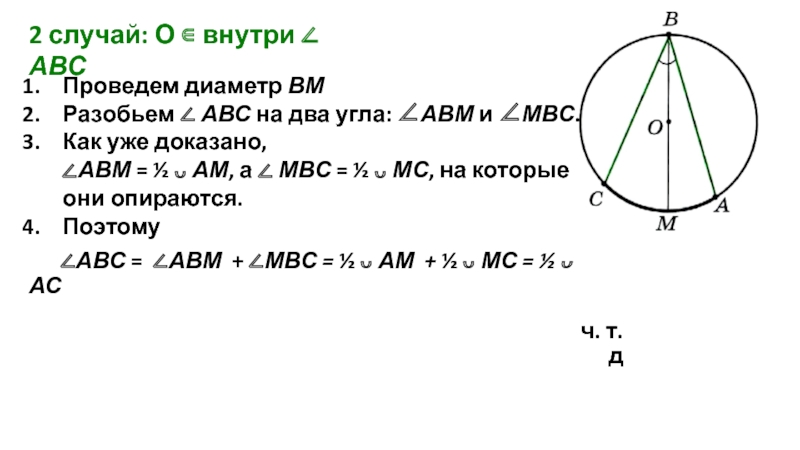
Слайд 92 случай: О ∊ внутри ∠ АВС
Проведем диаметр ВМ
Разобьем
Как уже доказано, ∠АВМ = ½ ᴗ АМ, а ∠ МВС = ½ ᴗ МС, на которые они опираются.
Поэтому
∠АВС = ∠АВМ + ∠МВС = ½ ᴗ АМ + ½ ᴗ МС = ½ ᴗ АС
ч. т. д
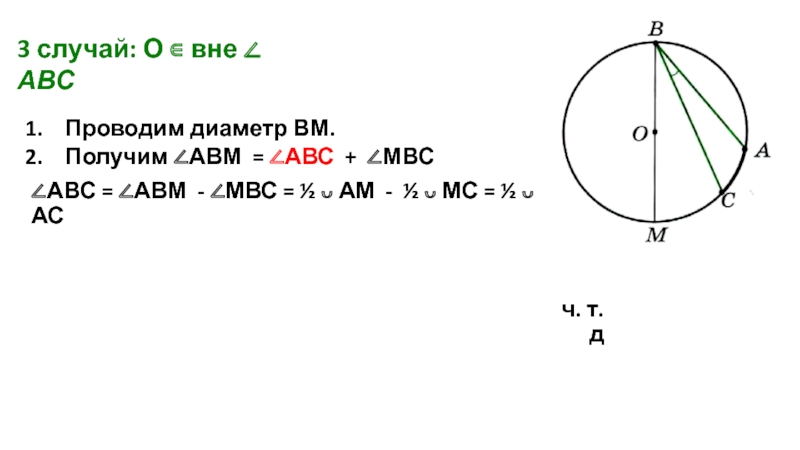
Слайд 103 случай: О ∊ вне ∠ АВС
Проводим диаметр ВМ.
Получим
∠АВС = ∠АВМ - ∠МВС = ½ ᴗ АМ - ½ ᴗ МС = ½ ᴗ АС
ч. т. д