- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Вычисление углов в пространстве, 11 класс
Содержание
- 1. Презентация по геометрии на тему Вычисление углов в пространстве, 11 класс
- 2. "Мастерство - это то, чего можно добиться" А.С. Макаренко
- 3. Цели урока: Показать, как используется скалярное
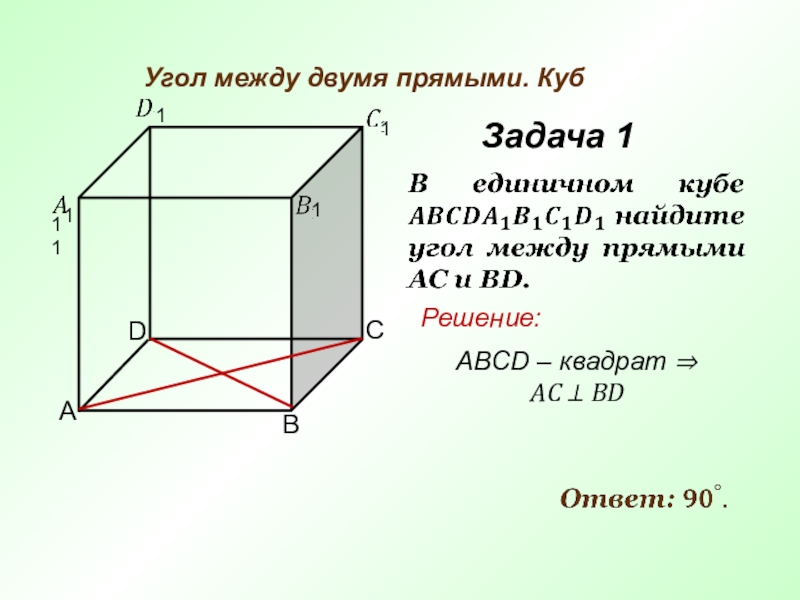
- 4. 11Задача 1 Угол между двумя прямыми. Куб ABCD – квадрат ⇒ AC ⊥ BDРешение:1111
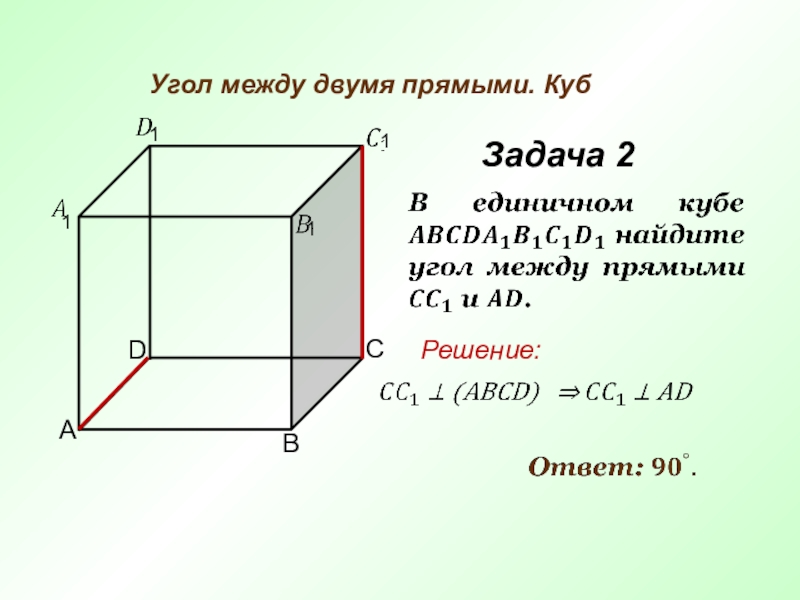
- 5. Угол между двумя прямыми. КубЗадача 2 ACBD Решение: 1111
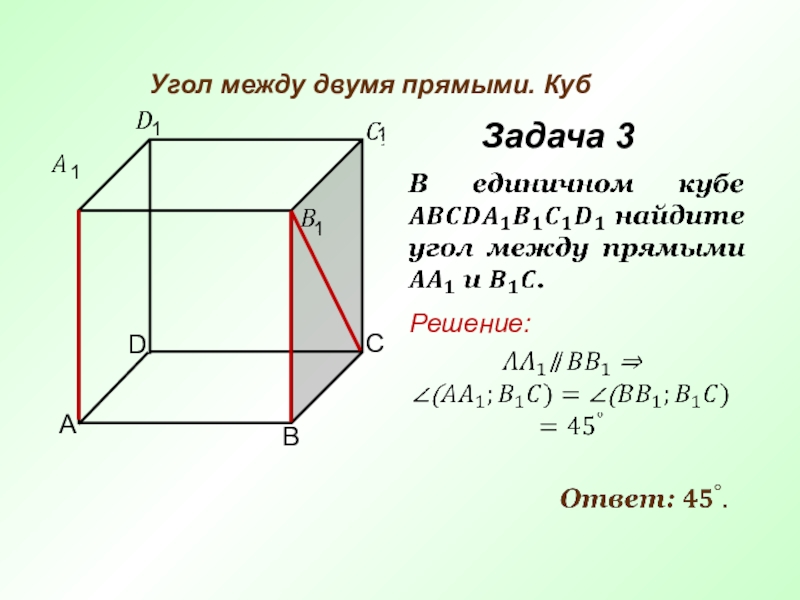
- 6. Угол между двумя прямыми. КубЗадача 3 Решение: 1111
- 7. Угол между двумя прямыми. КубЗадача 4 Решение: 1111
- 8. Повторяем теорию:Как находят координаты вектора, если известны
- 9. Повторяем теорию:Какие векторы называются перпендикулярными?Что называется скалярным
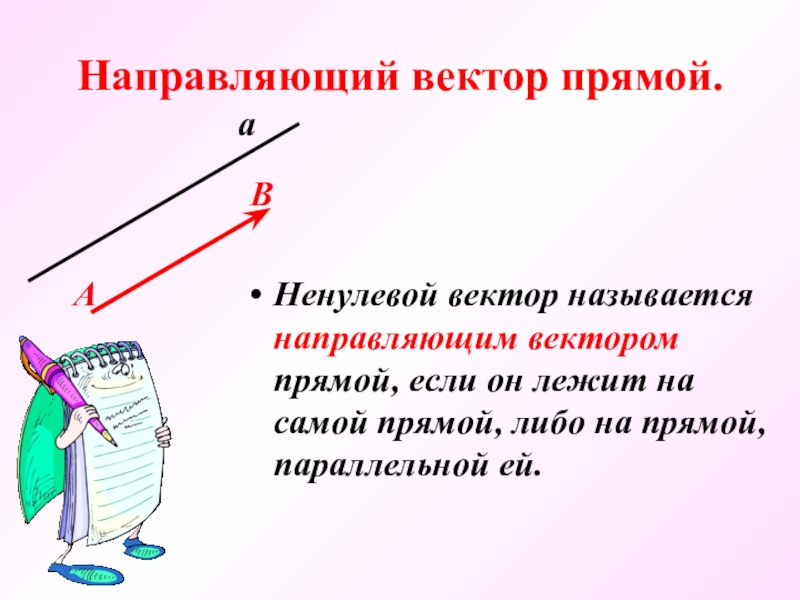
- 10. Направляющий вектор прямой.Ненулевой вектор называется направляющим вектором
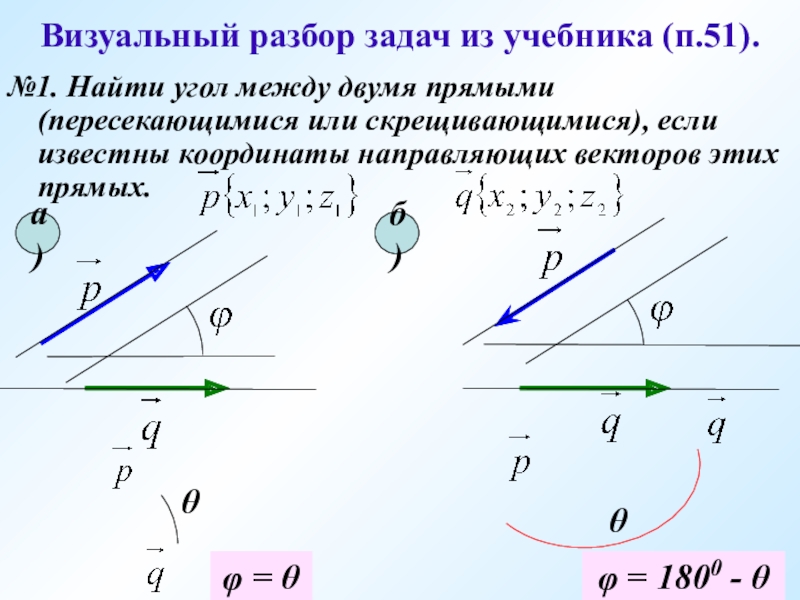
- 11. Визуальный разбор задач из учебника (п.51). №1.
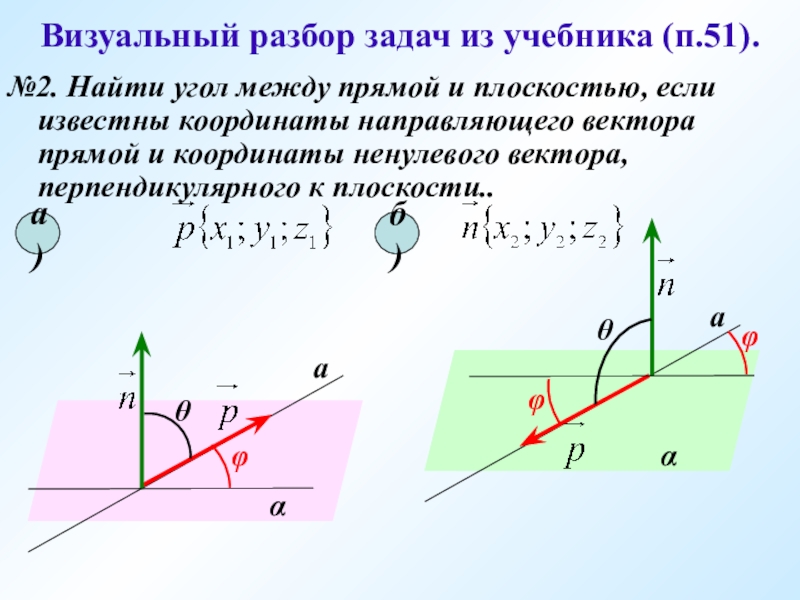
- 12. Визуальный разбор задач из учебника (п.51). №2.
- 13. № 464 (а)Дано:Найти: угол между прямыми АВ и CD.Ваши предложения…Найдем координаты векторови2. Воспользуемся формулой:φ = 300
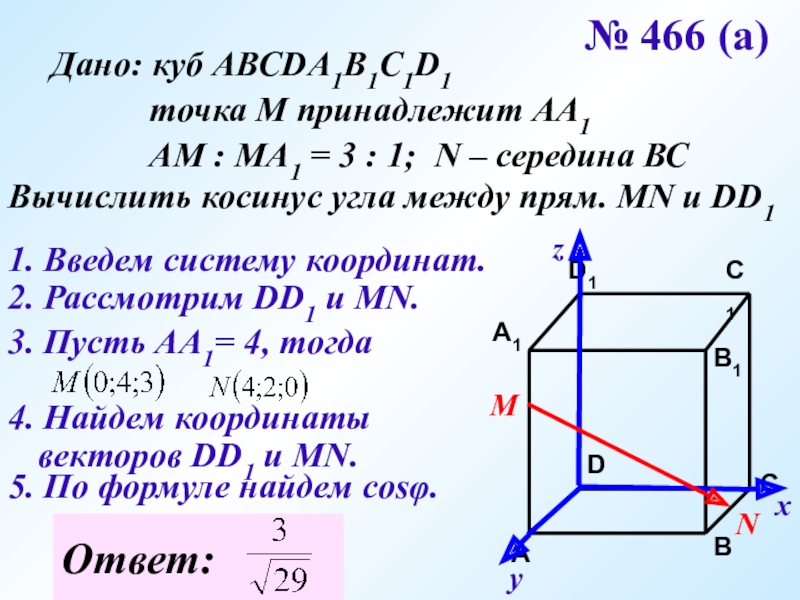
- 14. № 466 (а)Дано: куб АВСDA1B1C1D1
- 15. Задача.Дано: прямоугольный параллелепипед АВСDA1B1C1D1; DA = 2;
- 16. № 467 (а)Дано: прямоугольный параллелепипед
- 17. хуz№ 467 (а)Дано: прямоугольный параллелепипед
- 18. п. 52,№464 (б, в, г)№466 (б, в)Домашнее задание:
- 19. Слайд 19
Слайд 3Цели урока:
Показать, как используется скалярное произведение векторов при решении
Слайд 8Повторяем теорию:
Как находят координаты вектора, если известны координаты его начала и
Как находят координаты середины отрезка?
Как находят длину вектора?
Как находят расстояние между точками?
Как вы понимаете выражение «угол между векторами»?
Слайд 9Повторяем теорию:
Какие векторы называются перпендикулярными?
Что называется скалярным произведением векторов?
Чему равно скалярное
Чему равен скалярный квадрат вектора?
Свойства скалярного произведения?
0
Скалярный квадрат вектора равен квадрату его длины.
Слайд 10Направляющий вектор прямой.
Ненулевой вектор называется направляющим вектором прямой, если он лежит
а
В
А
Слайд 11Визуальный разбор задач из учебника (п.51).
№1. Найти угол между двумя
а)
б)
θ
θ
φ = θ
φ = 1800 - θ
Слайд 12Визуальный разбор задач из учебника (п.51).
№2. Найти угол между прямой
а)
б)
α
а
φ
θ
α
а
φ
φ
θ
Слайд 13№ 464 (а)
Дано:
Найти: угол между прямыми АВ и CD.
Ваши предложения…
Найдем координаты
и
2. Воспользуемся формулой:
φ = 300
Слайд 14№ 466 (а)
Дано: куб АВСDA1B1C1D1
АМ : МА1 = 3 : 1; N – середина ВС
Вычислить косинус угла между прям. MN и DD1
1. Введем систему координат.
х
у
z
2. Рассмотрим DD1 и МN.
М
N
3. Пусть АА1= 4, тогда
4. Найдем координаты векторов DD1 и MN.
5. По формуле найдем cosφ.
Ответ:
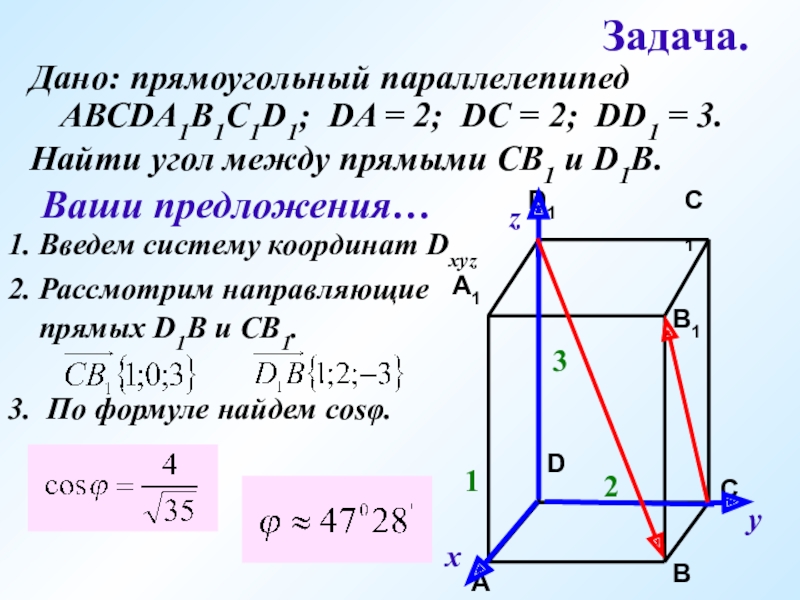
Слайд 15Задача.
Дано: прямоугольный параллелепипед АВСDA1B1C1D1; DA = 2; DC = 2; DD1
1
2
3
Найти угол между прямыми СВ1 и D1B.
х
у
z
Ваши предложения…
1. Введем систему координат Dxyz
2. Рассмотрим направляющие
прямых D1B и CB1.
3. По формуле найдем cosφ.
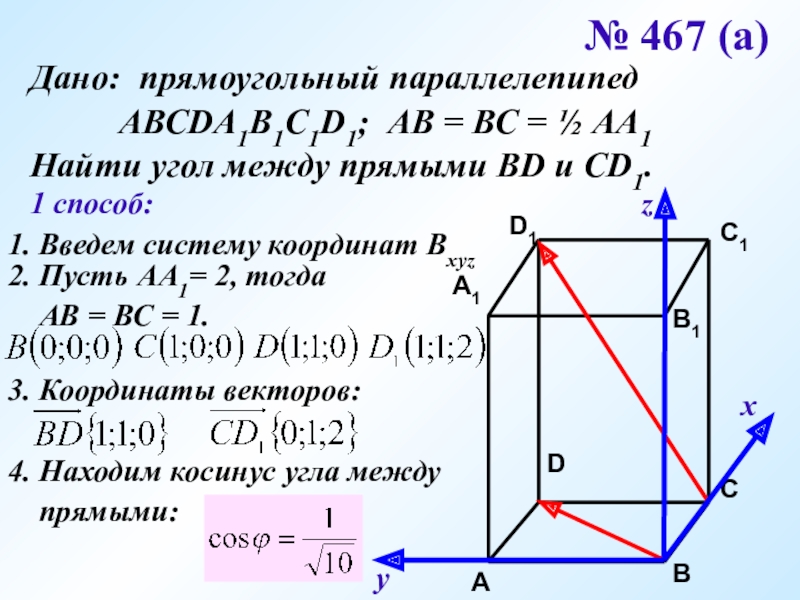
Слайд 16№ 467 (а)
Дано: прямоугольный параллелепипед
Найти угол между прямыми ВD и CD1.
1 способ:
1. Введем систему координат Bxyz
х
у
z
2. Пусть АА1= 2, тогда
АВ = ВС = 1.
3. Координаты векторов:
4. Находим косинус угла между
прямыми:
Слайд 17
х
у
z
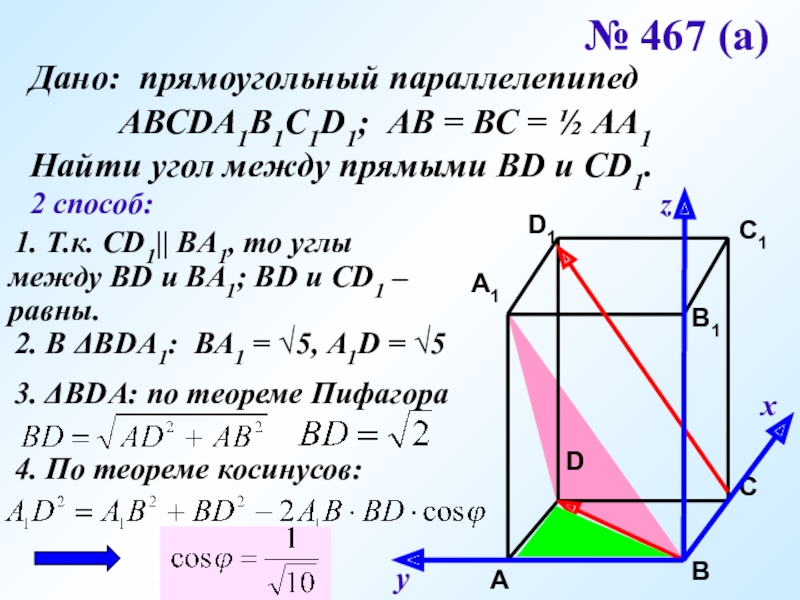
№ 467 (а)
Дано: прямоугольный параллелепипед
Найти угол между прямыми ВD и CD1.
2 способ:
1. Т.к. СD1|| ВА1, то углы между ВD и ВА1; ВD и СD1 – равны.
2. В ΔВDА1: ВА1 = √5, А1D = √5
3. ΔВDА: по теореме Пифагора
4. По теореме косинусов: