- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Вычисление площадей фигур
Содержание
- 1. Презентация по геометрии на тему Вычисление площадей фигур
- 2. Данная презентация, на примере различных методов, поможет
- 3. Понятие площади Площадь- численная характеристика двумерной геометрической
- 4. «Геометрия является самым могущественным средством для изощрения
- 5. Немного историиСуществует простая формула, по которой можно
- 6. Формула ПикаГеорг Алекса́ндр Пик (10.08.1859-13.07.1942) , австрийский математик.
- 7. Теорема Пика для вычисление площади многоугольника с
- 8. Мы будем пользоваться этой в более удобном
- 9. Пример 1. Найдите площадь четырехугольника, изображенного на
- 10. Пример 2. Найдите площадь четырехугольника, изображенного на
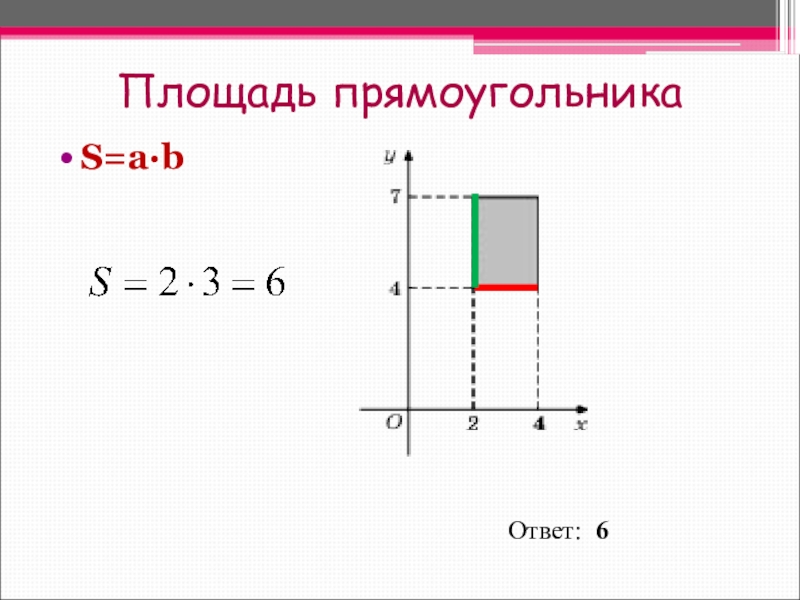
- 11. Площадь прямоугольникаS=a∙bОтвет: 6
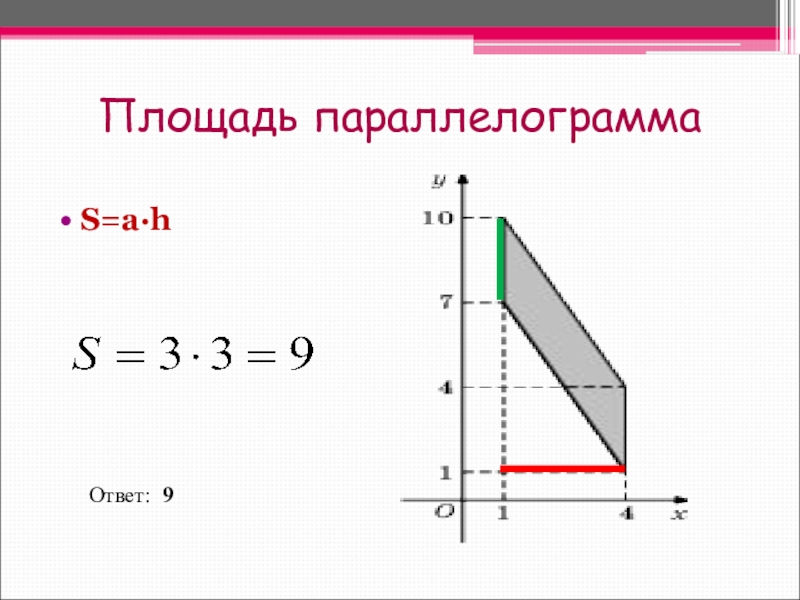
- 12. Площадь параллелограммаS=a∙hОтвет: 9
- 13. Площадь треугольникаS=a∙h/2
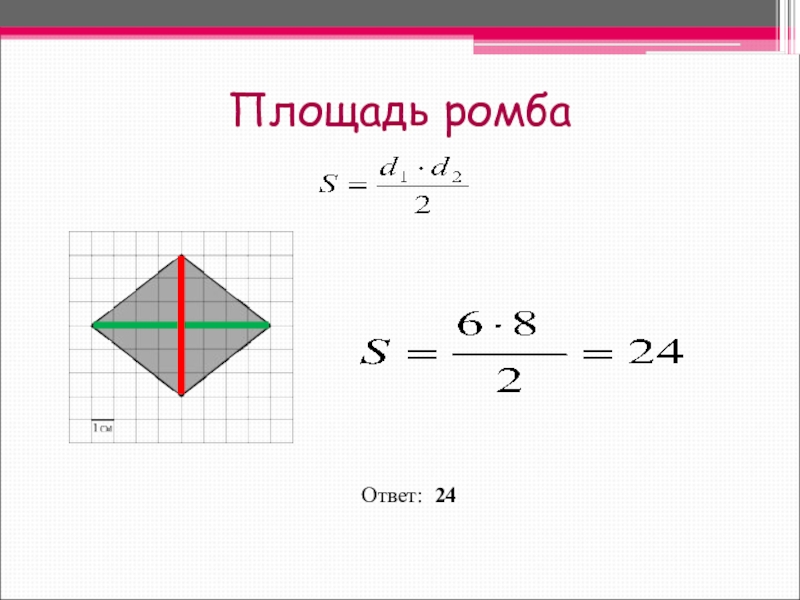
- 14. Площадь ромба Ответ: 24
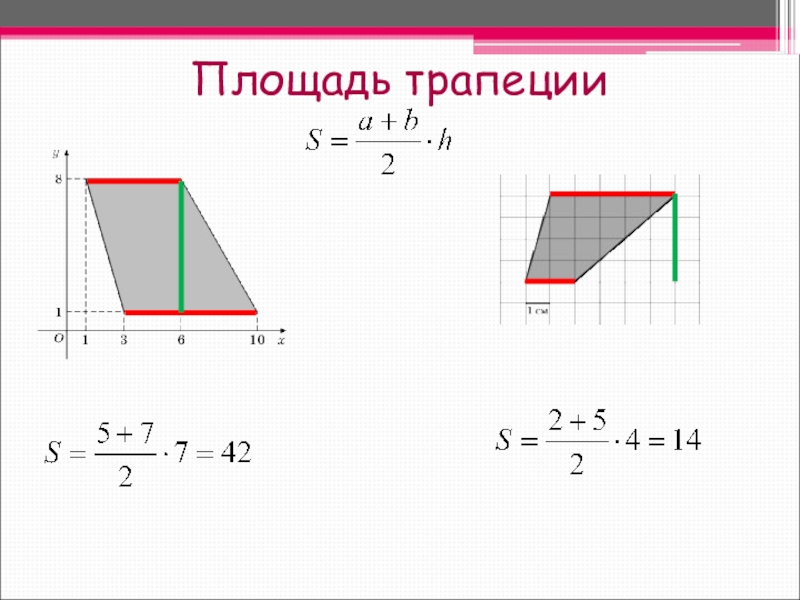
- 15. Площадь трапеции
- 16. Площадь кольцаНайдите площадь кольца, ограниченного концентрическими окружностями,
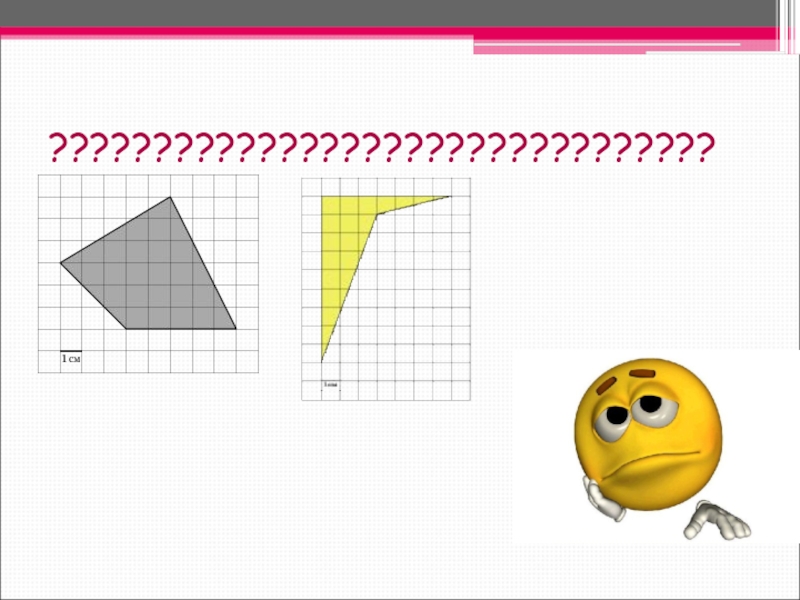
- 17. ????????????????????????????????
- 18. Дополнительное построениеОтвет: 27
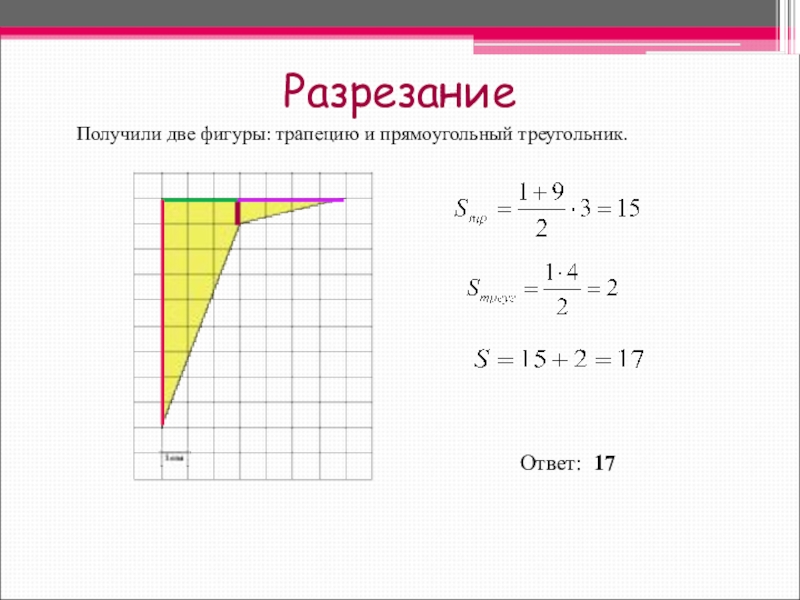
- 19. РазрезаниеПолучили две фигуры: трапецию и прямоугольный треугольник.Ответ: 17
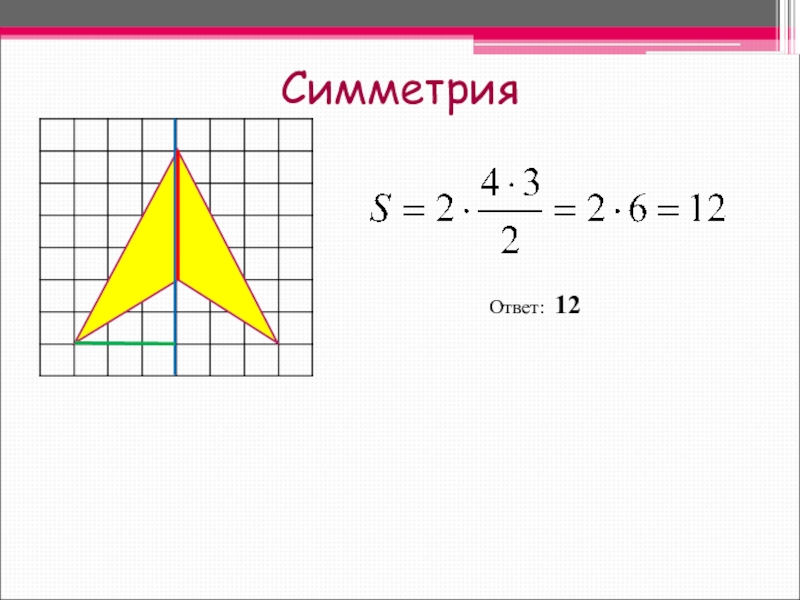
- 20. СимметрияОтвет: 12
- 21. Применение подобия
- 22. Итоги занятияПри решении задач на нахождение площадей
Данная презентация, на примере различных методов, поможет ученикам вычислять площади фигур как старыми способами, так и новым.
Слайд 1Методы вычисления площадей фигур.
Автор: Чистопольский Александр, ученик 9В класса
Руководитель: Мелешкина
Светлана Юрьевна
Слайд 2Данная презентация, на примере различных методов, поможет ученикам вычислять площади фигур
как старыми способами, так и новым.
Слайд 3Понятие площади
Площадь- численная характеристика двумерной геометрической фигуры, показывающая размер этой фигуры.
Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой.
Слайд 4«Геометрия является самым могущественным средством для изощрения умственных способностей и дает
нам возможность правильно мыслить и рассуждать».
Галилео Галилей.
«Глядя на мир, нельзя не удивляться»
Козьма Прутков
Слайд 5Немного истории
Существует простая формула, по которой можно легко вычислять площади многоугольников
с вершинами в узлах квадратной сетки.
Эту формулу открыл австрийский математик Пик Георг Александров (1859 – 1943 г.г.) в 1899 году. Кроме этой формулы Георг Пик открыл теоремы Пика, Пика – Жюлиа, Пика – Невалины, доказал неравенство Шварца – Пика.
Эту формулу открыл австрийский математик Пик Георг Александров (1859 – 1943 г.г.) в 1899 году. Кроме этой формулы Георг Пик открыл теоремы Пика, Пика – Жюлиа, Пика – Невалины, доказал неравенство Шварца – Пика.
Слайд 7
Теорема Пика для вычисление площади многоугольника с целочисленными вершинами .
Пусть L —
число целочисленных точек внутри многоугольника,
B— количество целочисленных точек на его границе,
S— его площадь.
Тогда справедлива формула Пика:
S=L+B/2-1
B— количество целочисленных точек на его границе,
S— его площадь.
Тогда справедлива формула Пика:
S=L+B/2-1
Слайд 8
Мы будем пользоваться этой в более удобном для нас виде. Введём
другие обозначения:
В - число целочисленных точек внутри многоугольника,
Г - количество целочисленных точек на его границе, тогда формула Пика будет иметь вид:
S=В+Г/2-1
В - число целочисленных точек внутри многоугольника,
Г - количество целочисленных точек на его границе, тогда формула Пика будет иметь вид:
S=В+Г/2-1
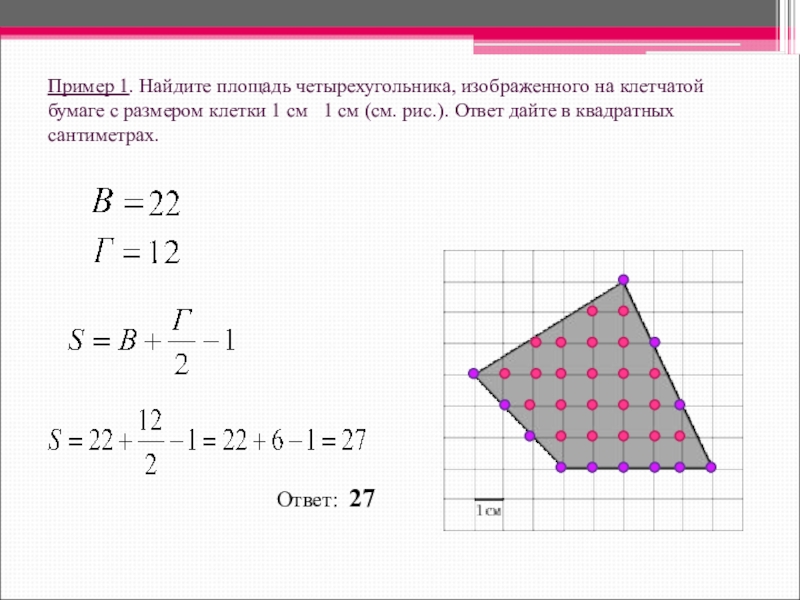
Слайд 9Пример 1. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером
клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ: 27
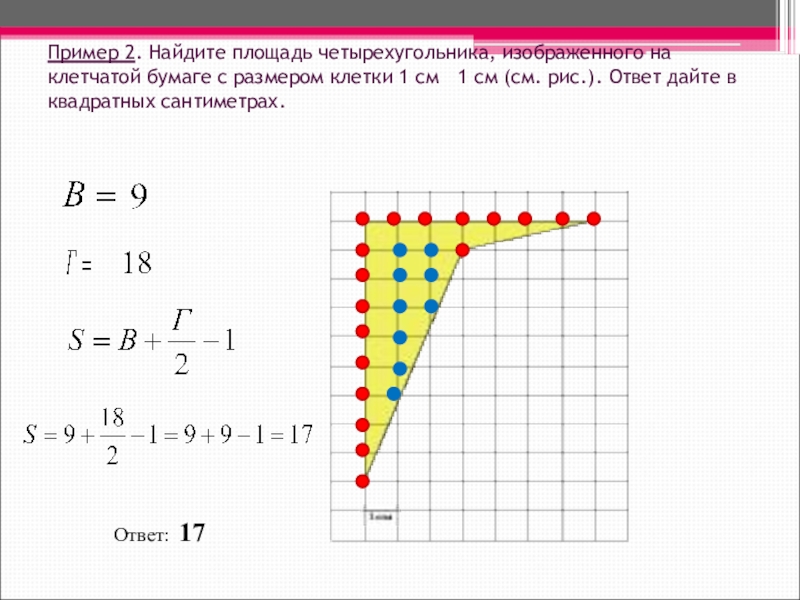
Слайд 10Пример 2. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером
клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ: 17
Слайд 16Площадь кольца
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны
.
Ответ: 104
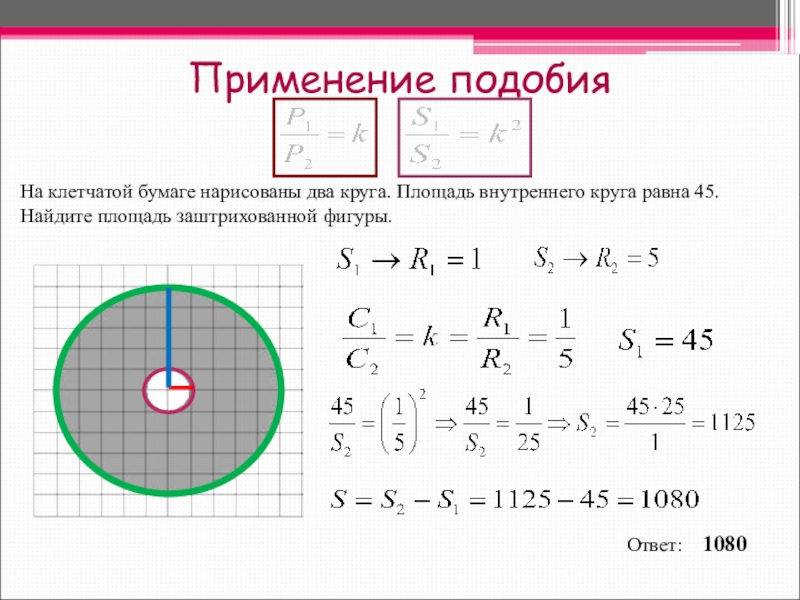
Слайд 21Применение подобия
На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 45. Найдите площадь заштрихованной фигуры.
Ответ: 1080
Слайд 22Итоги занятия
При решении задач на нахождение площадей фигур можно использовать следующие
методы:
1. Основные формулы вычисления площадей плоских фигур.
2. Метод дополнительного построения .
3. Метод разрезания.
4. Формула Пика.
5. Применение подобия.
6. Осевая симметрия.
1. Основные формулы вычисления площадей плоских фигур.
2. Метод дополнительного построения .
3. Метод разрезания.
4. Формула Пика.
5. Применение подобия.
6. Осевая симметрия.