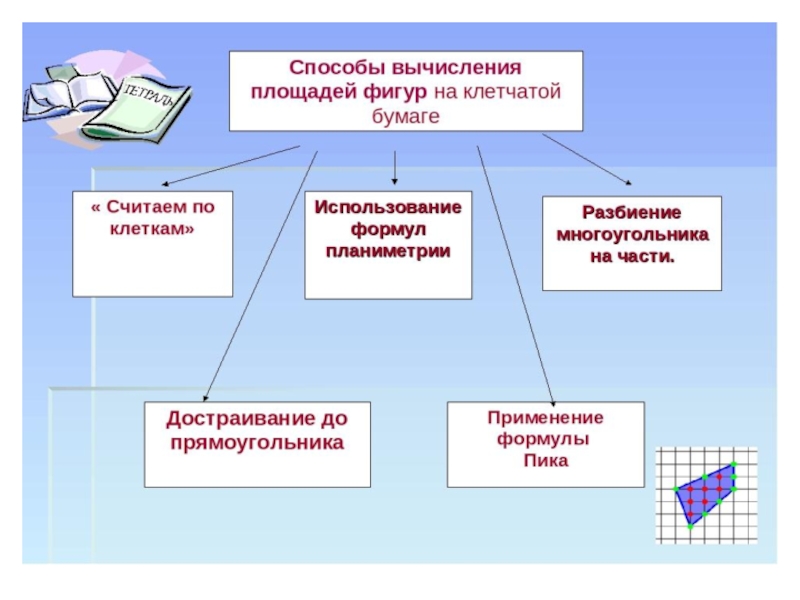
Презентация, доклад по геометрии на тему: Вычисление площади многоугольников на клетчатой бумаге

Полуполтинных Дмитрий
Руководитель:
Яновская Светлана Ивановна
г. Находка
2019

по формулам, если фигура представляет собой треугольник, параллелограмм или трапецию.
3.Второй способ: метод разбиения.
4.Третий способ: метод дополнительного построения.
5.Четвёртый способ: Формула Пика.
6.Практическая часть: опрос (анкетирование).
7. Заключение.
8. Используемая литература.

по ОГЭ я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатой бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой треугольник, параллелограмм или трапецию. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приёмы. Меня заинтересовала эта тема. И естественно возник вопрос: существуют ли другие способы для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?
1.Актуальность:
Данная тема пригодится при решении заданий на ОГЭ и ЕГЭ
2.Объект исследования:
Фигуры на клетчатой бумаге
Предмет исследования:
Нахождение площади многоугольников на клетчатой бумаге

Введение

клетчатой бумаге
4.Задачи исследовательской работы:
Изучить литературу по исследуемой теме.
Отобрать интересную и понятную информацию для исследования.
Найти различные методы и приёмы вычисления площади многоугольников на клетчатой бумаге.
Проанализировать и систематизировать полученную информацию.
5.Методы исследовательской работы:
Моделирование, сравнение, обобщение, аналогии, анализ и классификация изученной информации.
 

1)

1.Площадь треугольника можно определить по формуле

1)

2.Площадь трапеции можно вычислить по формуле

прямоугольника

4. Площадь параллелограмма можно вычислить по формуле

S=2∙3=6

многоугольник разрезается на прямоугольники или прямоугольные треугольники с вершинами в узлах сетки, а затем вычислить площади полученных фигур и найти сумму всех площадей.

1.Разделим четырёхугольник на четыре прямоугольных треугольника

2.Найдём площадь первого треугольника

3.Найдём площадь второго треугольника

4.Найдём площадь третьего треугольника

5.Найдём площадь четвертого треугольника

6.Найдём площадь четырёхугольника

Ответ: 12,5.

S=4+1+3+4,5=12,5

четырехугольника. Получили квадрат со стороной 5

 

Третий способ – дополнение до прямоугольника

Смысл данного способа – это дополнение многоугольника до прямоугольника, а затем найти площади полученных дополнительных фигур и площадь самого прямоугольника и из площади прямоугольника вычесть площади всех лишних частей.

2.Найдём площадь квадрата

3.Найдём площадь первого треугольника

4.Найдём площадь второго треугольника

5.Найдём площадь третьего треугольника

6.Найдём площадь четвертого треугольника

7. Найдём площадь четырёхугольника

Ответ: 12,5

(10 августа 1859 — 13 июля 1942) — австрийский математик, родился в еврейской семье. Круг математических интересов Пика был чрезвычайно широк. Им написаны работы в области математического анализа, дифференциальной геометрии, в теории дифференциальных уравнений и т. д., всего более 50 тем. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. Сто лет назад австрийский математик Георг Пик обнаружил замечательную формулу для вычисления площади многоугольника с вершинами в узлах клетчатой бумаги.

Пусть у многоугольника, изображённого на клетчатой бумаге только целочисленные вершины. Точки у которых обе координаты целые называются узлами решетки. Причем, многоугольник может быть как выпуклым, так и невыпуклым. Площадь многоугольника с целочисленными вершинами равна S = B + Г/2 – 1, где B – количество целочисленных точек внутри многоугольника, а Г – количество целочисленных точек на границе многоугольника.

количество узлов, лежащих внутри - B =10

Вычисляем площадь четырёхугольника

S=7/2+10-1=12,5.

Ответ: 12,5

№ 2

решению задач на клетчатой бумаге и нахождению площадей фигур и убедился в многообразии способов вычисления площади многоугольника. Кроме рассмотренных мною в данной работе 4 способов существуют и другие. Исследуемый мною вопрос достаточно интересен, полезен, но очень объёмен. Задачи на клетчатой бумаге встречаются в заданиях ЕГЭ и ОГЭ, поэтому следует хорошо знать ни один способ вычисления площади многоугольника. Цели и задачи, поставленные в начале работы, были выполнены. Хочу отметить, что любой из рассмотренных мною способов применим для решения задач.
 

Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.