- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Введение Теоремы Пифагора (8 класс)
Содержание
- 1. Презентация по геометрии на тему Введение Теоремы Пифагора (8 класс)
- 2. Цели:Образовательные: познакомить учащихся с теоремой Пифагора, а
- 3. ТЕСТТреугольник называется прямоугольным, если у него один
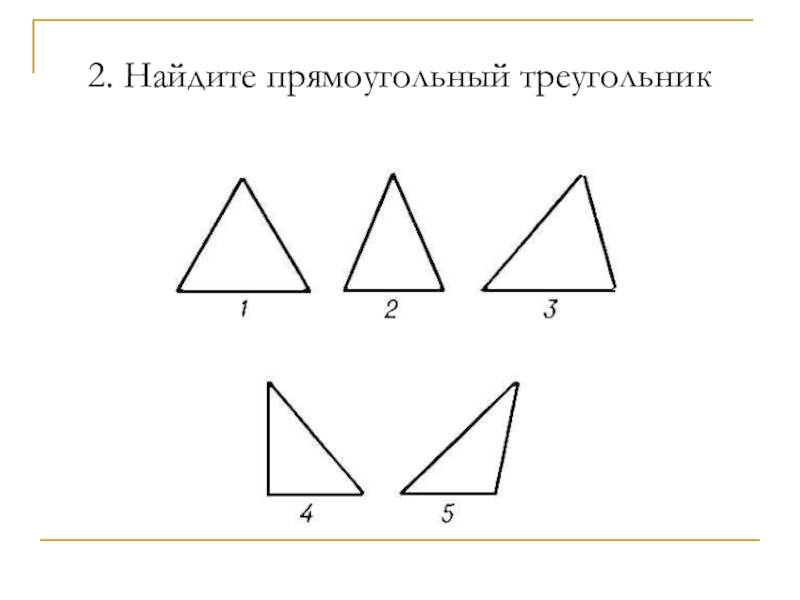
- 4. 2. Найдите прямоугольный треугольник
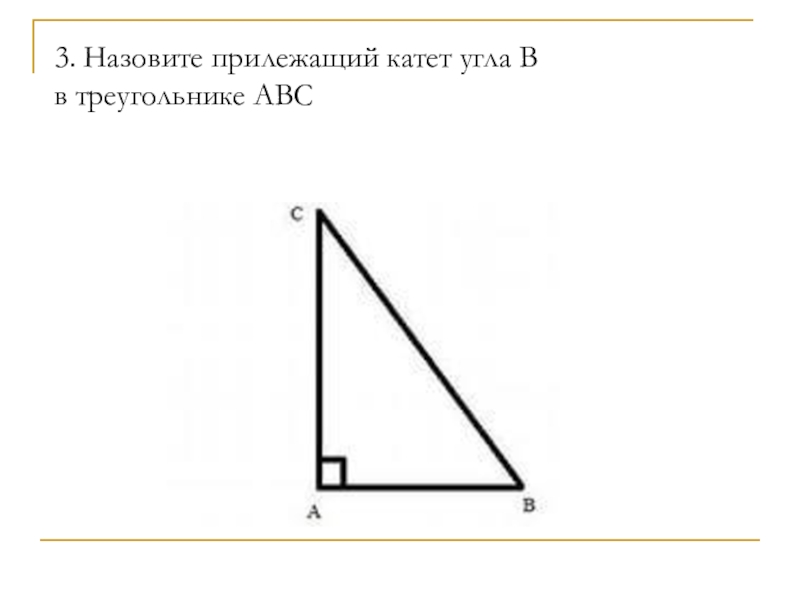
- 5. 3. Назовите прилежащий катет угла B в треугольнике ABC
- 6. 4. Чем является сторона АВ в треугольнике
- 7. 6. Какая сторона прямоугольного треугольника называется гипотенузой?7. Какие стороны прямоугольного треугольника называются катетами?
- 8. 8. С помощью, каких формул можно найти площадь квадрата и площадь треугольника?
- 9. СКАЗКА "Давным - давно в
- 10. …ведьма придумала усыпить принцессу в башне до
- 11. И вот принцесса заснула крепким
- 12. В один прекрасный
- 13. Для этого он измеряет длину
- 14. Мультфильм
- 15. Пифагор Самосский - знаменитый греческий математик, механик,
- 16. Акусмумы ПифагораБерегите слёзы ваших детей, дабы они
- 17. Теорема Пифагора в древности звучала так:
- 18. «Пифагоровы штаны на все стороны равны»
- 19. Теорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
- 20. «Приключения Электроника»
- 21. Доказательство теоремы Пифагора 1.
- 22. Доказательство теоремы Пифагора 2.
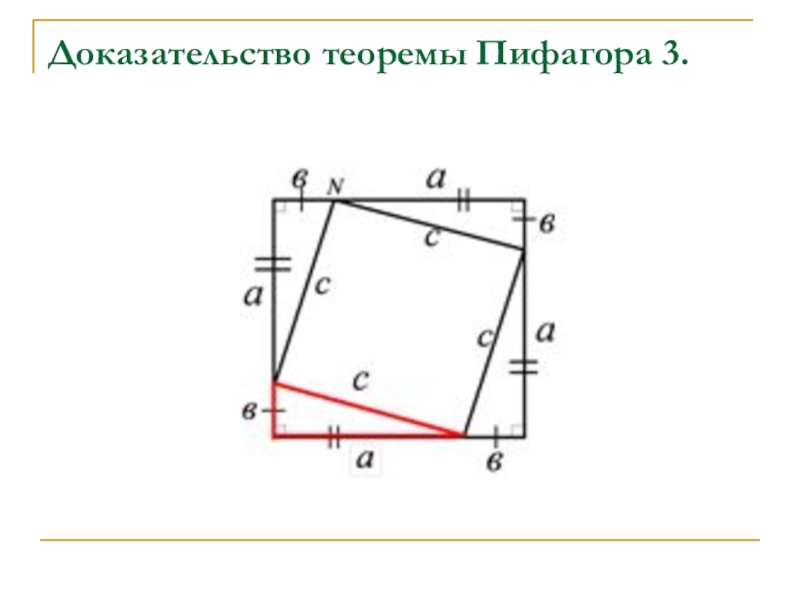
- 23. Доказательство теоремы Пифагора 3.
- 24. Алгоритм решения задач по теореме ПифагораВнимательно прочитай
- 25. Признак
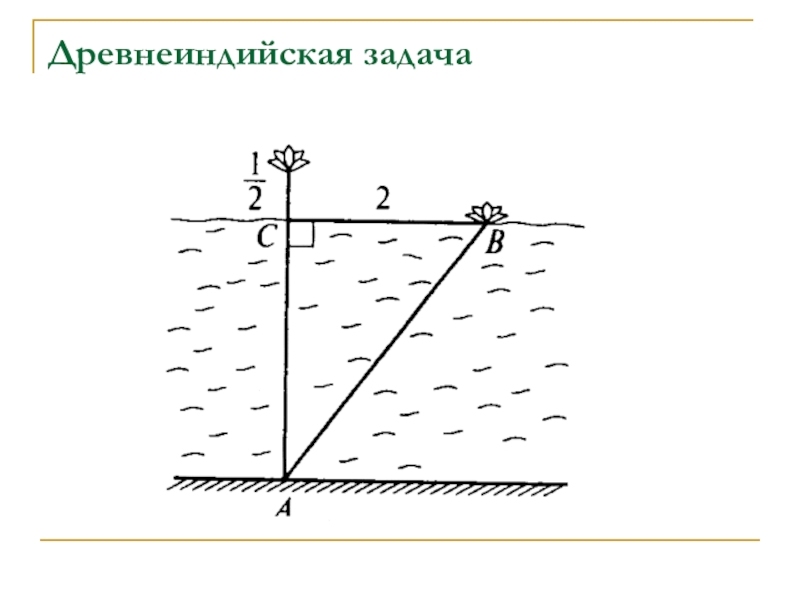
- 26. Древнеиндийская задача Над озером тихим С
- 27. Древнеиндийская задача
- 28. Ералаш
Цели:Образовательные: познакомить учащихся с теоремой Пифагора, а также с многообразием способов ее доказательства;Воспитательные: воспитывать познавательную активность, повышать интерес к изучению математики, применяя ИКТ. Развивающие: развивать умения доказывать новые математические утверждения, развивать мышление, память, навыки аргументированной речи.Методы
Слайд 2Цели:
Образовательные: познакомить учащихся с теоремой Пифагора, а также с многообразием способов
ее доказательства;
Воспитательные: воспитывать познавательную активность, повышать интерес к изучению математики, применяя ИКТ.
Развивающие: развивать умения доказывать новые математические утверждения, развивать мышление, память, навыки аргументированной речи.
Методы обучения: частично-поисковый, объяснительно-иллюстративный
Средства обучения: компьютер, мультимедийный проектор.
Структура урока:
Организационный момент. (2 мин)
Актуализация опорных знаний.(7 мин)
Объяснение нового материала. (15 мин)
Различные способы доказательства теоремы Пифагора.(10 мин)
Решение задачи (7 мин)
Постановка домашнего задания. Подведение итогов.(4 мин)
Воспитательные: воспитывать познавательную активность, повышать интерес к изучению математики, применяя ИКТ.
Развивающие: развивать умения доказывать новые математические утверждения, развивать мышление, память, навыки аргументированной речи.
Методы обучения: частично-поисковый, объяснительно-иллюстративный
Средства обучения: компьютер, мультимедийный проектор.
Структура урока:
Организационный момент. (2 мин)
Актуализация опорных знаний.(7 мин)
Объяснение нового материала. (15 мин)
Различные способы доказательства теоремы Пифагора.(10 мин)
Решение задачи (7 мин)
Постановка домашнего задания. Подведение итогов.(4 мин)
Слайд 3ТЕСТ
Треугольник называется прямоугольным, если у него один из углов:
а) 45°
в) 60°
б) 180° г) 90°
б) 180° г) 90°
Слайд 64. Чем является сторона АВ в треугольнике ABC?
5. Чем являются стороны
АС и ВС в треугольнике ABC?
Слайд 76. Какая сторона прямоугольного треугольника называется гипотенузой?
7. Какие стороны прямоугольного треугольника
называются катетами?
Слайд 9СКАЗКА
"Давным - давно в некоторой стране жила прекрасная
принцесса и была она настолько прекрасной, что затмевала красотой всех своих подруг и свою старшую сестру, которая красотой не блистала. Старшая сестра завидовала принцессе и решила ей отомстить. Тогда она пошла к ведьме и попросила её заколдовать принцессу. Ведьма не смогла ей отказать, но все же, ей стало жалко принцессу, поэтому…
Слайд 10
…ведьма придумала усыпить принцессу в башне до той поры, пока какой
- нибудь принц не посмотрит на окно башни с такого места, чтобы расстояние от глаз принца до окна было 50 шагов.
Слайд 11 И вот принцесса заснула крепким сном. Прошло много лет,
но никто не смог расколдовать принцессу, несмотря на то, что Король (отец ее) пообещал отдать принцессу в жены тому, кто спасет её от пут сна.
Слайд 12 В один прекрасный день в этом городе
появляется на белом прекрасном коне молодой принц. Узнав, какое несчастье произошло с принцессой, молодой принц берется расколдовать её.
Слайд 13
Для этого он измеряет длину от основания башни до
окна, за которым скрывается принцесса. У него получается 30 шагов. Затем что - то прикидывает в уме и отходит на 40 шагов, поднимает голову и вдруг. . . башня озаряется светом и через мгновенье навстречу принцу выбегает еще более прекрасная принцесса. . ."
Слайд 15Пифагор Самосский - знаменитый греческий математик, механик, музыкант, философ, геометр, олимпийский
чемпион древности.
Родился в 500г до нашей эры и прожил 80 лет.
Родился в 500г до нашей эры и прожил 80 лет.
Слайд 16Акусмумы Пифагора
Берегите слёзы ваших детей, дабы они могли проливать их на
вашей могиле.
Во время гнева не должно ни говорить, ни действовать.
Живи с людьми так, чтобы твои друзья не стали недругами, а недруги стали друзьями.
Молчание прекрасно. Молчи, если не можешь изречь то, что было бы прекрасней молчания.
Просыпаясь утром, спроси себя: «Что я должен сделать?», а, засыпая вечером, спроси: «Что я сделал?»
Во время гнева не должно ни говорить, ни действовать.
Живи с людьми так, чтобы твои друзья не стали недругами, а недруги стали друзьями.
Молчание прекрасно. Молчи, если не можешь изречь то, что было бы прекрасней молчания.
Просыпаясь утром, спроси себя: «Что я должен сделать?», а, засыпая вечером, спроси: «Что я сделал?»
Слайд 17Теорема Пифагора в древности
звучала так:
Площадь квадрата, построенного на
гипотенузе прямоугольного
треугольника,
равна сумме площадей квадратов
построенных на его катетах.
равна сумме площадей квадратов
построенных на его катетах.
Слайд 19Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 24Алгоритм решения задач по теореме Пифагора
Внимательно прочитай условие задачи
Сделай чертёж
Выдели на
чертеже прямоугольный треугольник
Найди катеты и гипотенузу
Запиши теорему Пифагора и соотнеси данные в задаче с ней
Выполни подстановку данных
Соотнеси полученный ответ с вопросом задачи и смыслом условия
Радуйся тому, что задача решена верно!
Найди катеты и гипотенузу
Запиши теорему Пифагора и соотнеси данные в задаче с ней
Выполни подстановку данных
Соотнеси полученный ответ с вопросом задачи и смыслом условия
Радуйся тому, что задача решена верно!
Слайд 26Древнеиндийская задача
Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос
одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”