- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Виды симметрий на плоскости
Содержание
- 1. Презентация по геометрии на тему Виды симметрий на плоскости
- 2. Проектная работа по геометрииРуководитель Парфенова Светлана Михайловна
- 3. Что такое симметрия?Симме́три́я (др.-греч. συμμετρία = «соразмерность»;
- 4. Симметрия в геометрииГеометрическая симметрия — это наиболее
- 5. Зеркальная симметрияЗеркальная симметрия или отражение — движение
- 6. Осевая симметрияФигура называется симметричной относительно прямой А,
- 7. Вращательная симметрияВращательная симметрия — термин, означающий симметрию
Проектная работа по геометрииРуководитель Парфенова Светлана Михайловна
Слайд 3Что такое симметрия?
Симме́три́я (др.-греч. συμμετρία = «соразмерность»; от συμ- «совместно» +
μετρέω «мерю»), в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях (например: положения, энергии, информации, другого). Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.
Слайд 4Симметрия в геометрии
Геометрическая симметрия — это наиболее известный тип симметрии для
многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг повёрнутый вокруг своего центра будет иметь ту же форму и размер, что и исходный круг. Поэтому круг называется симметричным относительно вращения (имеет осевую симметрию). Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования.
Слайд 5Зеркальная симметрия
Зеркальная симметрия или отражение — движение евклидова пространства, множество неподвижных
точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью). Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, то есть, когда объект при операции отражения переходит в себя. Это математическое понятие в оптике описывает соотношение объектов и их (мнимых) изображений при отражении в плоском зеркале. Проявляется во многих законах природы (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении).
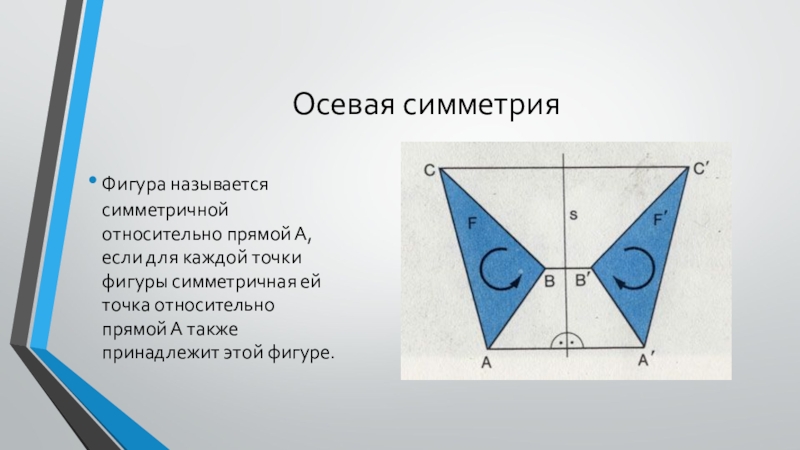
Слайд 6Осевая симметрия
Фигура называется симметричной относительно прямой А, если для каждой точки
фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.
Слайд 7Вращательная симметрия
Вращательная симметрия — термин, означающий симметрию объекта относительно всех или
некоторых собственных вращений m-мерного евклидова пространства. Собственными вращениями называются разновидности изометрии, сохраняющие ориентацию. Таким образом, группа симметрии, отвечающая вращениям, есть подгруппа группы E+(m) (см. Евклидова группа).
Трансляционная симметрия может рассматриваться как частный случай вращательной — вращение вокруг бесконечно-удалённой точки. При таком обобщении группа вращательной симметрии совпадает с полной E+(m). Такого рода симметрия неприменима к конечным объектам, поскольку делает всё пространство однородным, однако она используется в формулировке физических закономерностей.
Трансляционная симметрия может рассматриваться как частный случай вращательной — вращение вокруг бесконечно-удалённой точки. При таком обобщении группа вращательной симметрии совпадает с полной E+(m). Такого рода симметрия неприменима к конечным объектам, поскольку делает всё пространство однородным, однако она используется в формулировке физических закономерностей.