- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Виды многогранников
Содержание
- 1. Презентация по геометрии на тему Виды многогранников
- 2. Понятие многогранника Куб, шар, пирамида,
- 3. Виды многогранников Различают выпуклые и
- 4. Грани, вершины, и ребра
- 5. Основные виды многогранников:1. Обычные или классические:пирамидапризма2. Правильные многогранники (также называемые Платоновыми телами)
- 6. Общие свойства многогранников : Все
- 7. Правильные многогранники Если
- 8. В
- 9. Школа Пифагора Одной из самых
- 10. Вопрос 1 Какую форму, по мнению
- 11. Вопрос 2Какую форму, по мнению пифагорейцев, имела вся Вселенная?
- 12. Упражнение 1Сколько граней (Г) имеет:Ответ: Г =
- 13. Упражнение 2Сколько вершин (В) имеет:Ответ: В =
- 14. Упражнение 3Сколько ребер (Р) имеет:Ответ: Р =
- 15. Призма Основания – это две грани,
- 16. Боковая поверхность призмы – объединение боковых граней.Полная
- 17. Пирамида Пирамида — это многогранник,
- 18. Обозначая пирамиду, сначала называют
Слайд 2Понятие многогранника
Куб, шар, пирамида, цилиндр, конус — геометрические
Многогранником называют геометрическое тело, поверхность которого состоит из конечного числа многоугольников.
Каждый из этих многоугольников называется гранью многогранника,
стороны и вершины этих многоугольников — соответственно ребрами и вершинами многогранника.
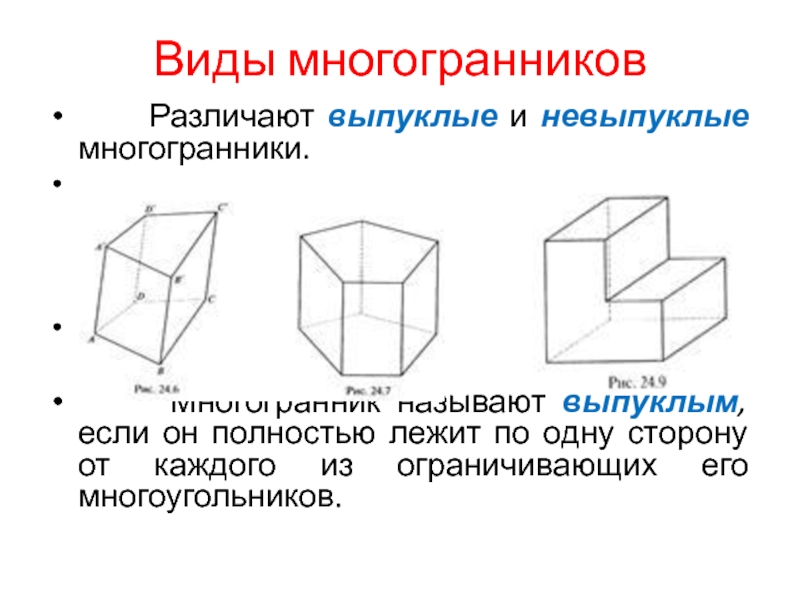
Слайд 3Виды многогранников
Различают выпуклые и невыпуклые многогранники.
Многогранник называют выпуклым, если он полностью лежит по одну сторону от каждого из ограничивающих его многоугольников.
Слайд 4 Грани, вершины, и ребра многогранников связаны между собой
Г+В-Р=2,
где: Г - число граней, В - число вершин и Р - число ребер.
Число граней многогранника не может быть меньше четырех,
а сумма углов многоугольников, сходящихся в одной вершине, многогранных углов, не должно быть больше 2.
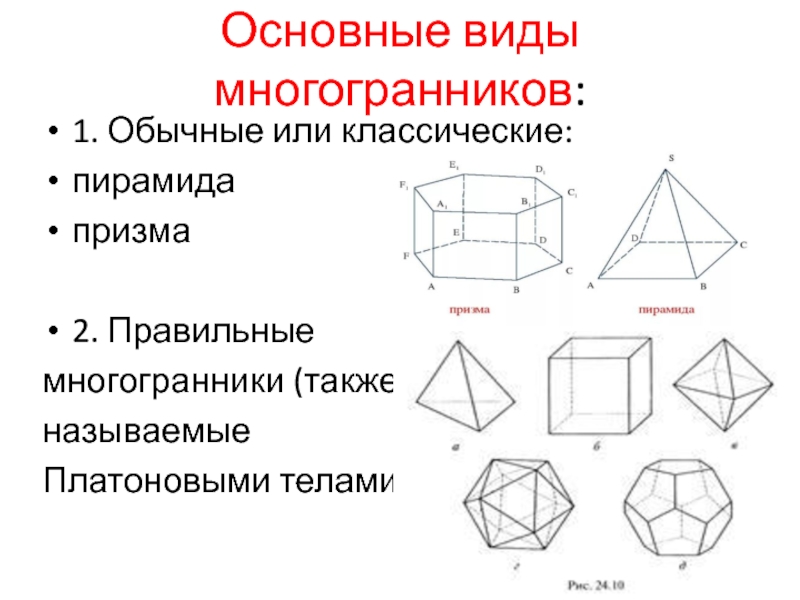
Слайд 5Основные виды многогранников:
1. Обычные или классические:
пирамида
призма
2. Правильные
многогранники (также
называемые
Платоновыми
Слайд 6Общие свойства многогранников :
Все они имеют 3 неотъемлемых
грань (поверхность многоугольника),
вершина (углы, образовавшиеся в местах соединения граней),
ребро (сторона фигуры или отрезок, образованный в месте стыка двух граней).
Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению друг к другу являются смежными.
Слайд 7Правильные многогранники
Если в каждой вершине многогранника
Если в каждой вершине многогранника сходится четыре правильных треугольника, то получаем октаэдр (окто – восемь) (рис. 3). Его поверхность состоит из восьми правильных треугольников.
Если в каждой вершине многогранника сходится пять правильных треугольников, то получаем икосаэдр(икоси–двадцать)(рис. 4). Его поверхность состоит из двадцати правильных треугольников.
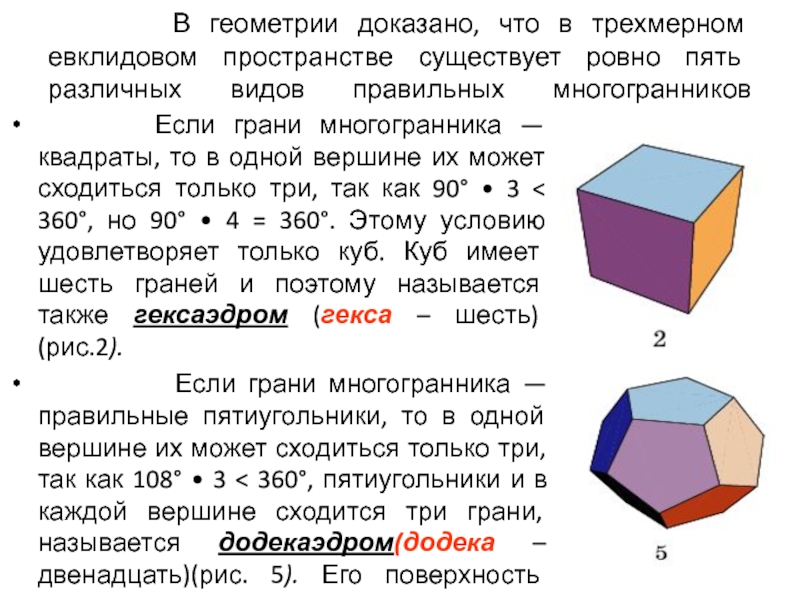
Слайд 8 В геометрии доказано, что в трехмерном евклидовом
Если грани многогранника — квадраты, то в одной вершине их может сходиться только три, так как 90° • 3 < 360°, но 90° • 4 = 360°. Этому условию удовлетворяет только куб. Куб имеет шесть граней и поэтому называется также гексаэдром (гекса – шесть) (рис.2).
Если грани многогранника — правильные пятиугольники, то в одной вершине их может сходиться только три, так как 108° • 3 < 360°, пятиугольники и в каждой вершине сходится три грани, называется додекаэдром(додека – двенадцать)(рис. 5). Его поверхность состоит из двенадцати правильных пятиугольников.
Слайд 9Школа Пифагора
Одной из самых первых и самых известных
Объяснение устройства мира пифагорейцы тесно связывали с геометрией. Так, выделяя первоосновы бытия, они приписывали их атомам форму правильных многогранников, а именно: атомам огня - форму тетраэдра (рис. 1), земли – гексаэдра (куба, рис. 2), воздуха – октаэдра (рис. 3), воды – икосаэдра (рис. 4). Всей Вселенной приписывалась форма додекаэдра (рис. 5).
Слайд 10
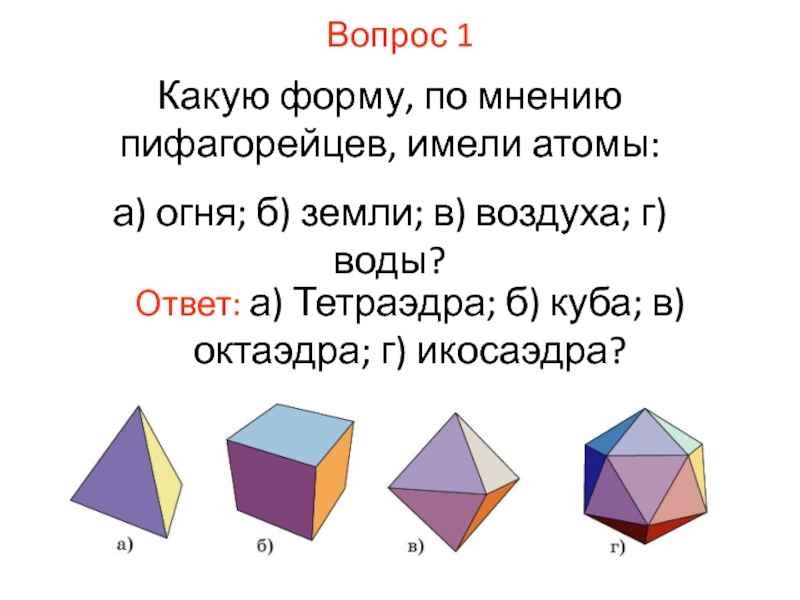
Вопрос 1
Какую форму, по мнению пифагорейцев, имели атомы:
а) огня; б)
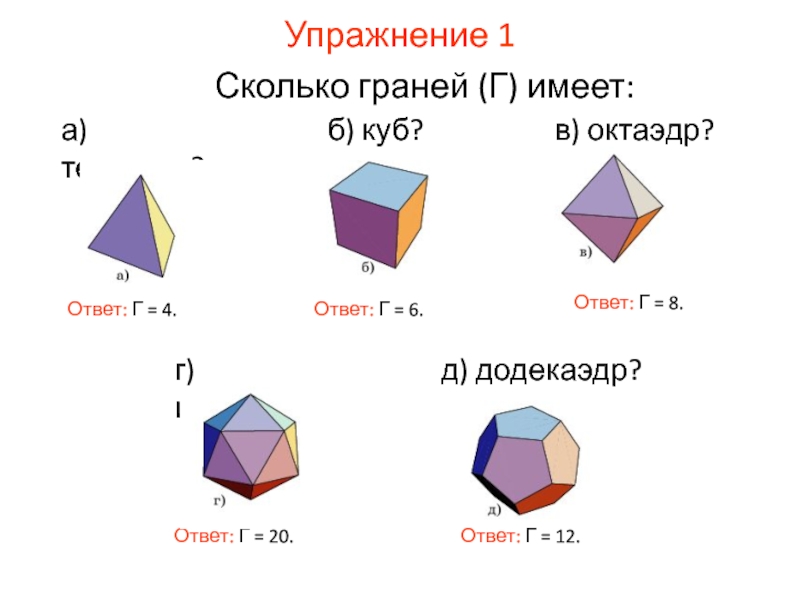
Слайд 12Упражнение 1
Сколько граней (Г) имеет:
Ответ: Г = 4.
Ответ: Г = 6.
Ответ:
Ответ: Г = 20.
Ответ: Г = 12.
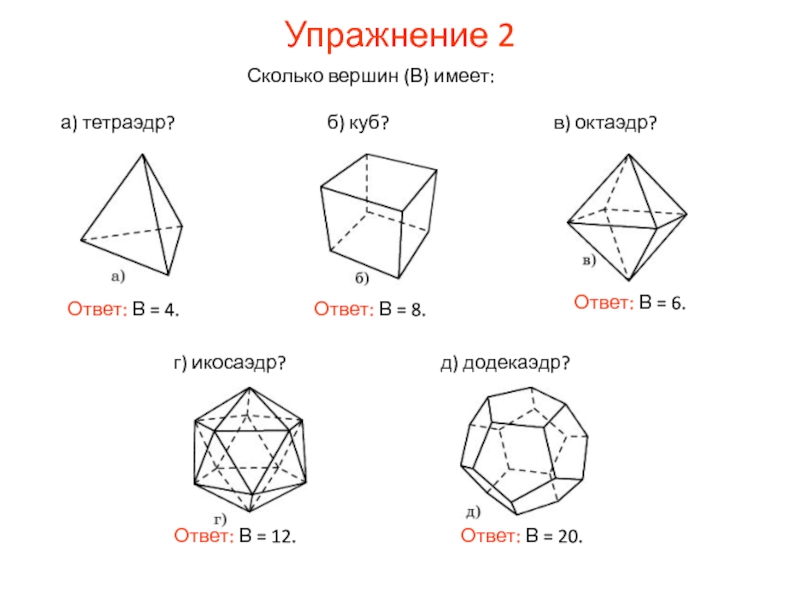
Слайд 13Упражнение 2
Сколько вершин (В) имеет:
Ответ: В = 8.
Ответ: В = 6.
Ответ:
Ответ: В = 20.
Ответ: В = 4.
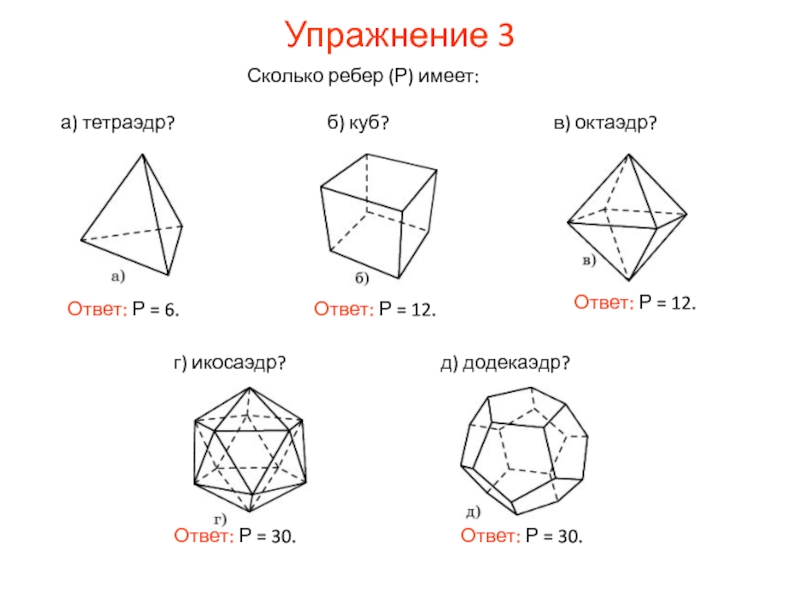
Слайд 14Упражнение 3
Сколько ребер (Р) имеет:
Ответ: Р = 12.
Ответ: Р = 12.
Ответ:
Ответ: Р = 30.
Ответ: Р = 6.
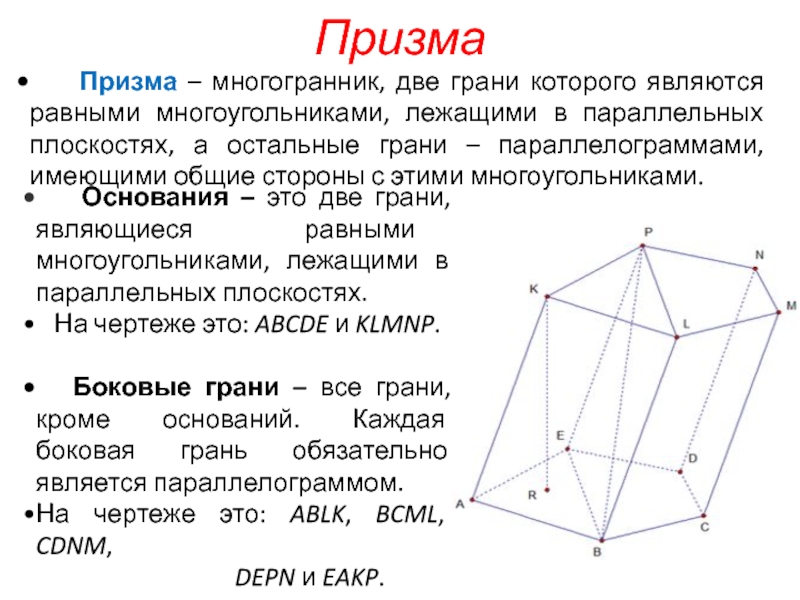
Слайд 15Призма
Основания – это две грани, являющиеся равными многоугольниками, лежащими
На чертеже это: ABCDE и KLMNP.
Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом.
На чертеже это: ABLK, BCML, CDNM,
DEPN и EAKP.
Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
Слайд 16Боковая поверхность призмы – объединение боковых граней.
Полная поверхность призмы – объединение
Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
Слайд 17Пирамида
Пирамида — это многогранник, поверхность которого состоит из
Общая вершина этих треугольников называется вершиной пирамиды, ребра, выходящие из вершины, — боковыми ребрами пирамиды.
Перпендикуляр, опущенный из вершины пирамиды на основание, а также длина этого перпендикуляра называется высотой пирамиды.
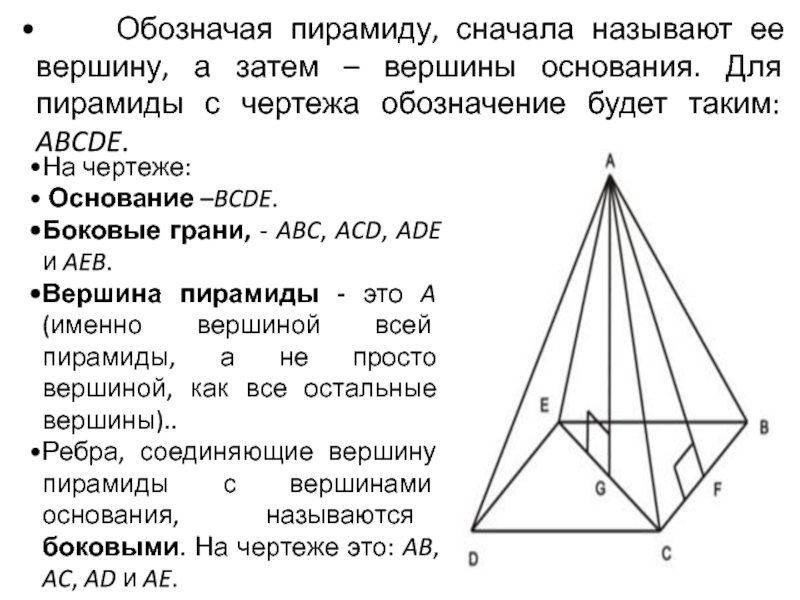
Слайд 18 Обозначая пирамиду, сначала называют ее вершину, а затем
На чертеже:
Основание –BCDE.
Боковые грани, - ABC, ACD, ADE и AEB.
Вершина пирамиды - это A (именно вершиной всей пирамиды, а не просто вершиной, как все остальные вершины)..
Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми. На чертеже это: AB, AC, AD и AE.