- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Векторы (9 класс)
Содержание
- 1. Презентация по геометрии на тему Векторы (9 класс)
- 2. Вектор – направленный отрезокДлина ненулевого вектора – длина соответствующего отрезкаВекторыКоллинеарныеНеколлинеарныеПротивоположно направленныеСонаправленные
- 3. Равные векторы - это1) сонаправленные векторы, которые2)
- 4. Сложение векторовОпределение: суммой двух векторов называют результат их последовательного откладывания.
- 5. Сложение векторовПравило треугольника: суммой векторов, отложенных
- 6. Сложение векторовПравило параллелограмма: если векторы отложены
- 7. Свойства сложенияa + b = b +
- 8. Противоположные векторыОпределение: векторы a и b
- 9. Вычитание векторовОпределение: разностью двух векторов a
- 10. Вычитание векторовПравило треугольника: чтобы из вектора
- 11. Вычитание векторовПравило параллелограмма: Если векторы отложены
- 12. Две задачиЗадача о середине отрезка: Вектор,
Вектор – направленный отрезокДлина ненулевого вектора – длина соответствующего отрезкаВекторыКоллинеарныеНеколлинеарныеПротивоположно направленныеСонаправленные
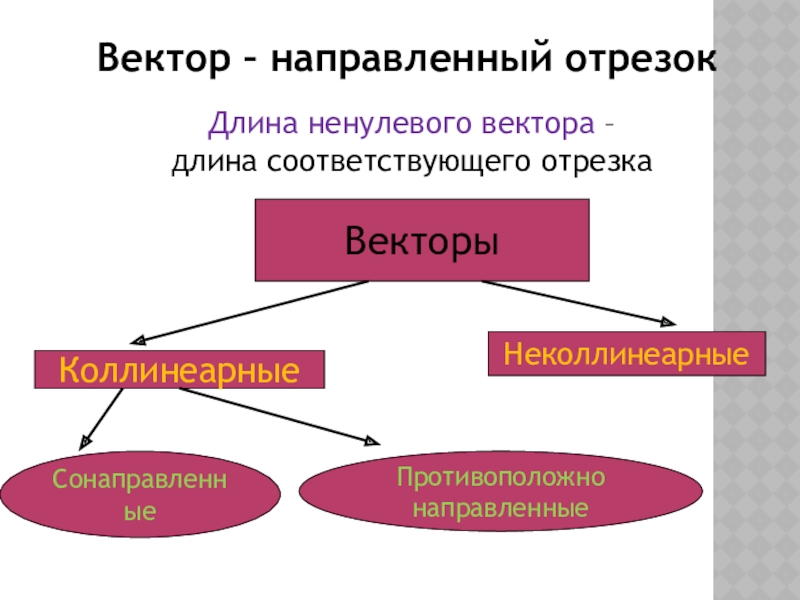
Слайд 2Вектор – направленный отрезок
Длина ненулевого вектора –
длина соответствующего отрезка
Векторы
Коллинеарные
Неколлинеарные
Противоположно направленные
Сонаправленные
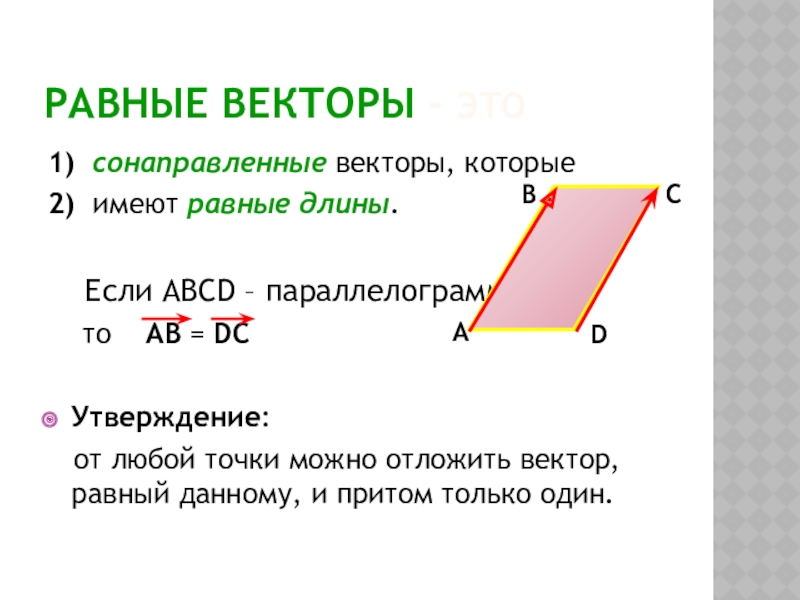
Слайд 3Равные векторы - это
1) сонаправленные векторы, которые
2) имеют равные длины.
Если ABCD – параллелограмм,
то AB = DC
Утверждение:
от любой точки можно отложить вектор, равный данному, и притом только один.
А
В
С
D
Слайд 4Сложение векторов
Определение:
суммой двух векторов
называют
результат их последовательного откладывания.
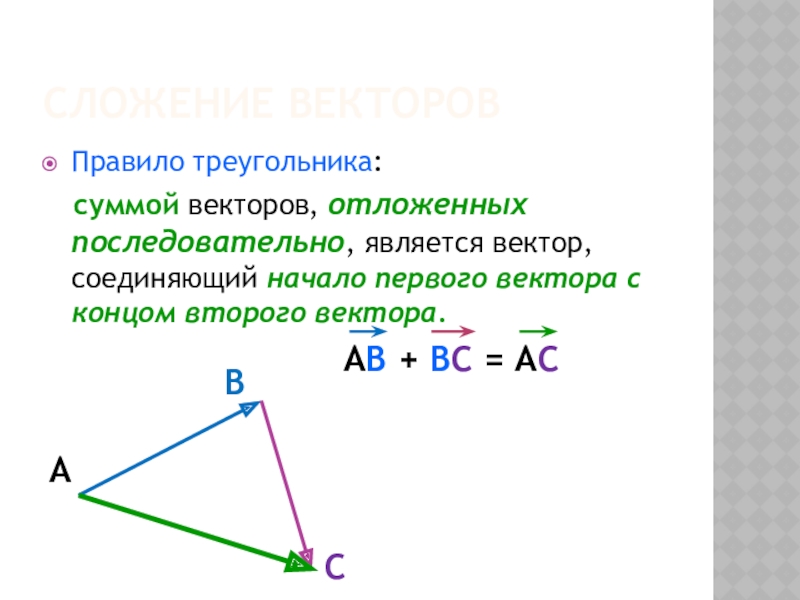
Слайд 5Сложение векторов
Правило треугольника:
суммой векторов, отложенных последовательно, является вектор, соединяющий
начало первого вектора с концом второго вектора.
АВ + ВС = АС
АВ + ВС = АС
А
В
С
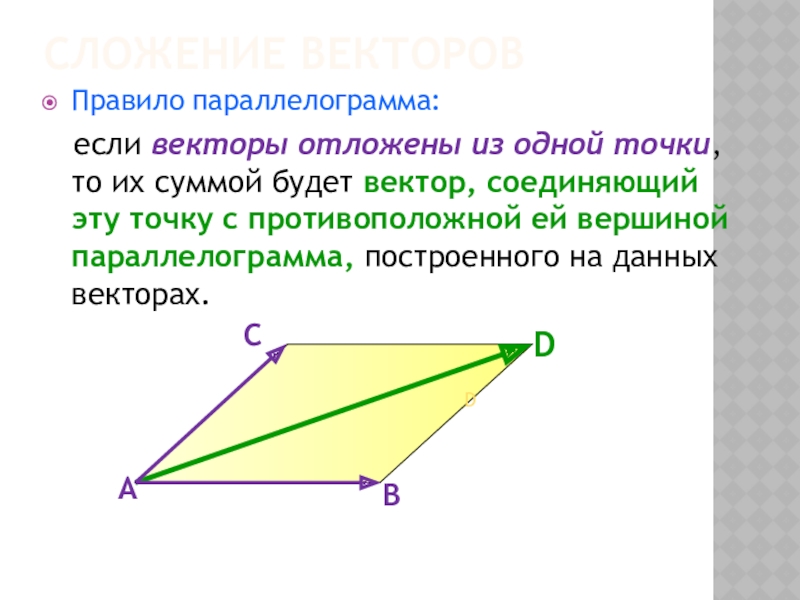
Слайд 6Сложение векторов
Правило параллелограмма:
если векторы отложены из одной точки, то
их суммой будет вектор, соединяющий эту точку с противоположной ей вершиной параллелограмма, построенного на данных векторах.
А
В
С
D
D
Слайд 7Свойства сложения
a + b = b + a
(переместительный закон)
(a + b)
+ c = a + (b + c)
(сочетательный закон)
(сочетательный закон)
Слайд 8Противоположные векторы
Определение:
векторы a и b называются противоположными, если
1) они – противоположно направленные векторы и
2) их длины равны.
Обозначение: a = -b ( b = -a)
AB = -CD
CD = -AB
2) их длины равны.
Обозначение: a = -b ( b = -a)
AB = -CD
CD = -AB
A
B
C
D
Слайд 9Вычитание векторов
Определение:
разностью двух векторов a и b называют
такой вектор c,
сумма которого с вектором b равна вектору a.
a – b = c, если c + b = a
сумма которого с вектором b равна вектору a.
a – b = c, если c + b = a
Слайд 10Вычитание векторов
Правило треугольника:
чтобы из вектора a вычесть вектор b,
надо к вектору a прибавить вектор, противоположный вектору b.
a – b = a + (-b)
(в этом случае векторы a и -b откладываются друг за другом)
a – b = a + (-b)
(в этом случае векторы a и -b откладываются друг за другом)
a
-b
a - b
a
b
Слайд 11Вычитание векторов
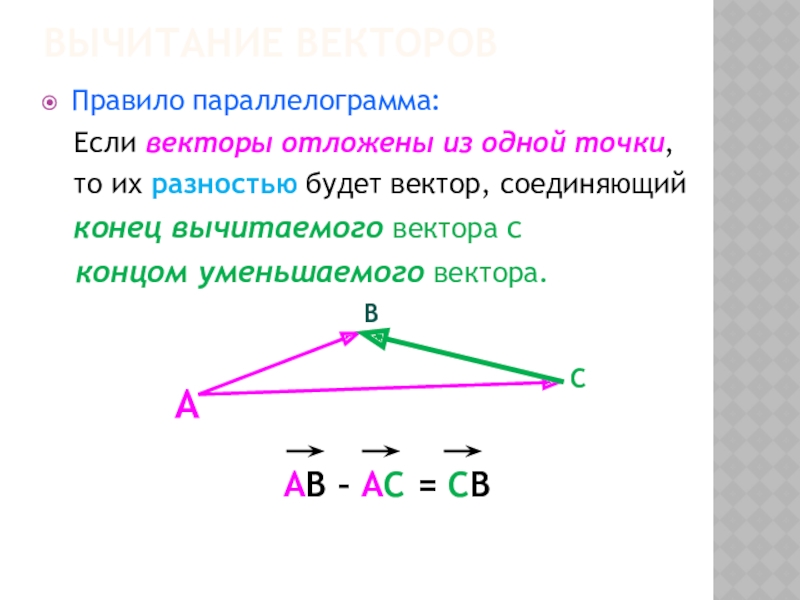
Правило параллелограмма:
Если векторы отложены из одной точки,
то их разностью будет вектор, соединяющий
конец вычитаемого вектора с
концом уменьшаемого вектора.
AB – AC = CВ
конец вычитаемого вектора с
концом уменьшаемого вектора.
AB – AC = CВ
A
B
C
Слайд 12Две задачи
Задача о середине отрезка:
Вектор, соединяющий произвольную точку пространства
с серединой отрезка, равен полусумме векторов, соединяющих эту точку с концами данного отрезка.
Задача о точке пересечения медиан треугольника:
Вектор, соединяющий произвольную точку пространства с точкой пересечения медиан треугольника, равен одной трети суммы векторов, соединяющих эту точку с вершинами данного треугольника.
Задача о точке пересечения медиан треугольника:
Вектор, соединяющий произвольную точку пространства с точкой пересечения медиан треугольника, равен одной трети суммы векторов, соединяющих эту точку с вершинами данного треугольника.