на каждой из них обозначается направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Векторы в пространстве (11 класс)
Содержание
- 1. Презентация по геометрии на тему Векторы в пространстве (11 класс)
- 2. Плоскости, проходящие соответственно через оси координат Ох
- 3. Положительная полуось – Отрицательная полуось -Луч, направление которого совпадает с направлением осиДругой луч
- 4. КООРДИНАТЫ ВЕКТОРАВ пространстве зададим прямоугольную систему координат
- 5. Правила нахождения координат вектора:1. каждая координата суммы
- 6. ПрактикаНайти координаты вектора p = 2a -
- 7. Координаты вектора, радиус-вектора и точкиКоординаты вектора
- 8. Найдите длину вектора а, b если
- 9. Нахождение середины отрезкаА (5;8;3)B (2;6;0)C – середина
- 10. 1) d + a2) d{-2,7;3,1;0,5}
- 11. Дано: ОА = 4, ОВ = 9,
- 12. Спасибо за внимание)
Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох и обозначаются Оху, Оуz, ОzxОси координат -Начало координат -O xyz-Координатные плоскости -прямые с выбранными на них направлениямиобщая точка осей координат.обозначение всей
Слайд 1Векторы в пространстве
Если через точку пространства проведены три попарно перпендикулярные прямые,
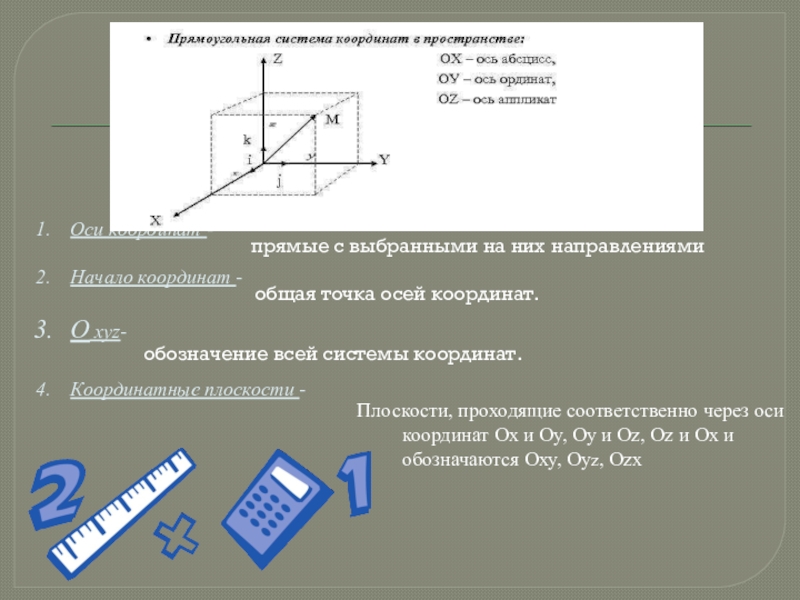
Слайд 2Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и
Оz, Оz и Ох и обозначаются Оху, Оуz, Оzx
Оси координат -
Начало координат -
O xyz-
Координатные плоскости -
прямые с выбранными на них направлениями
общая точка осей координат.
обозначение всей системы координат.
Слайд 3Положительная полуось –
Отрицательная полуось -
Луч, направление которого совпадает с направлением
оси
Другой луч
Слайд 4КООРДИНАТЫ ВЕКТОРА
В пространстве зададим прямоугольную систему координат Oxyz. От начала координат
в положительных направлениях осей Ox, Oy, Oz проведем соответствующие единичные векторы i , j , k , которые называются координатными векторами. Поэтому любой вектор a разлагается по трем заданным некомпланарным координатным векторам i , j и k с единственными коэффициентами разложения x, y, z:
a = x i + y j + z k
Тогда а {x;y;z}
Слайд 5Правила нахождения координат вектора:
1. каждая координата суммы двух или более векторов
равна сумме соответствующих координат заданных векторов. Если даны два вектора a {x1; y1; z1} и b {x2; y2; z2}, то сумма векторов a + b дает вектор с координатами {x1 + x2; y1 + y2; z1 + z2}
a + b {x1 + x2; y1 + y2; z1 + z2}
2. Разность соответствующих координат дает каждую координату вектора, полученного при вычитании двух заданных векторов. Если даны два вектора a {x1; y1; z1} и b {x2; y2; z2}, то разность векторов a - b дает вектор с координатами {x1 – x2; y1 – y2; z1 – z2}
a - b = {x1 – x2; y1 – y2; z1 – z2}
3. При умножении вектора на число каждая координата вектора равна произведению этого числа на соответствующую координату заданного вектора. Если даны число k и вектор a {x; y; z}, то умножение вектора на число k дает вектор k a с координатами
k a = {kx; ky; kz}
Слайд 6Практика
Найти координаты вектора p = 2a - 3b + 4c ,
если координаты векторов
a {1; -2; -1}, b {-2; 3; -4}, c {-1; -3; 2}
a {1; -2; -1}, b {-2; 3; -4}, c {-1; -3; 2}
Решение
p = 2 a - 3 b + 4 c
2 a =
{2·1; 2·(-2); 2·(-1)} =
{2; -4; -2}
3 b =
a {1; -2; -1}
b {-2; 3; -4}
{3·(-2); 3·3; 3·(-4} =
{-6; 9; -12}
c {-1; -3; 2}
4 c =
{4·(-1); 4·(-3); 4·2} =
{-4; -12; 8}
2) 2 a {2; -4; -2}
3 b {-6; 9; -12}
4 c {-4; -12; 8}
p =
{2 + 6 - 4; -4 - 9 -12; -2 + 12 + 8} =
{4; -25; 18}.
Слайд 7Координаты вектора,
радиус-вектора и точки
Координаты вектора –
Радиус-вектор –
это координаты конца вектора,
если начало вектора поместить в начало координат.
это вектор, проведенный из начала координат к данной точке, координаты радиус-вектора и точки равны.
а
А1 (х1;у1;z1)
А2 (х2;у2;z2)
A1(x1;y1;z1)
A2(x2;y2;z2)
a = A1A2{x2-x1;y2-y1;z2-z1}
Найдите координаты вектора МК, если
М(10;-4;2),К(16;2;-5)
ЗАДАЧА
Решение:
М(10;-4;2)
К (16;2;-5)
МК {16-10; 2-(-4); -5-2}
МК {6;6;-7}
Ответ:
МК{6;6;-7}
Слайд 8Найдите длину вектора а, b
если
а{5;0;6}, b{3,2;4;8}
|a| =
5
+ 0 + 6
2 2 2
|a| =
25+0+36
|a| =
61
1)
Длина вектора
|b| =
2)
|b| =
|b| =
10 + 4 + 8
100+16+64
200
2 2 2
Ответ:
61 ;
10
100*2
10
2
Слайд 9Нахождение середины отрезка
А (5;8;3)
B (2;6;0)
C – середина отрезка
Тогда С ( 5+2;8+6;3+0)
2
2
2
C(3,5;7;3)
A(-2;3;7)
B(3;14;0)
AB
=
(3-(-2)) + (14-3) + (0-7)
2 2 2
A(x1;y1;z1)
B(x2;y2;z2)
C- середина отрезка
C = —— ; —— ; ——
x1+x2 y1+y2 z1+z2
2 2 2
Задание
Нахождение расстояния между двумя точками
A(x1;y1;z1)
B(x2;y2;z2)
AB= (x2-x1) + (y2-y1) + (z2-z1)
2 2 2
Задание
AB =
25+121+49
AB =
195
Ответ: АВ= 195
Слайд 101) d + a
2) d{-2,7;3,1;0,5}
a{3;-5;2}
3) d+a{-2,7+3;3,1-5;0,5+2}
4) d+a{0,3;-1,9;2,5}
1
2
1) a
+ c
2) a{3;-5;2}
c{—;0;0}
3) a+с{3+—;-5+0;2+0}
4) a+с{3 —;-5;2}
2
3
2
3
2
3
3
1) b+c
2) b{0;7;-1}
c{—;0;0}
2
3
3) b+c{0+—;7+0;-1+0}
2
3
4) b+c{—;7;-1}
2
3
Ответ:
d+a{0,3;-1,9;2,5};
a+с{3 —;-5;2} ;
2
3
b+c{—;7;-1}
2
3
Слайд 11Дано:
ОА = 4, ОВ = 9, ОС = 2
А(4;0;0)
В(0;9;0)
С(0;0;2)
Найти:
Координаты АС,
СВ, АВ
Решение:
АС {0-4;0-0:2-0}
AC{-4;0;2}
3) А(4;0;0)
С(0;0;2)
2) В(0;9;0)
С(0;0;2)
BC{0-0;0-9;2-0}
BC{0;-9;2}
1)А(4;0;0)
В(0;9;0)
AB{0-4;9-0;0-0}
AB{-4;9;0}
Ответ: AB{-4;9;0}; BC{0;-9;2}; AC{-4;0;2}
Практика
