- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему В мире треугольников (7 класс)
Содержание
- 1. Презентация по геометрии на тему В мире треугольников (7 класс)
- 2. Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.
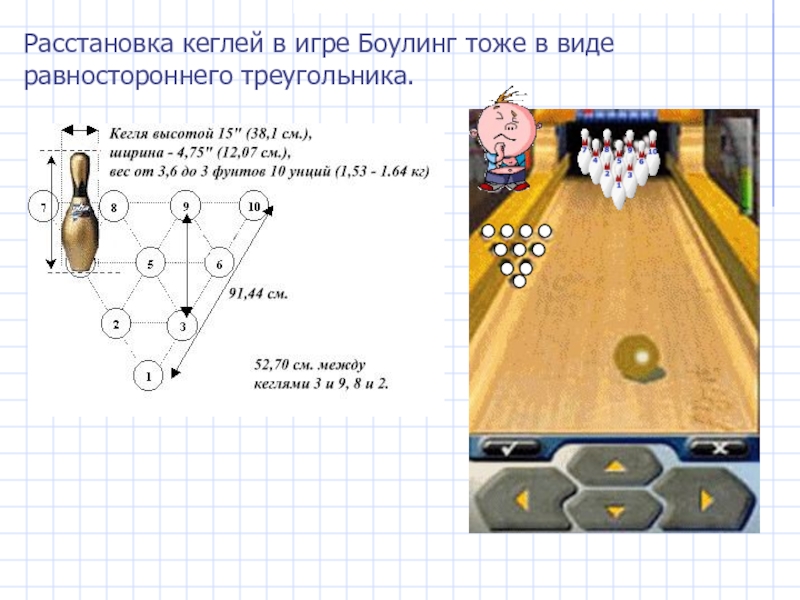
- 3. Расстановка кеглей в игре Боулинг тоже в виде равностороннего треугольника.
- 4. При расположении товара на прилавках супермаркета, обязательно учитывается правило «золотого треугольника», основанное на психологии покупателя.
- 5. В художественной литературе, телесериалах сюжет часто завязан на «любовном треугольнике».
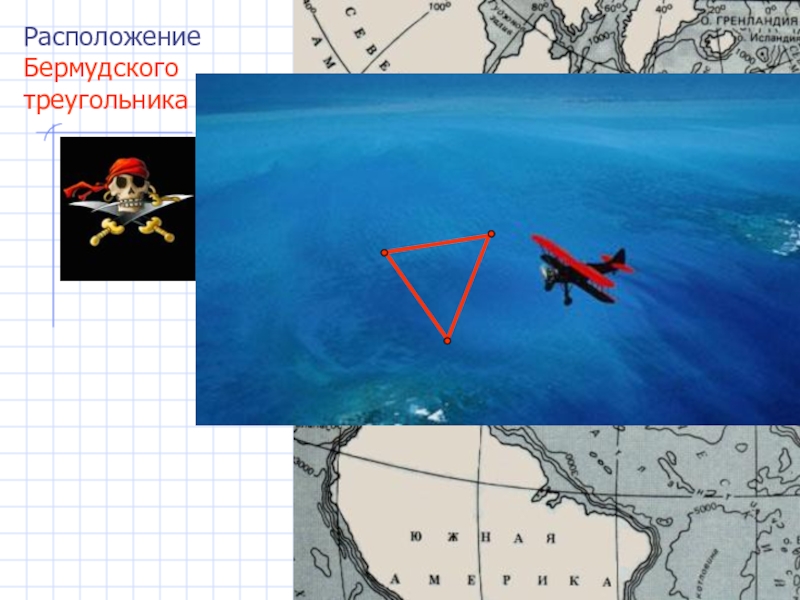
- 6. Расположение Бермудского треугольника
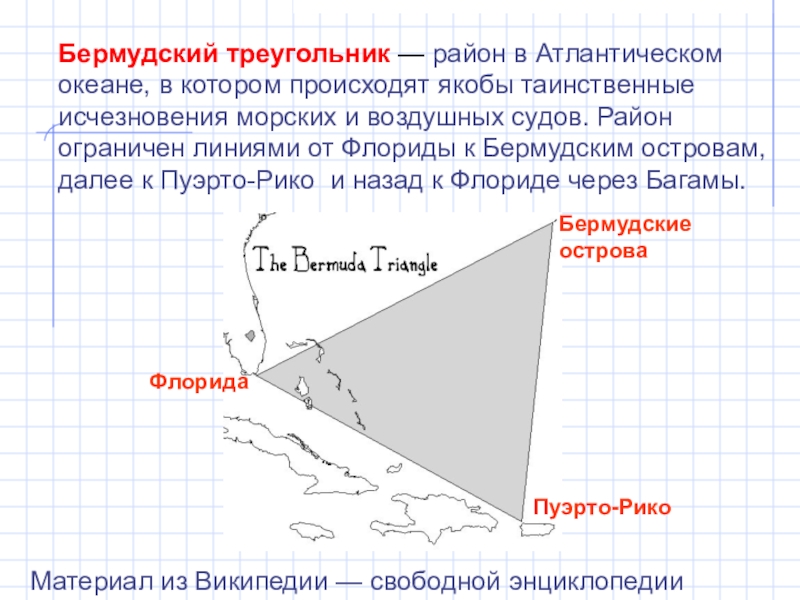
- 7. Бермудский треугольник — район в Атлантическом океане,
- 8. Скептики утверждают, однако, что
- 9. Две рейки, у которых два конца скреплены
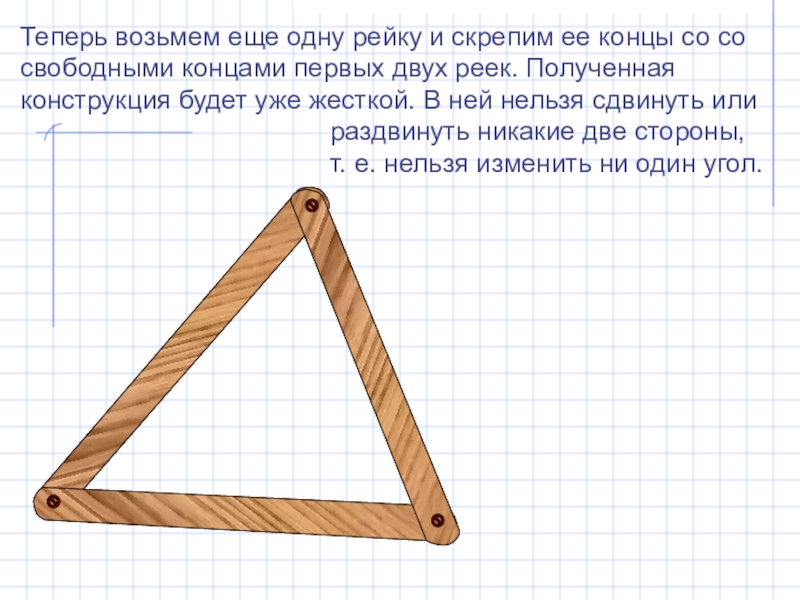
- 10. Теперь возьмем еще одну рейку и скрепим
- 11. Свойство жесткости треугольника широко используют в практике.
- 12. 19 марта 2007 года Шуховской башне на
- 13. Высоковольтные линии электропередачи.
- 14. Треугольники в конструкции мостов.
- 15. Для составления красивых паркетов использовали треугольники.
- 16. Треугольник полярный, треугольник характеристический. Каких только треугольников
- 17. С древних времен известен очень простой способ построения прямых углов на местности.
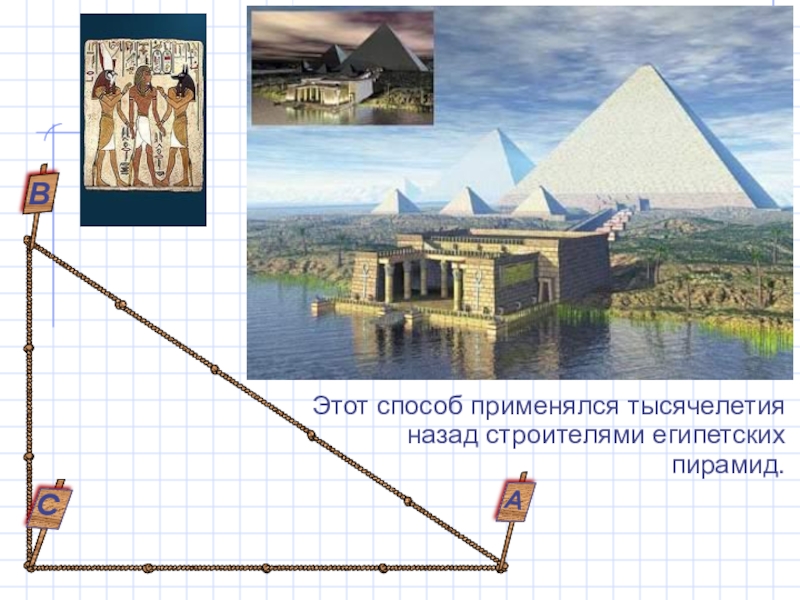
- 18. Этот способ применялся тысячелетия назад строителями египетских пирамид.СВ
- 19. Треугольник Паскаля.Устройство треугольника Паскаля: каждое число равно
- 20. Треугольник Паскаля компьютер перевёл на язык цвета.
- 21. Треугольник Паскаля компьютер перевёл на язык цвета.
- 22. Треугольник Пенроуза или трибар. Из коллекции
- 23. Треугольник из кубовГеометрические фигуры – лучший источник вдохновения
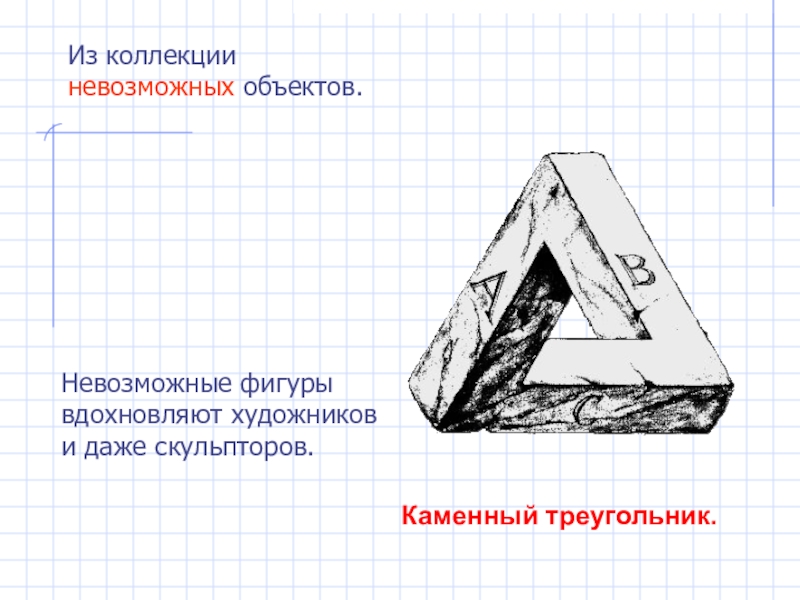
- 24. Каменный треугольник.Невозможные фигуры вдохновляют художников и даже скульпторов.Из коллекции невозможных объектов.
Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.
Слайд 2Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для
этого используют специальную треугольную рамку.
Слайд 4При расположении товара на прилавках супермаркета, обязательно учитывается правило «золотого треугольника»,
основанное на психологии покупателя.
Слайд 7Бермудский треугольник — район в Атлантическом океане, в котором происходят якобы
таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы.
Материал из Википедии — свободной энциклопедии
Пуэрто-Рико
Флорида
Бермудские
острова
Слайд 8 Скептики утверждают, однако, что
исчезновения судов в бермудском
треугольнике происходят не чаще,
чем в других районах мирового океана
и объясняются естественными
причинами. Такого же мнения
придерживается Береговая охрана
США и страховая компания Lloyd's.
Слайд 9
Две рейки, у которых два конца скреплены гвоздем.
Такая конструкция не является
жесткой: сдвигая или раздвигая концы, мы можем менять угол между ними.
Слайд 10
Теперь возьмем еще одну рейку и скрепим ее концы со со
свободными концами первых двух реек. Полученная конструкция будет уже жесткой. В ней нельзя сдвинуть или
раздвинуть никакие две стороны,
т. е. нельзя изменить ни один угол.
раздвинуть никакие две стороны,
т. е. нельзя изменить ни один угол.
Слайд 11
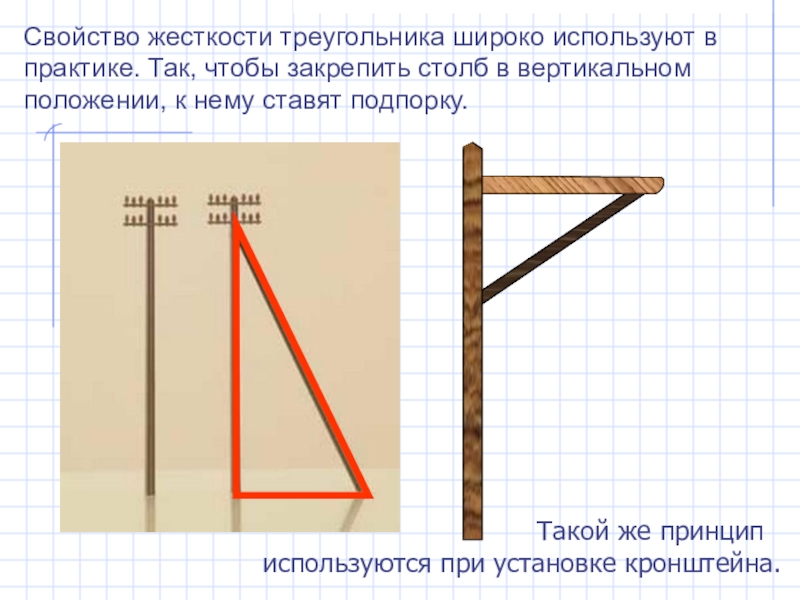
Свойство жесткости треугольника широко используют в практике. Так, чтобы закрепить столб
в вертикальном положении, к нему ставят подпорку.
Слайд 1219 марта 2007 года Шуховской башне на Шаболовке исполнилось 85 лет
Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций.
Слайд 16Треугольник полярный, треугольник характеристический. Каких только треугольников нет в математике.
В
глубокой древности вместе с астрономией появилась появилась наука – тригонометрия.
Слово «тригонометрия»
произведено от греческих
«треугольник»
«меряю»
Буквальное значение – «наука об измерении треугольников»
Слово «тригонометрия»
произведено от греческих
«треугольник»
«меряю»
Буквальное значение – «наука об измерении треугольников»
Слайд 19Треугольник
Паскаля.
Устройство треугольника Паскаля:
каждое число равно сумме двух расположенных над
ним чисел.
Все элементарно, но сколько в этом таится чудес.
Треугольник можно продолжать неограниченно.
Все элементарно, но сколько в этом таится чудес.
Треугольник можно продолжать неограниченно.
Замечательные треугольники
Слайд 22Треугольник
Пенроуза
или трибар.
Из коллекции невозможных объектов.
Кажется, что мы
видим три
бруска квадратного сечения,
соединенных в треугольник.
Если вы закроете любой
угол этой фигуры, то увидите,
что все три бруска соединены правильно. Но когда вы уберете руку с закрытого угла, то станет очевиден обман. Те два бруска, которые соединятся в этом угле,
не должны быть даже вблизи друг друга!
бруска квадратного сечения,
соединенных в треугольник.
Если вы закроете любой
угол этой фигуры, то увидите,
что все три бруска соединены правильно. Но когда вы уберете руку с закрытого угла, то станет очевиден обман. Те два бруска, которые соединятся в этом угле,
не должны быть даже вблизи друг друга!
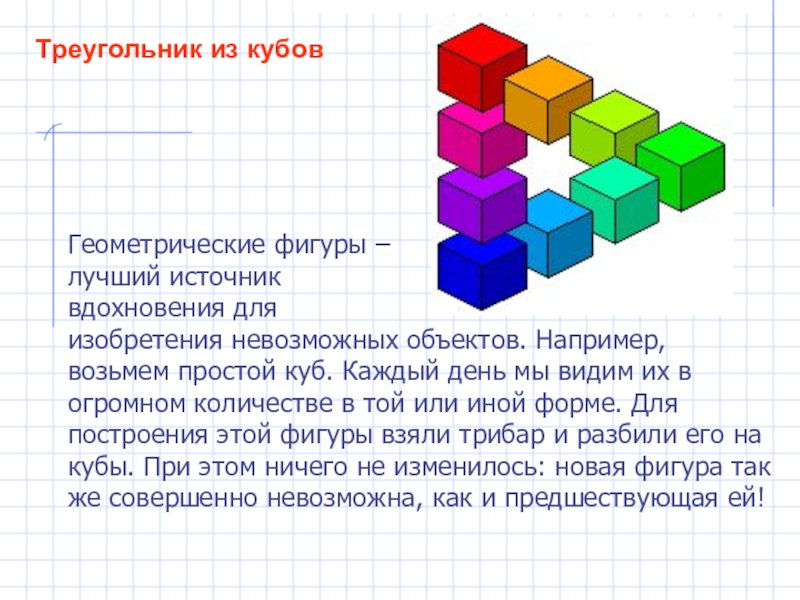
Слайд 23Треугольник из кубов
Геометрические фигуры –
лучший источник
вдохновения для
изобретения невозможных объектов.
Например, возьмем простой куб. Каждый день мы видим их в огромном количестве в той или иной форме. Для построения этой фигуры взяли трибар и разбили его на кубы. При этом ничего не изменилось: новая фигура так же совершенно невозможна, как и предшествующая ей!
Слайд 24Каменный треугольник.
Невозможные фигуры вдохновляют художников
и даже скульпторов.
Из коллекции
невозможных объектов.
