- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Угол между прямой и плоскостью (10 класс)
Содержание
- 1. Презентация по геометрии на тему Угол между прямой и плоскостью (10 класс)
- 2. Цели урока:ввести понятие угла между прямой и плоскостью;рассмотреть задачи, в которых используется это понятие.
- 3. Устная работасформулируйте теорему о трех перпендикулярах.
- 4. PKDНазовите перпендикуляр, основание перпендикуляра, наклонную к плоскости
- 5. Устная работачто называется расстоянием от точки A
- 6. Проекция точки на плоскостьMM1NПроекцией точки на плоскость
- 7. Проекция фигуры на плоскостьЕсли построить проекции всех
- 8. Проекция прямой на плоскостьM1Maa1HH1О
- 9. Угол между прямой и плоскостьюaa1AУглом между прямой
- 10. замечанияaa1aAЕсли a , то проекция a
- 11. Решение задач
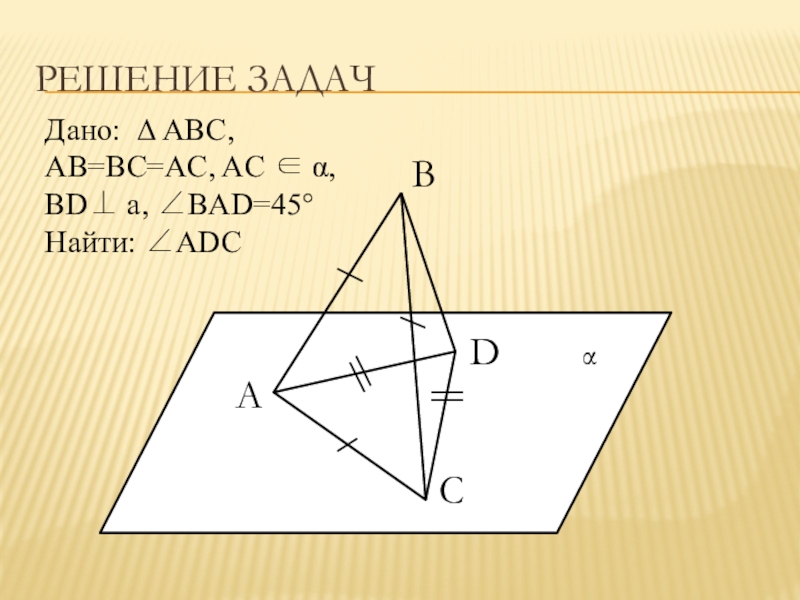
- 12. Решение задачBADCДано: ABC, AB=BC=AC, AC , BD a, ∠BAD=45°Найти: ∠ADC
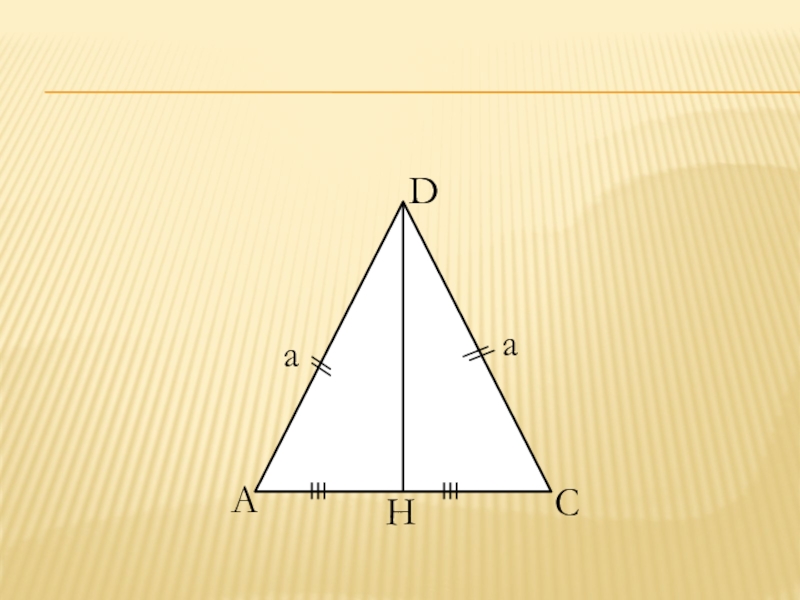
- 13. DACaaH
- 14. выводУгол между прямой и ее проекцией на
- 15. Домашнее заданиеП.21.№162, 163Найдите периметр прямоугольного треугольника, если
- 16. СПАСИБО ЗА ВНИМАНИЕ!
Цели урока:ввести понятие угла между прямой и плоскостью;рассмотреть задачи, в которых используется это понятие.
Слайд 2Цели урока:
ввести понятие угла между прямой и плоскостью;
рассмотреть задачи, в которых
используется это понятие.
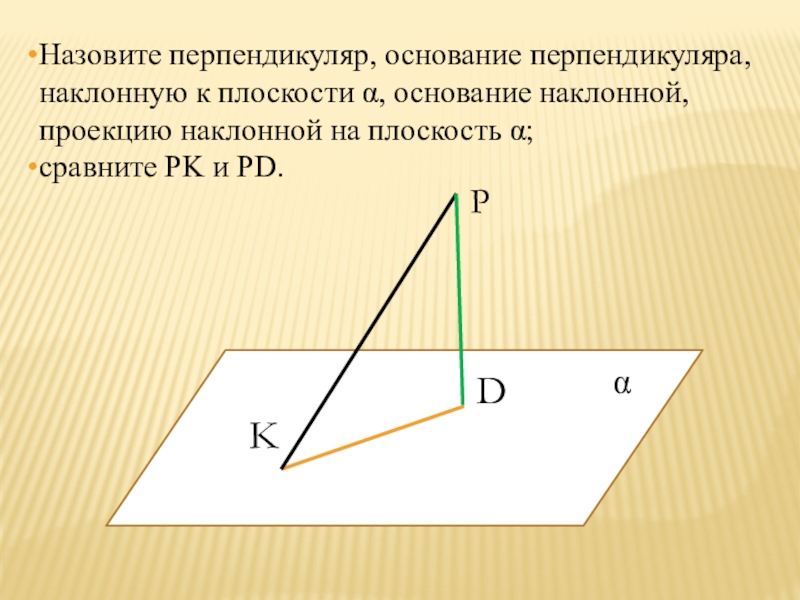
Слайд 4P
K
D
Назовите перпендикуляр, основание перпендикуляра, наклонную к плоскости , основание наклонной, проекцию
наклонной на плоскость ;
сравните PK и PD.
сравните PK и PD.
Слайд 5Устная работа
что называется расстоянием от точки A до плоскости ?
что называется
расстоянием между параллельными плоскостями?
что называется расстоянием между скрещивающимися прямыми?
что называется углом между прямыми?
что называется углом между скрещивающимися прямыми?
что называется расстоянием между скрещивающимися прямыми?
что называется углом между прямыми?
что называется углом между скрещивающимися прямыми?
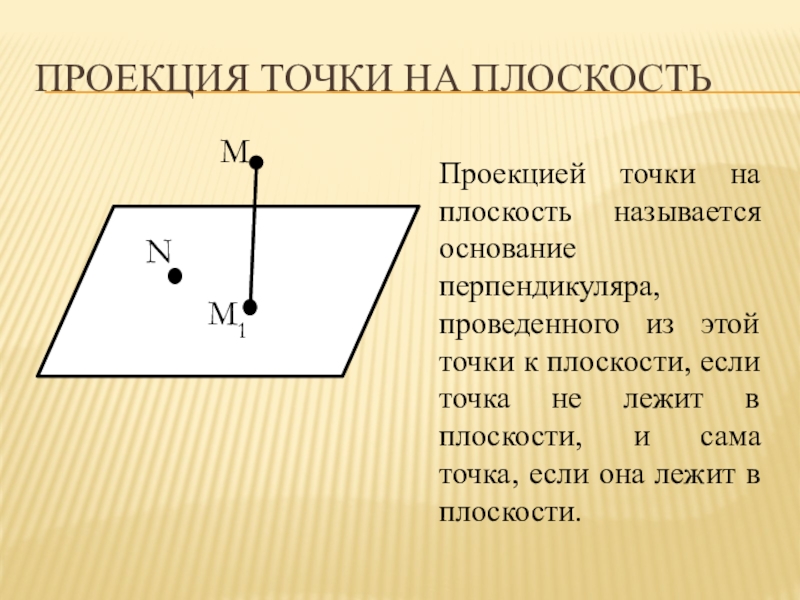
Слайд 6Проекция точки на плоскость
M
M1
N
Проекцией точки на плоскость называется основание перпендикуляра, проведенного
из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
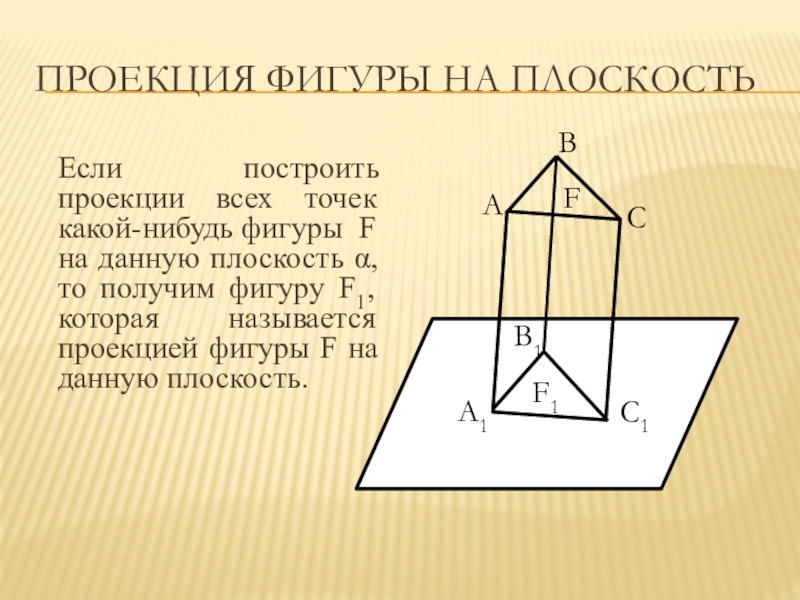
Слайд 7Проекция фигуры на плоскость
Если построить проекции всех точек какой-нибудь фигуры F
на данную плоскость , то получим фигуру F1, которая называется проекцией фигуры F на данную плоскость.
A1
A
B
C
F
A1
C1
B1
F1
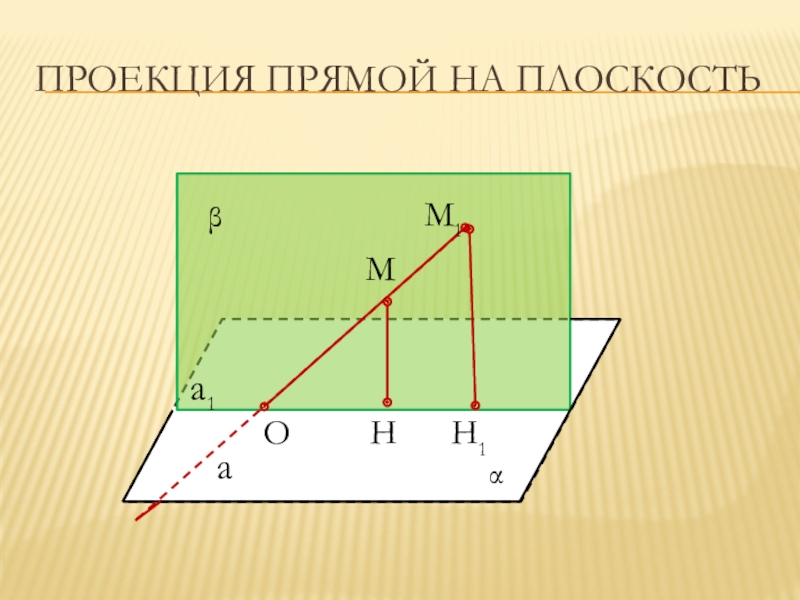
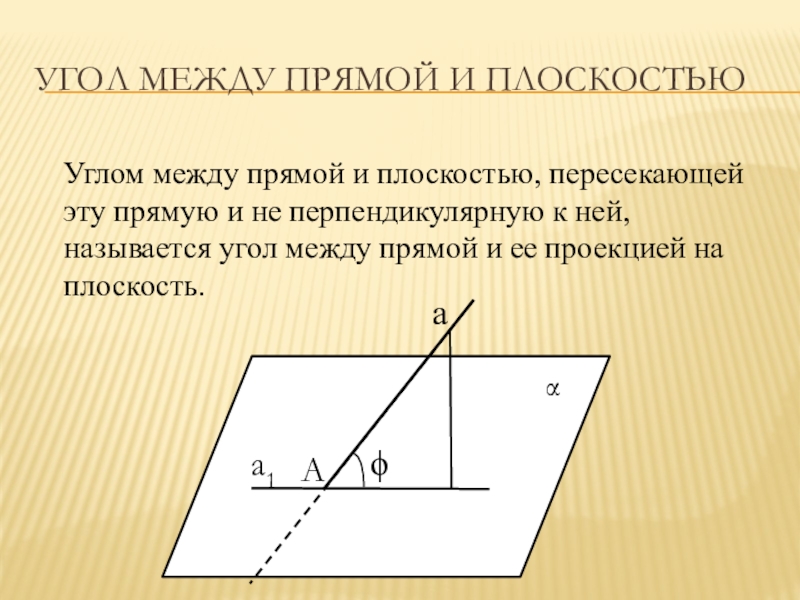
Слайд 9Угол между прямой и плоскостью
a
a1
A
Углом между прямой и плоскостью, пересекающей эту
прямую и не перпендикулярную к ней, называется угол между прямой и ее проекцией на плоскость.
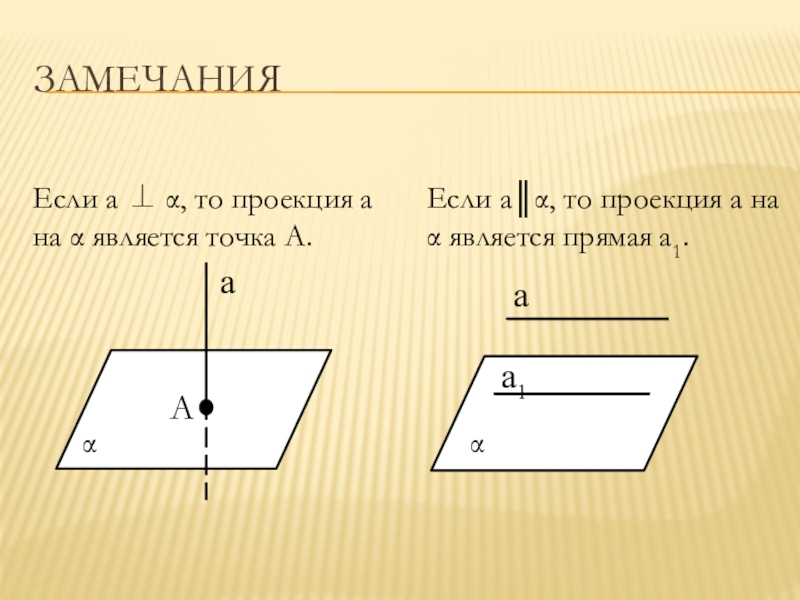
Слайд 10замечания
a
a1
a
A
Если a , то проекция a на является точка
А.
Если a║, то проекция a на является прямая a1.
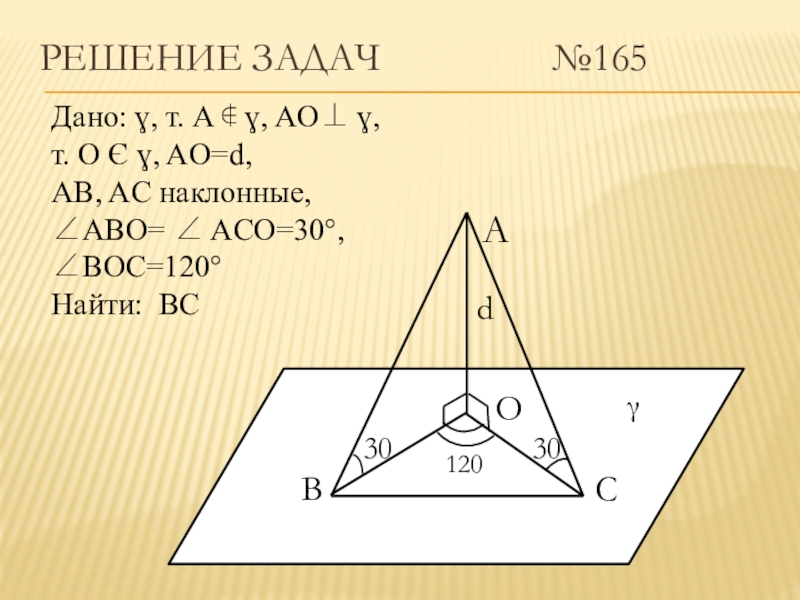
Слайд 11Решение задач №165
A
30
30
B
C
O
Дано:
ɣ, т. A ∉ ɣ, AO ɣ,
т. О Є ɣ, AO=d,
AB, AC наклонные,
∠ABO= ∠ ACO=30°, ∠BOC=120°
Найти: BC
Найти: BC
Слайд 14вывод
Угол между прямой и ее проекцией на плоскость есть наименьший из
углов данной прямой и прямыми, лежащими в этой плоскости и проходящими через точку пересечения данной прямой с плоскостью.
Слайд 15Домашнее задание
П.21.
№162, 163
Найдите периметр прямоугольного треугольника, если радиус вписанной окружности равен
1, а радиус описанной окружности равен 2,5.