- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Углы в прямоугольном треугольнике
Содержание
- 1. Презентация по геометрии на тему Углы в прямоугольном треугольнике
- 2. Вспомним Sin A = cos B Cos
- 3. Задача №1В треугольнике АВС угол С равен 90°, sinA= 7/25. Найдите cosA . Решение.Ответ: 0,96.
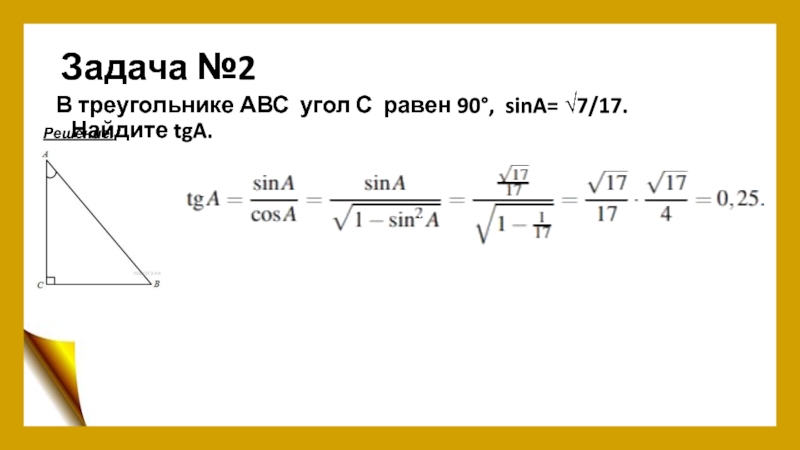
- 4. Задача №2В треугольнике АВС угол С равен 90°, sinA= √7/17. Найдите tgA.Решение.
- 5. Задача №3В треугольнике АВС угол С равен 90°, sinA= 7/25. Найдите sinB.Решение.
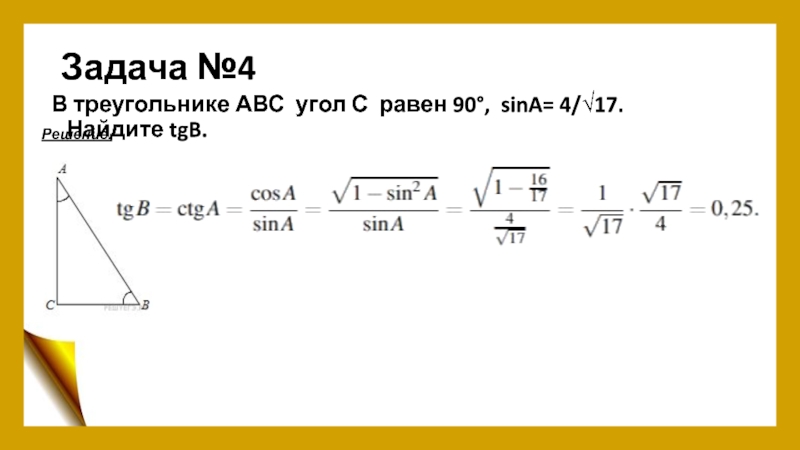
- 6. Задача №4В треугольнике АВС угол С равен 90°, sinA= 4/√17. Найдите tgB.Решение.
- 7. Задача №5В треугольнике АВС угол С равен 90°, tgA= 7/24. Найдите sinA.Решение.
- 8. Задача №6В треугольнике АВС угол С равен 90°, tgA= 2. Найдите tgB.Решение.
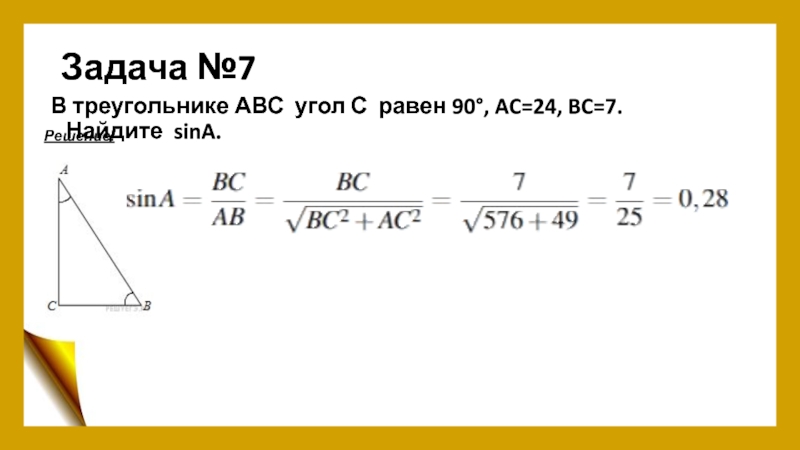
- 9. Задача №7В треугольнике АВС угол С равен 90°, AC=24, BC=7. Найдите sinA.Решение.
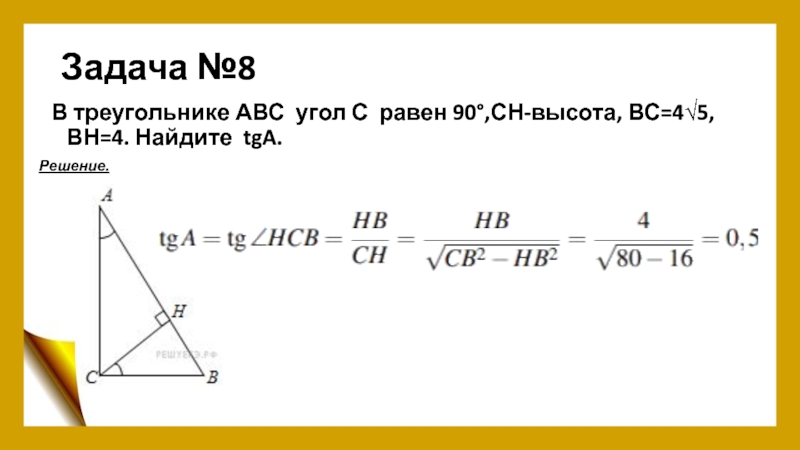
- 10. Задача №8В треугольнике АВС угол С равен 90°,СН-высота, ВС=4√5, ВН=4. Найдите tgA.Решение.
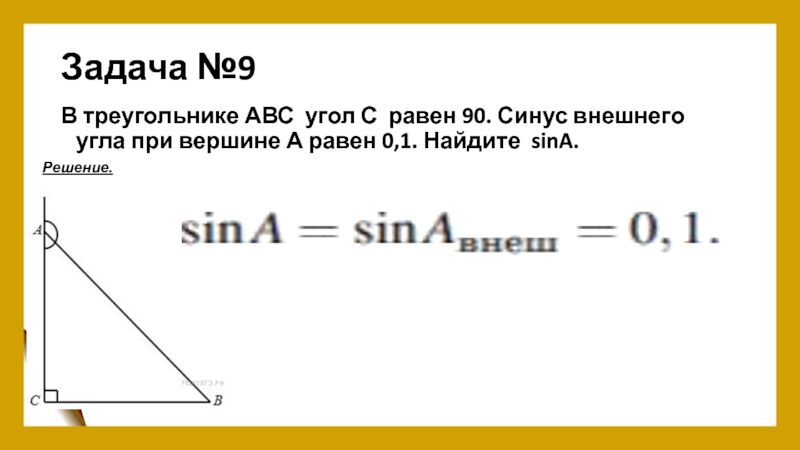
- 11. Задача №9В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине А равен 0,1. Найдите sinA.Решение.
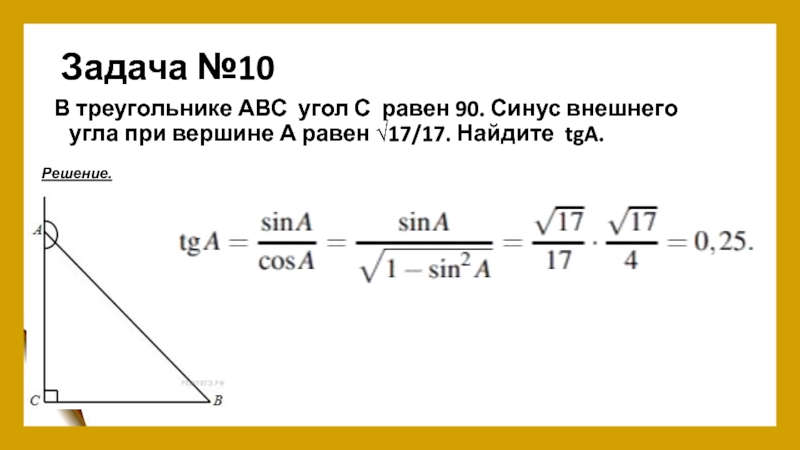
- 12. Задача №10В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине А равен √17/17. Найдите tgA.Решение.
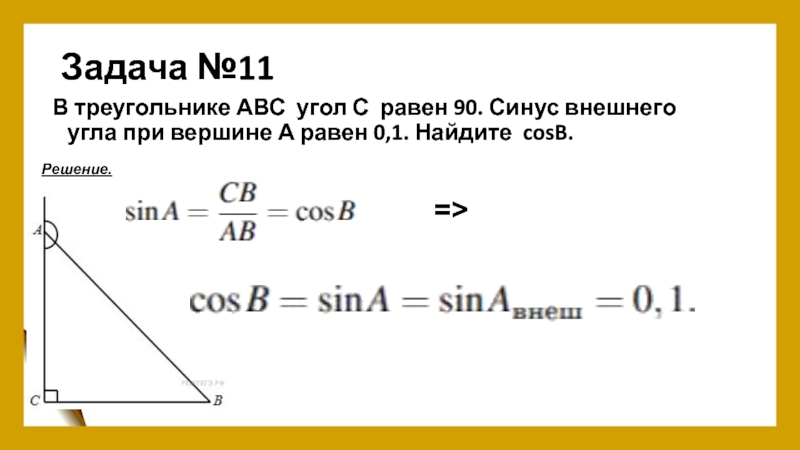
- 13. Задача №11В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине А равен 0,1. Найдите cosB.Решение.=>
- 14. Задача №12 Один острый
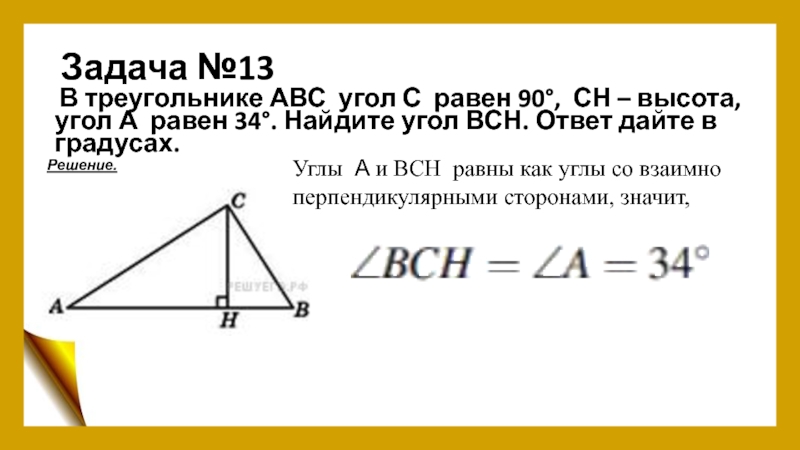
- 15. Задача №13 В треугольнике АВС угол С равен
- 16. Задача №14Острые углы прямоугольного треугольника равны 85°
- 17. Задача №15Острые углы прямоугольного треугольника равны 62°
- 18. Задача №16В треугольнике АВС угол С равен 90, tg
- 19. Шаблон подготовлен учителем русского языка и литературы
Слайд 2Вспомним
Sin A = cos B
Cos A = sin B
tg A = ctg B
Sin A = Sin внеш. A
Cos A = - Cos внеш. A
tg A = - tg внеш. A
В прямоугольном треугольнике ABC,
с прямым углом С:
Слайд 3Задача №1
В треугольнике АВС угол С равен 90°, sinA= 7/25. Найдите cosA .
Решение.
Ответ:
Слайд 11Задача №9
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине
Решение.
Слайд 12Задача №10
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине
Решение.
Слайд 13Задача №11
В треугольнике АВС угол С равен 90. Синус внешнего угла при вершине
Решение.
=>
Слайд 14Задача №12
Один острый угол прямоугольного треугольника на
Решение.
Сумма острых углов прямоугольного треугольника равна 90°, значит, если меньший из них обозначить за Х, то другой будет (Х+32°).
Тогда: Х+(Х+32°) = 90° => 2Х=90°- 32°
2Х =58°, т.е. Х=29°. Значит больший угол равен 29°+32°= 61°
Слайд 15Задача №13
В треугольнике АВС угол С равен 90°, СН – высота, угол А равен
Решение.
Углы А и ВСН равны как углы со взаимно
перпендикулярными сторонами, значит,
Слайд 16Задача №14
Острые углы прямоугольного треугольника равны 85° и 5°. Найдите угол
Решение.
Углы САН и ВАС равны, как углы сo
взаимно перпендикулярными сторонами.
Из прямоугольного треугольника DCH:
Слайд 17Задача №15
Острые углы прямоугольного треугольника равны 62° и 28°. Найдите угол
Решение.
Медиана, проведённая к гипотенузе, равна её
половине, поэтому треугольник ACF –
равнобедренный. Тогда угол АСF=28°.
Поскольку CH — высота, то угол ВСН=90°-62°=28°.
Поэтому для искомого угла имеем:
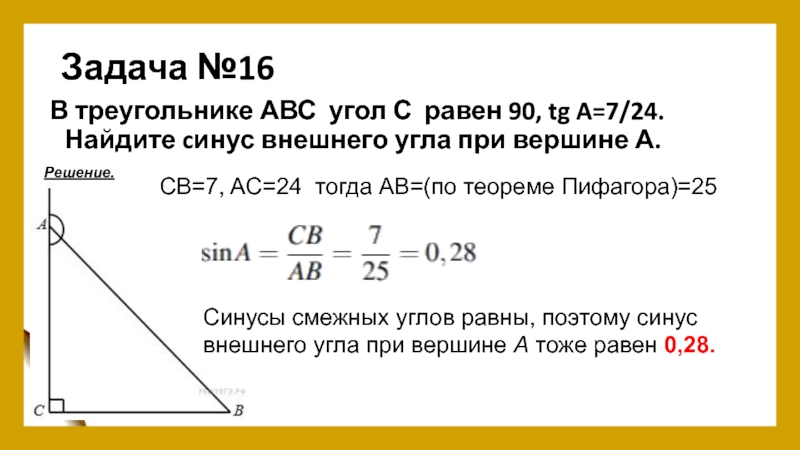
Слайд 18Задача №16
В треугольнике АВС угол С равен 90, tg A=7/24. Найдите cинус внешнего
Решение.
CB=7, AC=24 тогда АВ=(по теореме Пифагора)=25
Синусы смежных углов равны, поэтому синус
внешнего угла при вершине А тоже равен 0,28.