- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Цилиндр(11 класс)
Содержание
- 1. Презентация по геометрии на тему Цилиндр(11 класс)
- 2. Это- окружностьОКРУЖНОСТЬ –замкнутая линия, все точки которой равноудалены от точки О (центра окружности).О
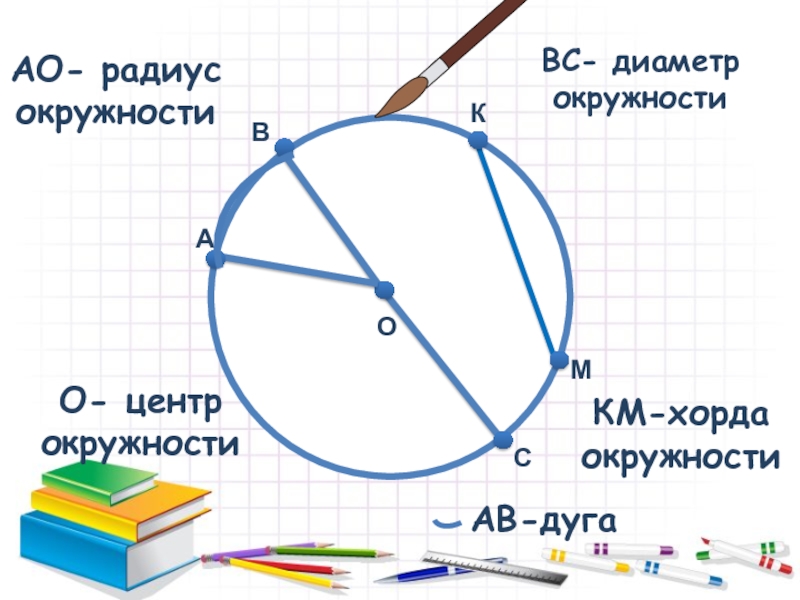
- 3. АО- радиус окружностиOBВC- диаметр окружностиCКМКМ-хорда окружностиАО- центр окружностиАВ-дуга
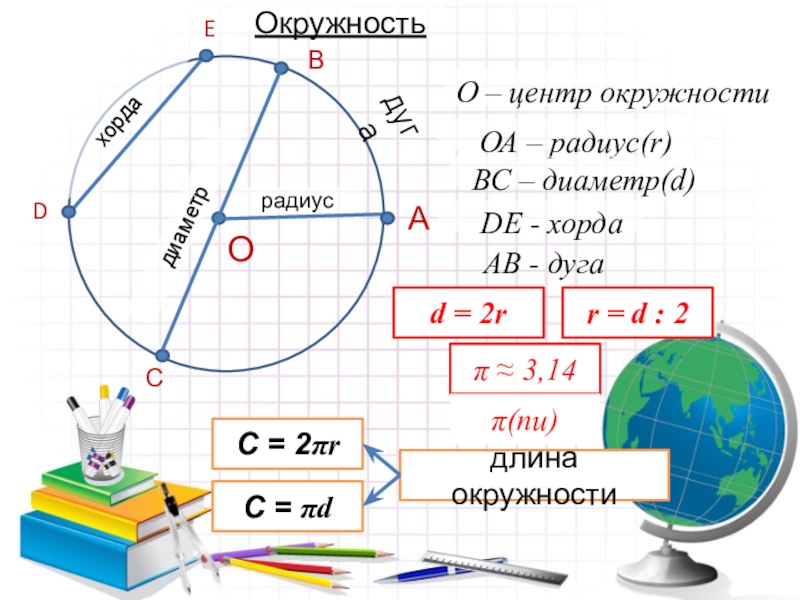
- 4. ОрадиусВDСА ОА – радиус(r)ОкружностьО – центр окружностиВС
- 5. Это- кругКруг–часть плоскости, ограниченная окружностью.Sкр. = πR2
- 6. Цилиндр
- 7. Тело, которое состоит из двух кругов, лежащих
- 8. Слайд 8
- 9. Элементы цилиндра:
- 10. ЭЛЕМЕНТЫ ЦИЛИНДРААВ- образующая цилиндраОО1- высота(ось) цилиндраВО- радиус цилиндра
- 11. Назовите и покажите элементы цилиндра.
- 12. ВИДЫ СЕЧЕНИЙОсевое сечение цилиндраСечение цилиндра плоскостью, перпендикулярной к оси.Сечение цилиндра плоскостью, параллельной оси.
- 13. Если секущая плоскость проходит через ось цилиндра,
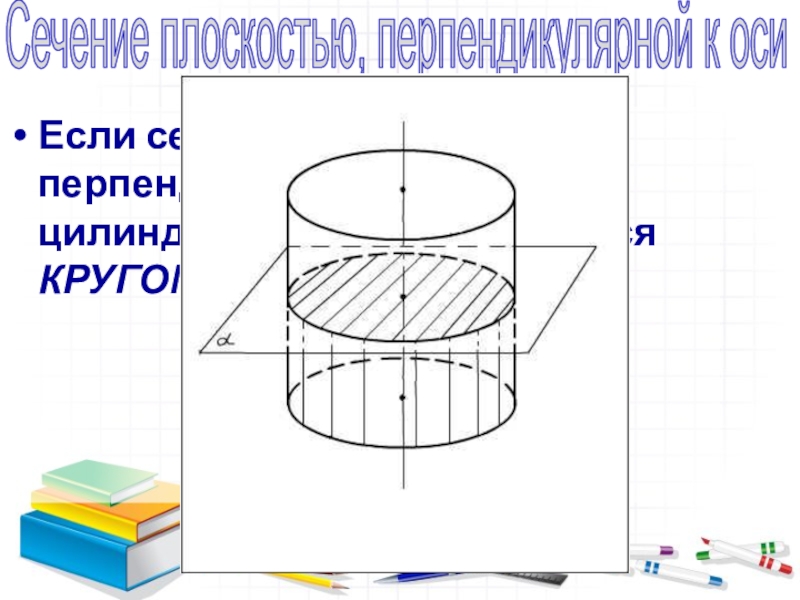
- 14. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является КРУГОМ.Сечение плоскостью, перпендикулярной к оси
- 15. Если секущая плоскость проходит параллельно оси цилиндра,
- 16. Цилиндр может быть получен вращением
- 17. Представим себе, что боковую поверхность
- 18. Этот прямоугольник называется развёрткой боковой
- 19. Площадью полной поверхности цилиндра называется
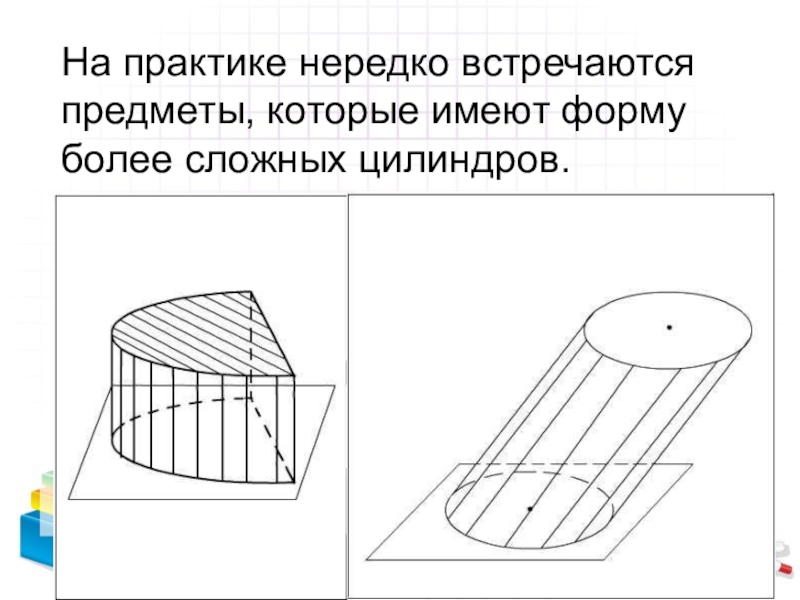
- 20. На практике нередко встречаются предметы, которые имеют форму более сложных цилиндров.
- 21. 24.01.17 г. Классная
- 22. №2. У цилиндра радиус основания и высота
- 23. Д/з. выучить правила, №523, 527
- 24. Что такое прямой круговой цилиндр (образующая цилиндра,
- 25. Слайд 25
Это- окружностьОКРУЖНОСТЬ –замкнутая линия, все точки которой равноудалены от точки О (центра окружности).О
Слайд 2Это- окружность
ОКРУЖНОСТЬ –замкнутая линия, все точки которой равноудалены от точки О
(центра окружности).
О
Слайд 3АО- радиус окружности
O
B
ВC- диаметр окружности
C
К
М
КМ-хорда окружности
А
О- центр окружности
АВ-дуга
Слайд 4О
радиус
В
D
С
А
ОА – радиус(r)
Окружность
О – центр окружности
ВС – диаметр(d)
E
DE
- хорда
хорда
диаметр
C = 2πr
C = πd
длина окружности
АВ - дуга
дуга
π ≈ 3,14
π(пи)
r = d : 2
d = 2r
Слайд 7 Тело, которое состоит из двух кругов, лежащих в параллельных плоскостях, и
всех отрезков, соединяющие соответственные точки этих кругов, называется цилиндром.
Слайд 12ВИДЫ СЕЧЕНИЙ
Осевое сечение цилиндра
Сечение цилиндра плоскостью, перпендикулярной к оси.
Сечение цилиндра плоскостью,
параллельной оси.
Слайд 13Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой
ПРЯМОУГОЛЬНИК, две стороны которого- образующие, а две другие- диаметры оснований цилиндра.
Осевое сечение
Слайд 14Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является КРУГОМ.
Сечение
плоскостью, перпендикулярной к оси
Слайд 15Если секущая плоскость проходит параллельно оси цилиндра, то сечение- ПРЯМОУГОЛЬНИК, две
стороны которого- образующие, а две другие- хорды.
Сечение, параллельное оси
Слайд 16 Цилиндр может быть получен вращением прямоугольника вокруг одной из
его сторон. На рисунке изображён цилиндр, полученный вращением прямоугольника вокруг стороны АВ. При этом боковая поверхность цилиндра образуется вращением стороны CD, а основания- вращением сторон BC и AD.
Цилиндр- тело вращения
Слайд 17 Представим себе, что боковую поверхность цилиндра разрезали по образующей
и развернули таким образом, что все образующие оказались в одной плоскости.
Площадь поверхности цилиндра
Слайд 18 Этот прямоугольник называется развёрткой боковой поверхности цилиндра.
За
площадь боковой поверхности цилиндра принимается площадь её развёртки.
Sбок. = 2πRH
Sбок. = 2πRH
Слайд 19 Площадью полной поверхности цилиндра называется сумма площадей двух оснований
и
боковой поверхности
боковой поверхности
Площадь полной поверхности
Sполн. = 2•Sосн. + Sбок.
Sбок. = 2πRH
Sосн. = πR2
Слайд 21 24.01.17 г. Классная работа
Цилиндр и его сечения
№1.Длина отрезка, концы которого находятся на кругах оснований цилиндра и который пересекает ось, равняется 13 см. Найдите радиус цилиндра, если его высота равняется 5 см.
Дано: цилиндр,
= 5 см,
= 13 см
Найти:
Решение.
Слайд 22№2. У цилиндра радиус основания и высота соответственно равны 6 см
и 5 см. Найдите:
а) диаметр основания цилиндра
б) диагональ осевого сечения цилиндра
в) угол наклона диагонали осевого сечения к плоскости основания
г) площадь основания цилиндра
д) площадь осевого сечения
е) полную поверхность цилиндра.
Слайд 24Что такое прямой круговой цилиндр (образующая цилиндра, основания цилиндра, боковая поверхность
цилиндра, радиус цилиндра, ось цилиндра, осевое сечение цилиндра)?
Заполните пропуски:
а)основания цилиндра лежат в ... плоскостях;
б)образующие цилиндра ... и ...;
в)поверхность цилиндра состоит из ... и ...;
г)прямой круговой цилиндр — это тело, которое описывает прямоугольник при обращении его вокруг ... как оси;
д)радиус цилиндра — это радиус ...;
е) высотой цилиндра называется расстояние между...
