: «Цилиндр»
учителя математики
ГБОУ СОШ №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Цилиндр
Содержание
- 1. Презентация по геометрии на тему Цилиндр
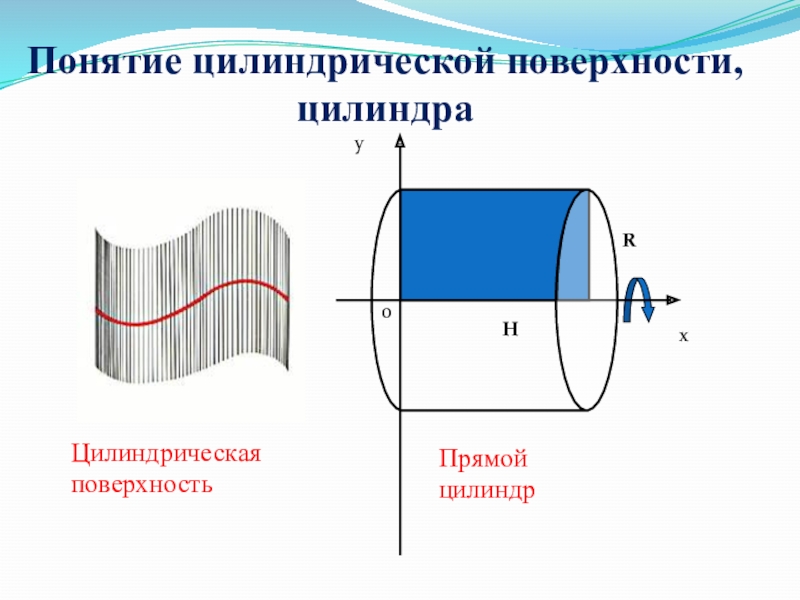
- 2. Понятие цилиндрической поверхности, цилиндра
- 3. Слайд 3
- 4. Слайд 4
- 5. Цилиндрическая архитектура
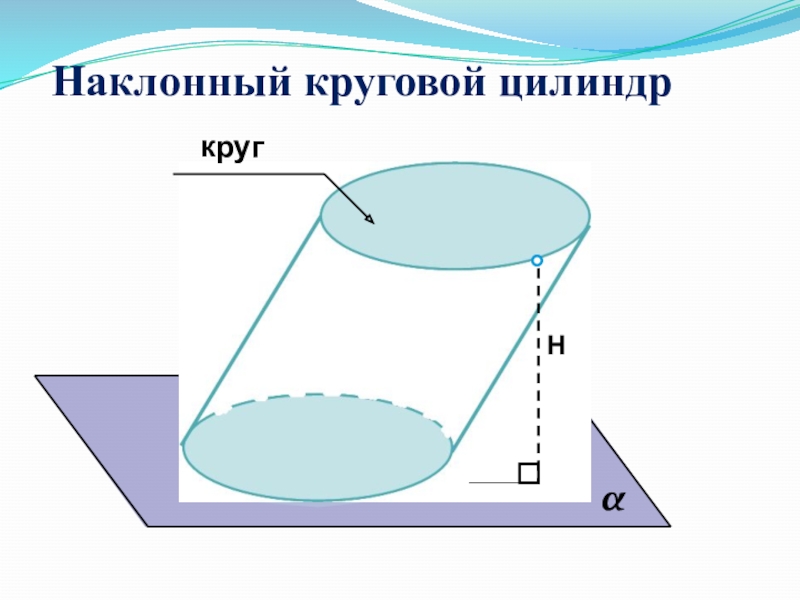
- 6. Наклонный круговой цилиндрНкруг
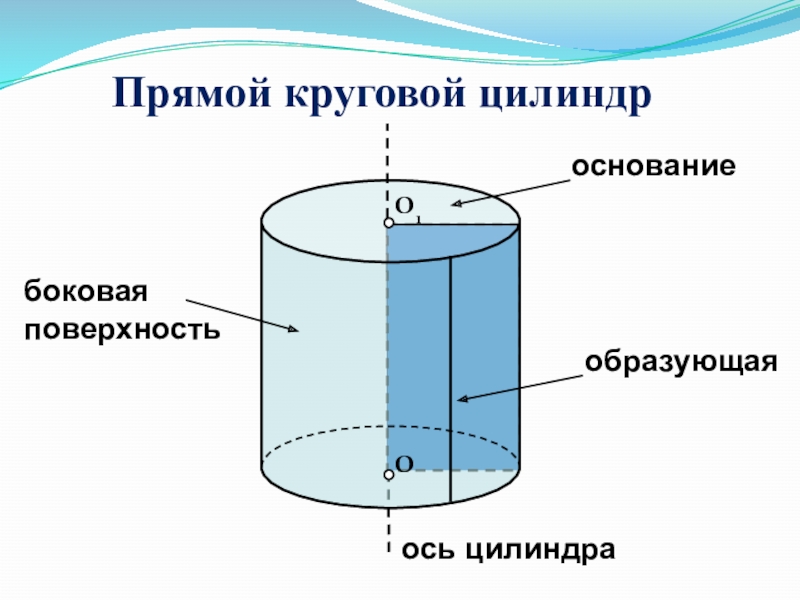
- 7. ОО1Прямой круговой цилиндроснованиеобразующаяось цилиндрабоковая поверхность
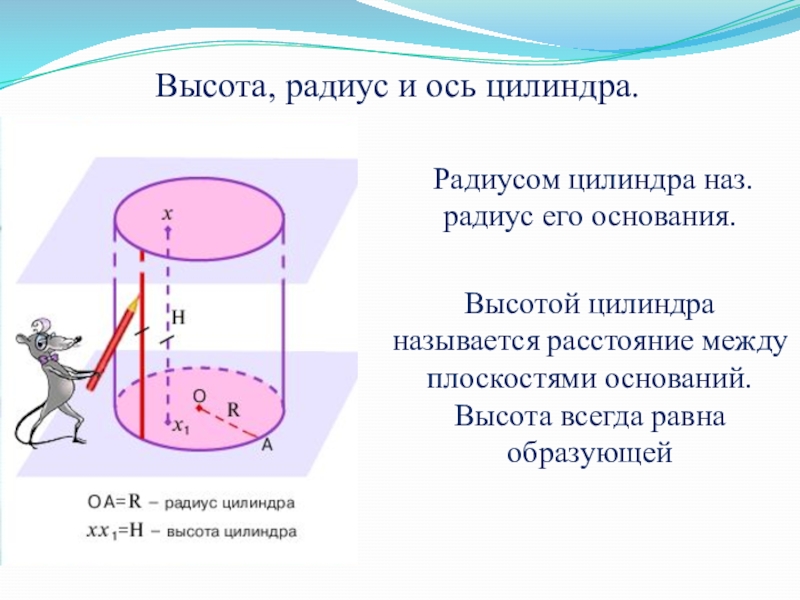
- 8. Высота, радиус и ось цилиндра. Радиусом
- 9. Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра, радиус которого равен 2.4
- 10. Понятие цилиндрической поверхности, цилиндраху0НRПрямой цилиндрЦилиндрическаяповерхность
- 11. Сечения цилиндра
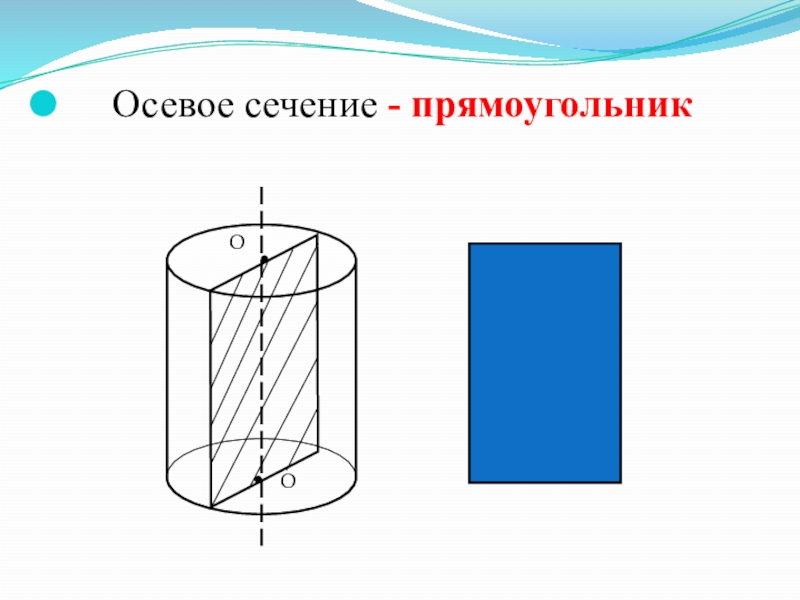
- 12. Осевое сечение - прямоугольникОО
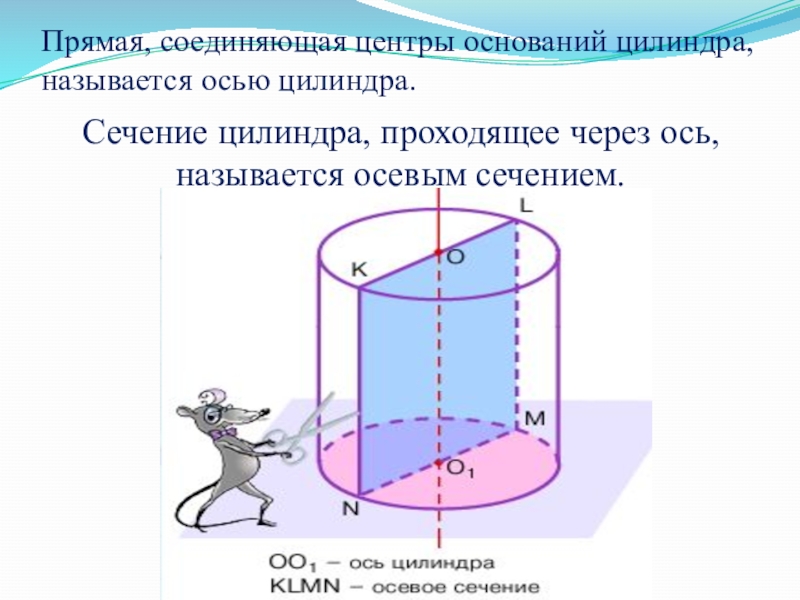
- 13. Прямая, соединяющая центры оснований цилиндра, называется осью цилиндра.Сечение цилиндра, проходящее через ось, называется осевым сечением.
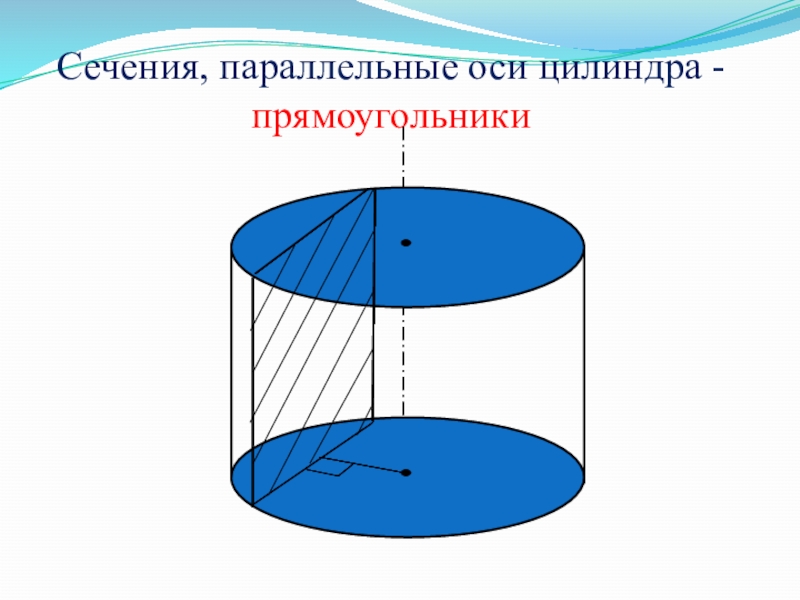
- 14. Сечения, параллельные оси цилиндра - прямоугольники
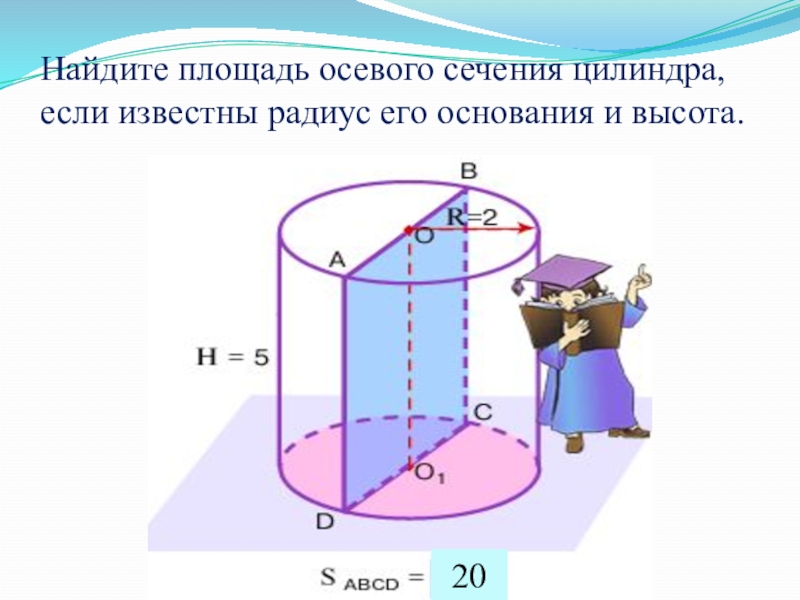
- 15. Найдите площадь осевого сечения цилиндра, если известны радиус его основания и высота.20
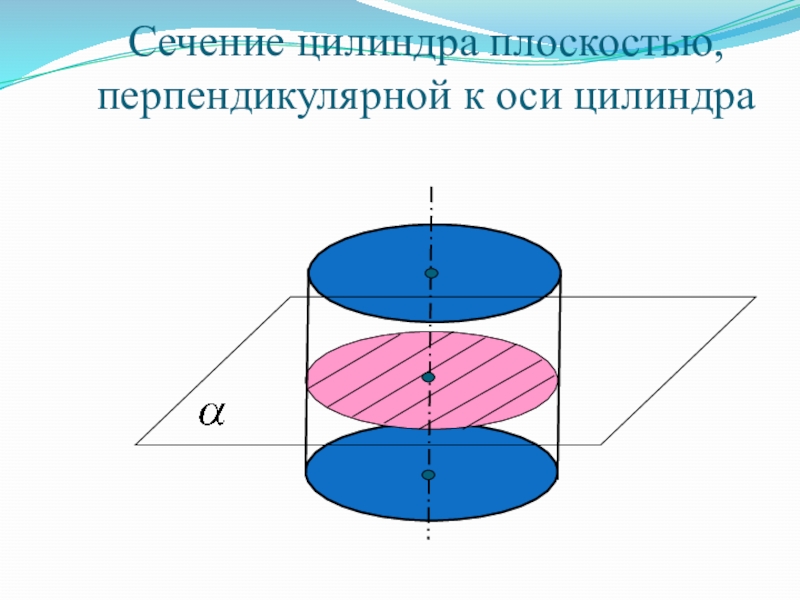
- 16. Сечение цилиндра плоскостью, перпендикулярной к оси цилиндра
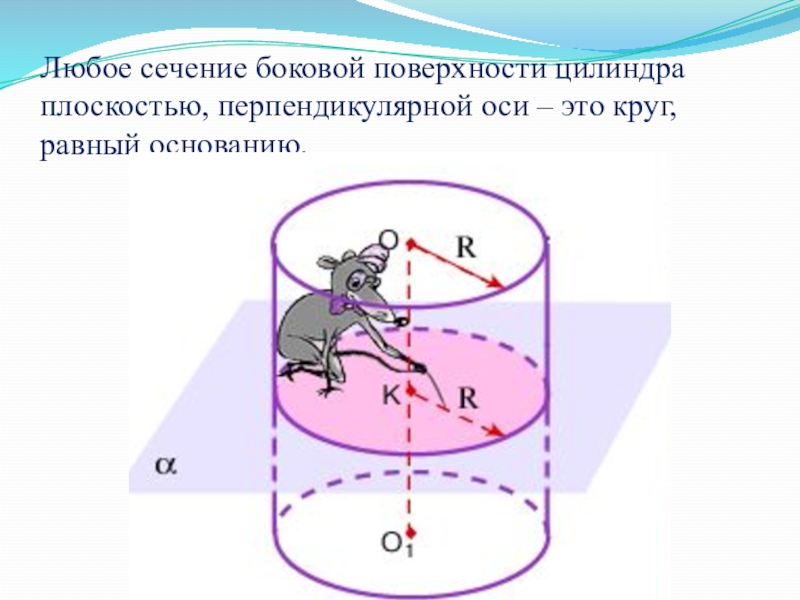
- 17. Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это круг, равный основанию.
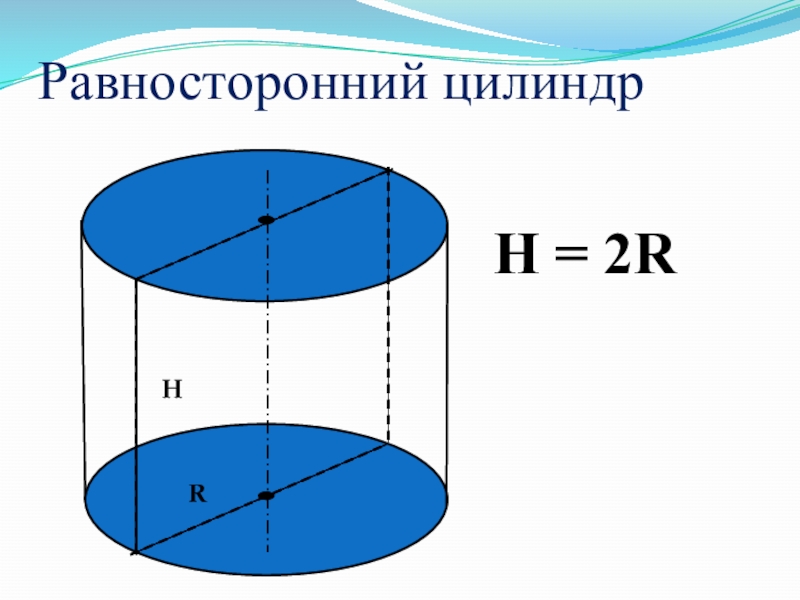
- 18. Равносторонний цилиндр
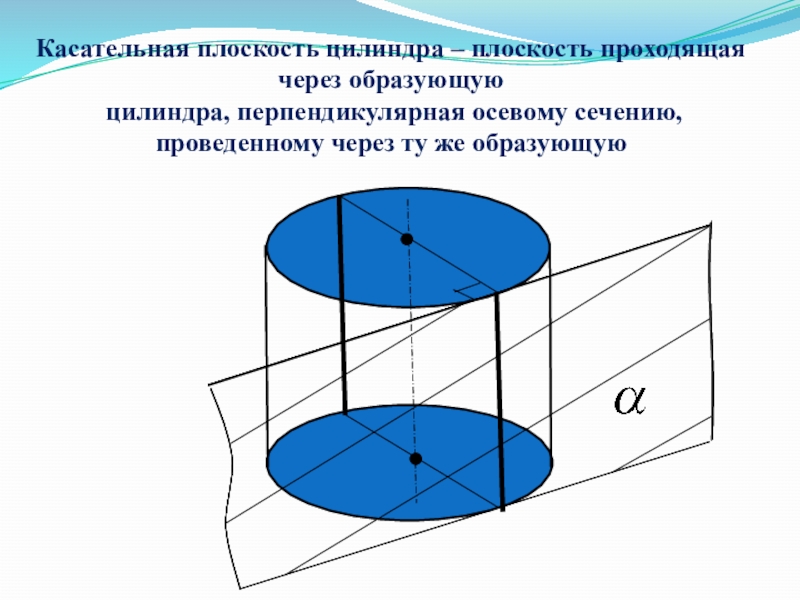
- 19. Касательная плоскость цилиндра – плоскость проходящая через
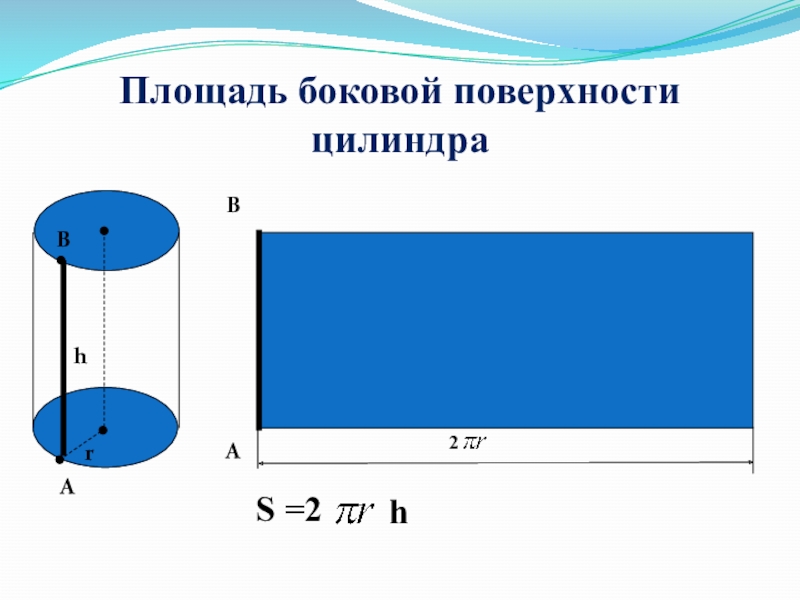
- 20. Площадь боковой поверхности цилиндраААВВhrS =2 h2
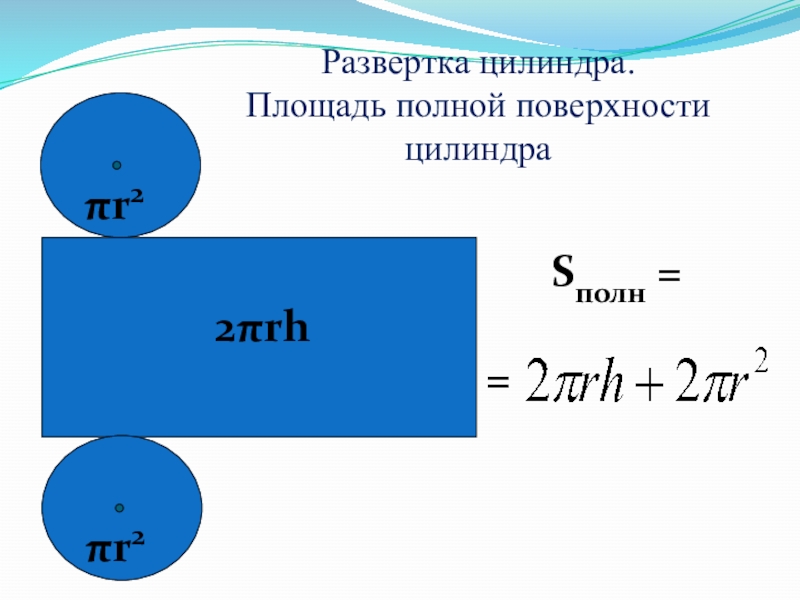
- 21. Развертка цилиндра. Площадь полной поверхности цилиндраSполн = =πr2πr22πrh
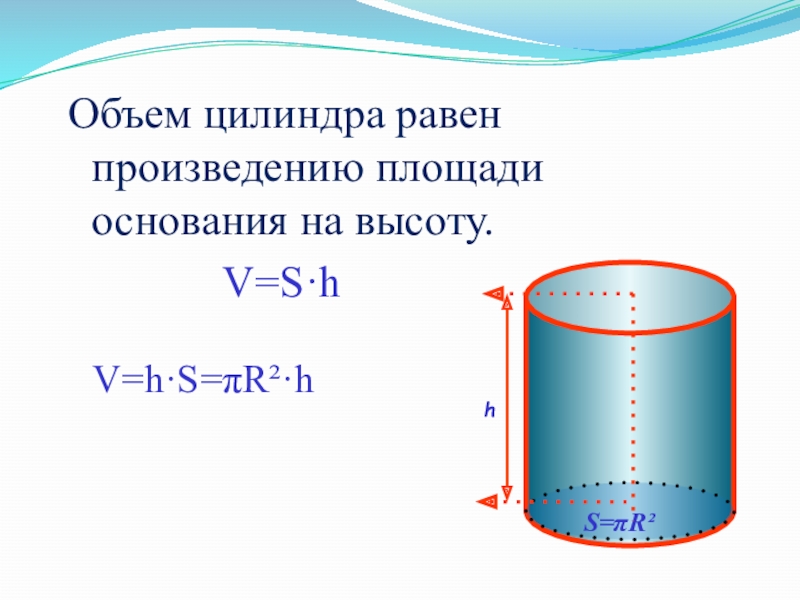
- 22. Объем цилиндра равен произведению площади основания на
- 23. Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке.
- 24. 1) Если дно шляпы опустить на плоскость
- 25. Осевое сечение цилиндра – квадрат, диагональ которого
- 26. Решение.1. Проведем диагональ АС сечения АВСD.ABCD2. ADC
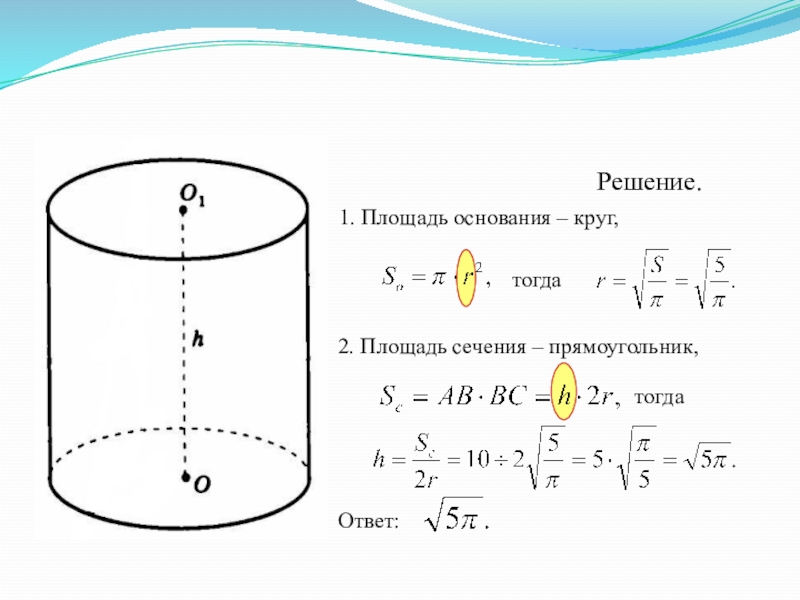
- 27. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания – 5 м2. Найдите высоту цилиндра.
- 28. Решение.1. Площадь основания – круг,тогда 2. Площадь сечения – прямоугольник,тогда Ответ:
- 29. Концы отрезка АВ лежат на разных основаниях
- 30. raРешение.1. Построим отрезок АВ.2. Проведем радиус АО.3.
- 31. rardКСПостроим отрезок d (расстояние между скрещивающимися прямыми
- 32. Через образующую АА1 цилиндра проведены две секущие
- 33. AА1C1В1ВCРешение.1) Сделаем чертеж, построим плоскости АА1В1В и
- 34. Найти площадь полной поверхности цилиндраАВС45ºАВС- прямоугольныйАВС- равнобедренный5ВС=АС=5r=2,5S=2π·2,5(5 + 2,5)= 5π·7,5 = 37,5πАВСS=2πr(h+r)АВСАВСr
- 35. Площадь осевого сечения цилиндра равна 10
- 36. АВСDOO1RHR=H=м
- 37. Высота цилиндра равна 8 см, радиус
- 38. OO1ABCDKABCD-прямоугольникSABCD= AB·AD, H=AB=8 см.HOK- расстояние от О
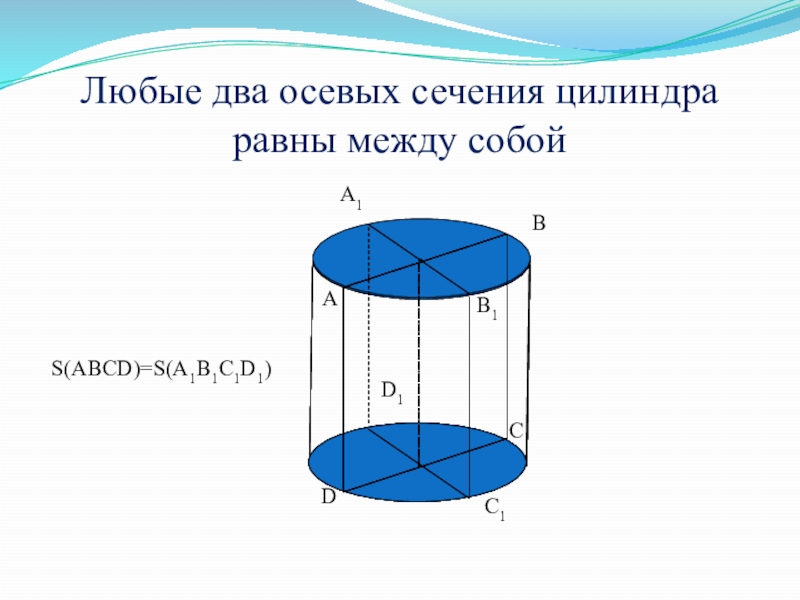
- 39. Любые два осевых сечения цилиндра равны между собойABCDA1B1C1D1S(ABCD)=S(A1B1C1D1)
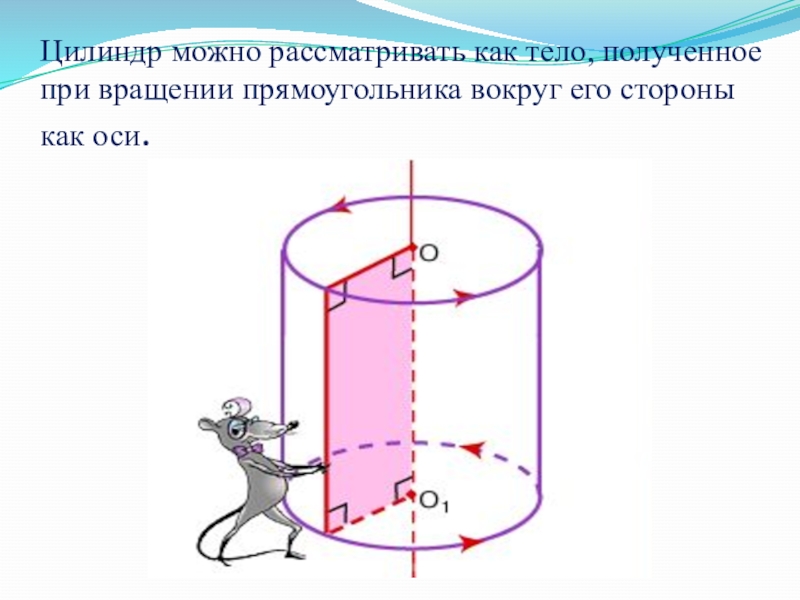
- 40. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси.
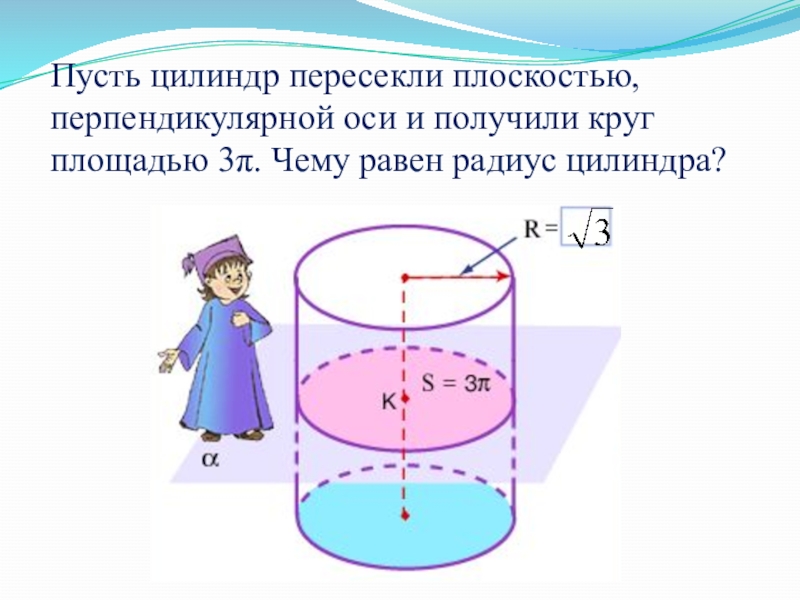
- 41. Пусть цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью 3π. Чему равен радиус цилиндра?
- 42. Высота цилиндра 7 см, а радиус основания
- 43. Дано: цилиндр; Н = 7, R =
- 44. Проведем дополнительное построение: построим высоту трапеции, ее
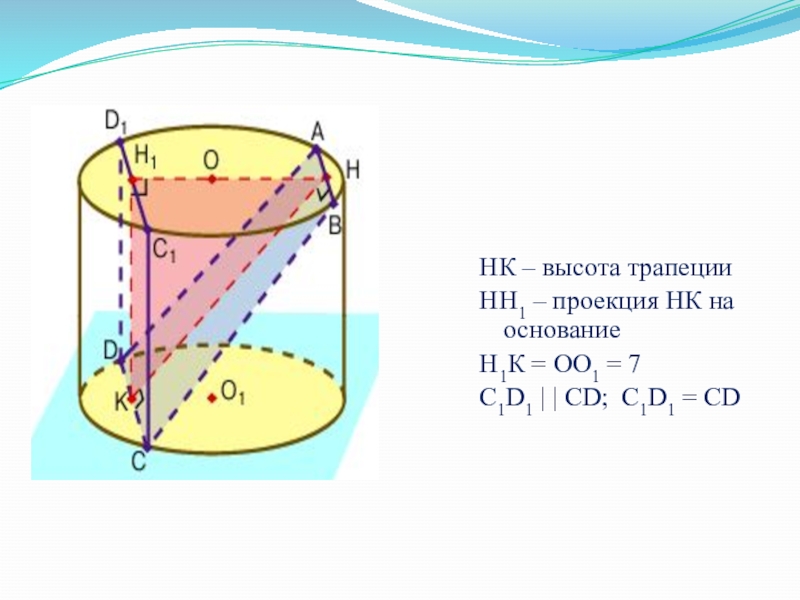
- 45. НК – высота трапецииНН1 – проекция НК
- 46. Рассмотрим проекцию высоты трапеции на верхнее основание
- 47. Найдем высоту трапеции, ее площадь и искомый
- 48. Задача для самостоятельного решения. Расстояние от
Понятие цилиндрической поверхности, цилиндра
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
Слайд 8Высота, радиус и ось цилиндра.
Радиусом цилиндра наз. радиус его
основания.
Высотой цилиндра называется расстояние между плоскостями оснований. Высота всегда равна образующей
Высотой цилиндра называется расстояние между плоскостями оснований. Высота всегда равна образующей
Слайд 9Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра, радиус
которого равен 2.
4
Слайд 13Прямая, соединяющая центры оснований цилиндра, называется осью цилиндра.
Сечение цилиндра, проходящее через
ось, называется осевым сечением.
Слайд 17Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это круг,
равный основанию.
Слайд 19Касательная плоскость цилиндра – плоскость проходящая через образующую цилиндра, перпендикулярная осевому
сечению,
проведенному через ту же образующую
Слайд 23Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см)
указаны на рисунке.
Слайд 241) Если дно шляпы опустить на плоскость её полей, то получим
круг радиуса
R = r1+ 10 = 20 cм.
2) Площадь этого круга
3) Найдем площадь боковой поверхности цилиндрической части
4) Найдем площадь шляпы
Ответ: 1600 (см2).
r1=10
10
10
Решение.
Слайд 25Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите:
а) высоту цилиндра; б) So цилиндра
Слайд 26Решение.
1. Проведем диагональ АС сечения АВСD.
A
B
C
D
2. ADC – равнобедренный, прямоугольный, АD=DC,
h = 2r,
CAD = ACD=45, тогда
20
3. Найдем радиус основания
4. Найдем площадь основания
Ответ:
Слайд 27Площадь осевого сечения цилиндра равна 10 м2, а площадь основания –
5 м2. Найдите высоту цилиндра.
Слайд 29Концы отрезка АВ лежат на разных основаниях цилиндра. Радиус цилиндра равен
r, его высота – h, расстояние между прямой АВ и осью цилиндра равно d. Найдите: a) высоту, если r = 10, d = 8, AB = 13.
Слайд 30r
a
Решение.
1. Построим отрезок АВ.
2. Проведем радиус АО.
3. Построим отрезок d.
?
r
d
К
4. Отрезок
ОК – искомое расстояние.
5. Из прямоугольного АОК находим:
С
значит АС = 12.
6. Из прямоугольного АВС находим:
Итак, h = 5.
Ответ: 5.
Слайд 31r
a
r
d
К
С
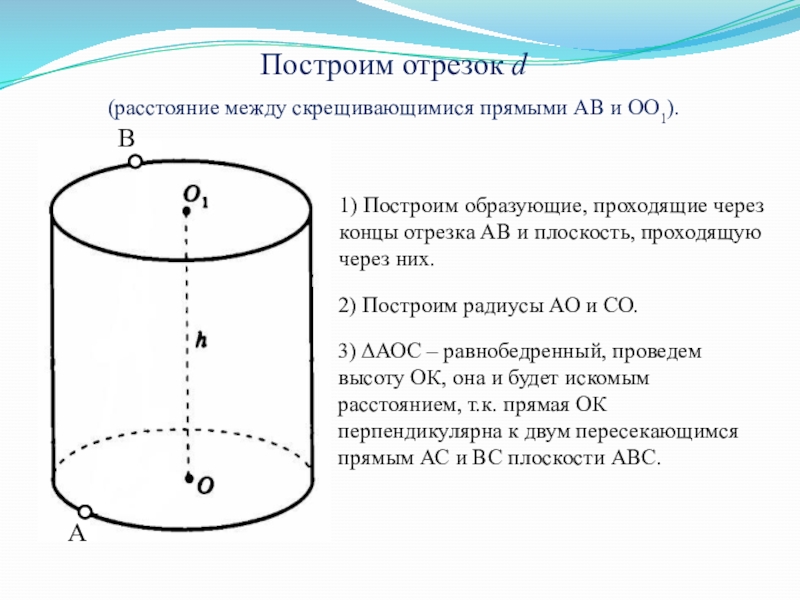
Построим отрезок d
(расстояние между скрещивающимися прямыми АВ и ОО1).
1) Построим
образующие, проходящие через концы отрезка АВ и плоскость, проходящую через них.
2) Построим радиусы АО и СО.
3) АОС – равнобедренный, проведем высоту ОК, она и будет искомым расстоянием, т.к. прямая ОК перпендикулярна к двум пересекающимся прямым АС и ВС плоскости АВС.
Слайд 32Через образующую АА1 цилиндра проведены две секущие плоскости, одна из которых
проходит через ось цилиндра. Найдите отношение площадей сечений цилиндра этими плоскостями, если угол между ними равен .
Слайд 33A
А1
C1
В1
В
C
Решение.
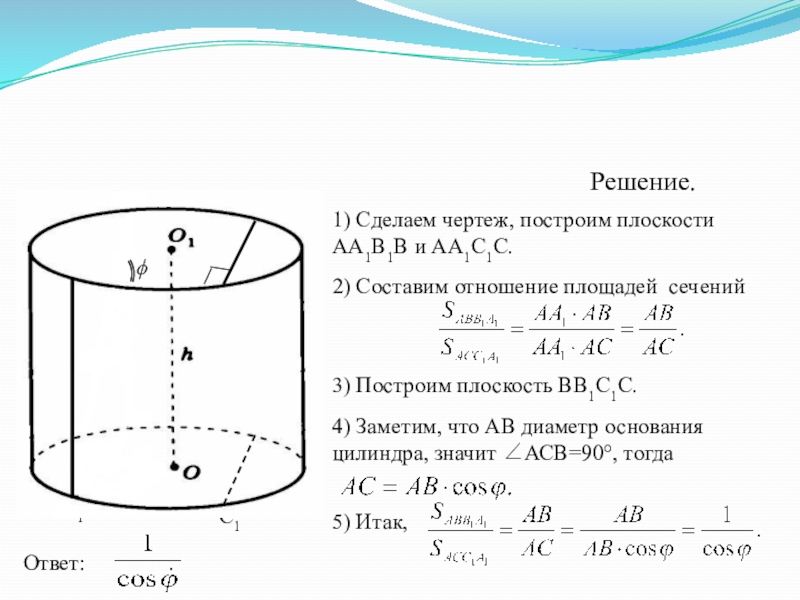
1) Сделаем чертеж, построим плоскости АА1В1В и АА1С1С.
3) Построим плоскость ВВ1С1С.
4)
Заметим, что АВ диаметр основания цилиндра, значит АСВ=90, тогда
2) Составим отношение площадей сечений
5) Итак,
Слайд 34Найти площадь полной поверхности цилиндра
А
В
С
45º
АВС
- прямоугольный
АВС
- равнобедренный
5
ВС=АС=5
r=2,5
S=2π·2,5(5 + 2,5)= 5π·7,5 =
37,5π
АВС
S=2πr(h+r)
АВС
АВС
r
Слайд 35 Площадь осевого сечения цилиндра равна 10 м2, а площадь основания
равна 5 м2. Найдите высоту цилиндра.
Слайд 37 Высота цилиндра равна 8 см, радиус равен 5 см. Найдите
площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3 см.
Слайд 38O
O1
A
B
C
D
K
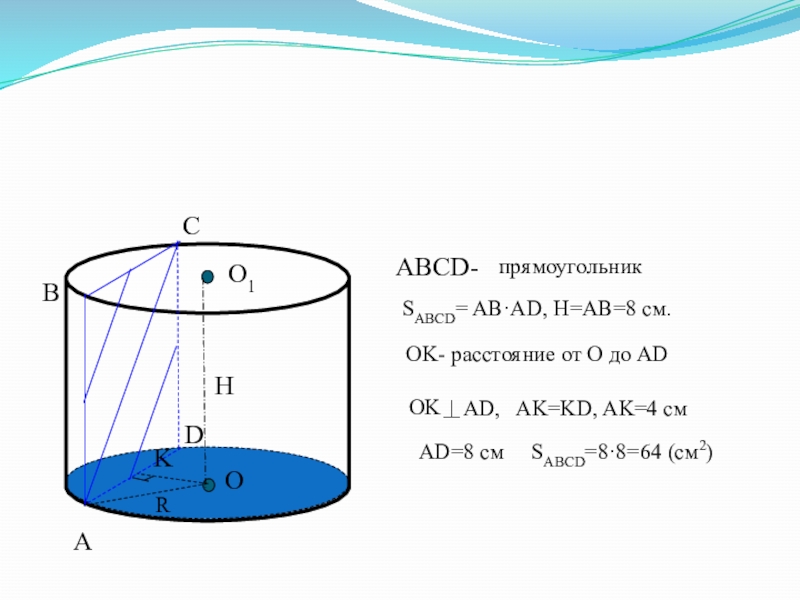
ABCD-
прямоугольник
SABCD= AB·AD, H=AB=8 см.
H
OK- расстояние от О до AD
OK
AD, AK=KD,
AK=4 см
AD=8 см SABCD=8·8=64 (см2)
R
Слайд 40Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его
стороны как оси.
Слайд 41Пусть цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью 3π.
Чему равен радиус цилиндра?
Слайд 42Высота цилиндра 7 см, а радиус основания 5 см. В цилиндре
расположена трапеция так, что все ее вершины находятся на окружностях оснований цилиндра. Найти площадь трапеции и угол между основанием и плоскостью трапеции, если параллельные стороны трапеции равны 6см и 8 см.
Задача.
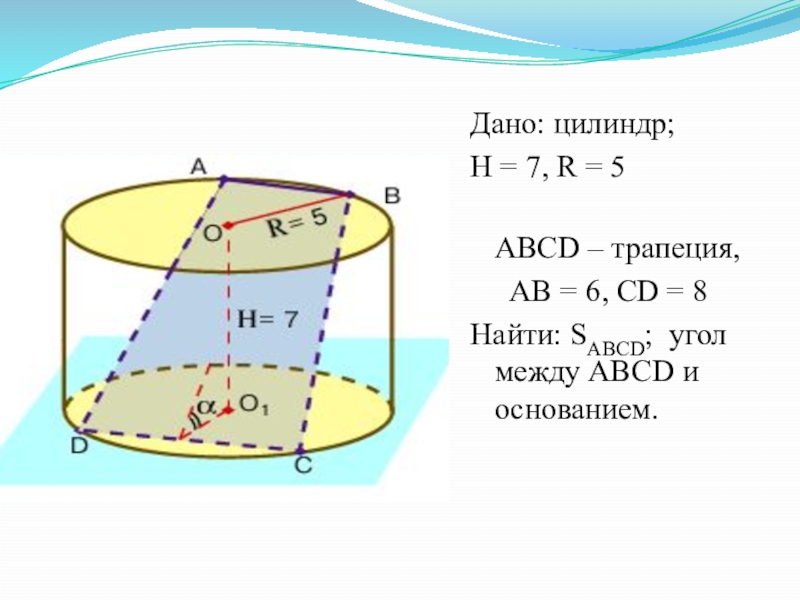
Слайд 43Дано: цилиндр;
Н = 7, R = 5
АВСD – трапеция,
АВ = 6, СD = 8
Найти: SABCD; угол между АВСD и основанием.
Слайд 44Проведем дополнительное построение: построим высоту трапеции, ее проекцию на верхнее основание
цилиндра и перенесем параллельным переносом нижнее основание трапеции на верхнее основание цилиндра.
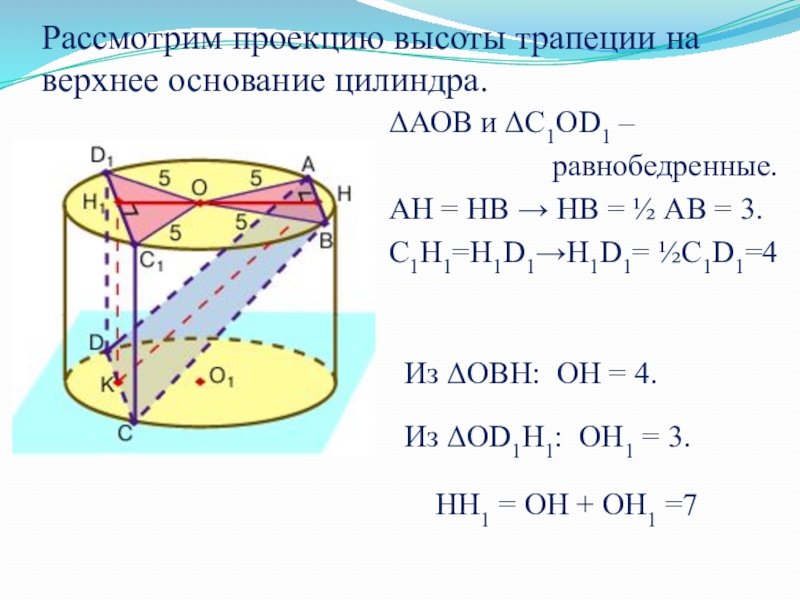
Слайд 46Рассмотрим проекцию высоты трапеции на верхнее основание цилиндра.
ΔАОВ и ΔС1ОD1 –
равнобедренные.
АН = НВ → НВ = ½ АВ = 3.
С1Н1=Н1D1→Н1D1= ½С1D1=4
Из ΔОВН: ОН = 4.
Из ΔОD1Н1: ОН1 = 3.
НН1 = ОН + ОН1 =7
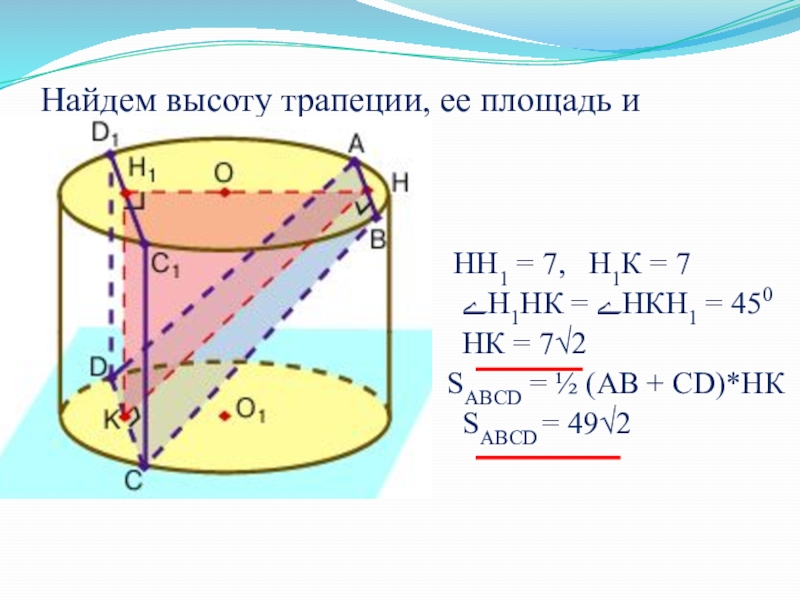
Слайд 47Найдем высоту трапеции, ее площадь и искомый угол.
НН1 = 7,
Н1К = 7
ےН1НК = ےНКН1 = 450
НК = 7√2
SABCD = ½ (АВ + СD)*НК
SАВСD = 49√2
ےН1НК = ےНКН1 = 450
НК = 7√2
SABCD = ½ (АВ + СD)*НК
SАВСD = 49√2
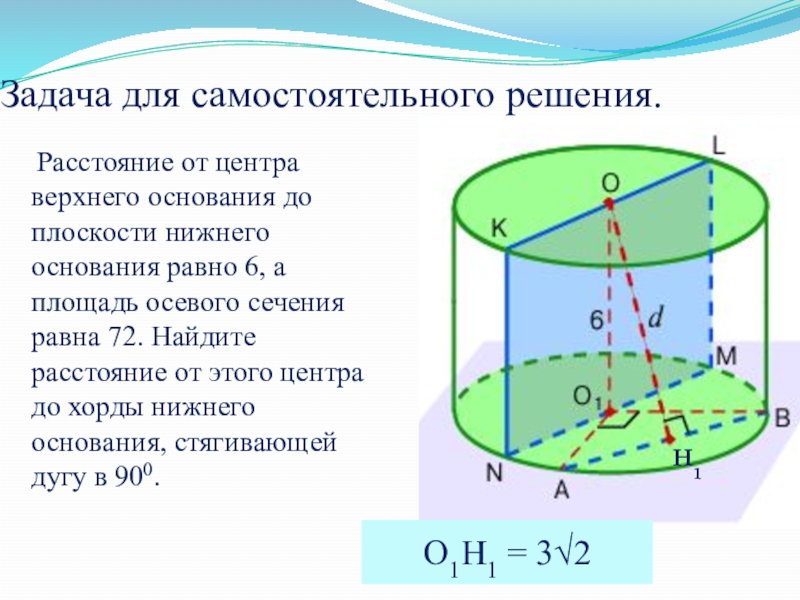
Слайд 48Задача для самостоятельного решения.
Расстояние от центра верхнего основания до
плоскости нижнего основания равно 6, а площадь осевого сечения равна 72. Найдите расстояние от этого центра до хорды нижнего основания, стягивающей дугу в 900.
О1Н1 = 3√2
н1
