- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Цилиндр
Содержание
- 1. Презентация по геометрии на тему Цилиндр
- 2. Содержание Понятие цилиндраСечение цилиндраЦилиндры, окружающие насСложные цилиндрыЗадачиПолучение цилиндраПлощадьПонятие цилиндрической поверхности
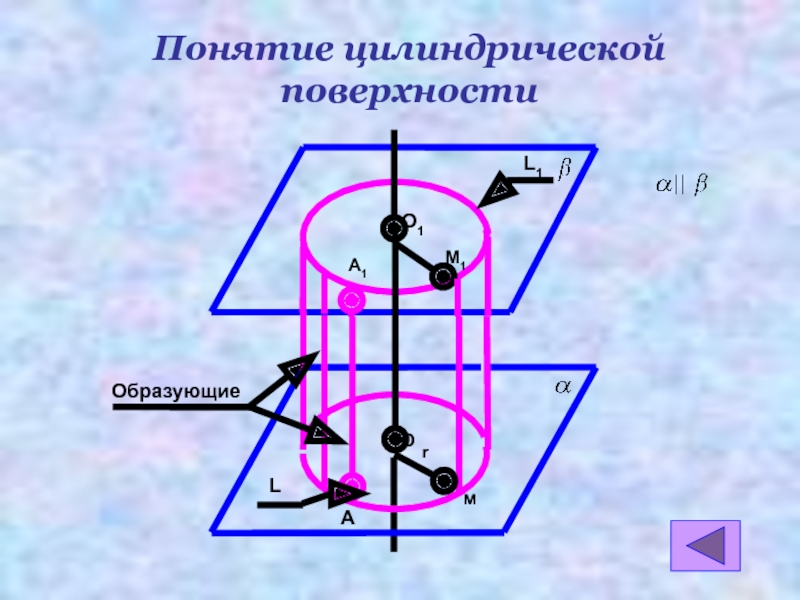
- 3. ОбразующиеA1OO1М1rLмAL1Понятие цилиндрической поверхности||
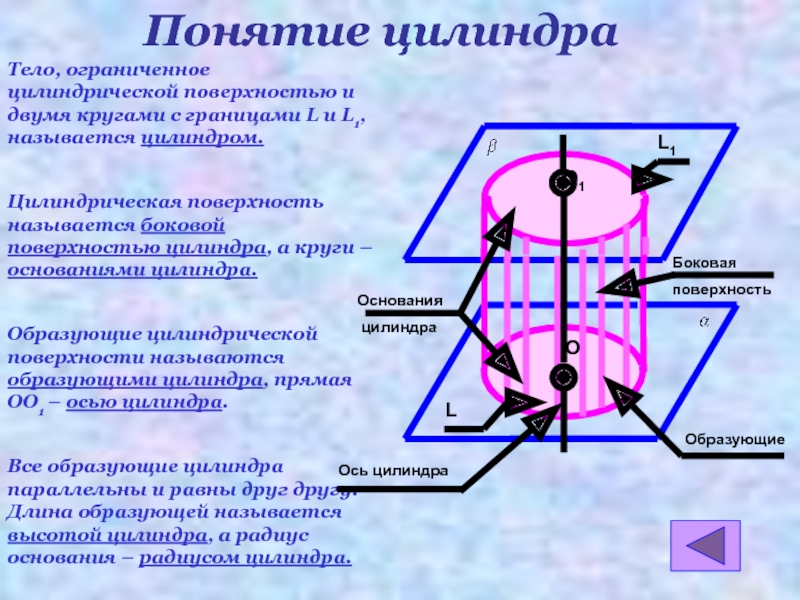
- 4. Тело, ограниченное цилиндрической поверхностью и двумя кругами
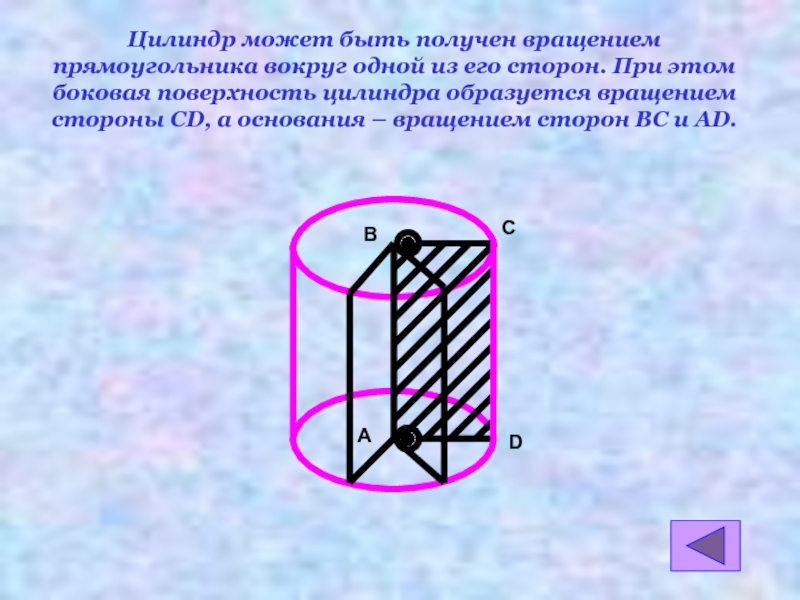
- 5. Цилиндр может быть получен вращением прямоугольника вокруг
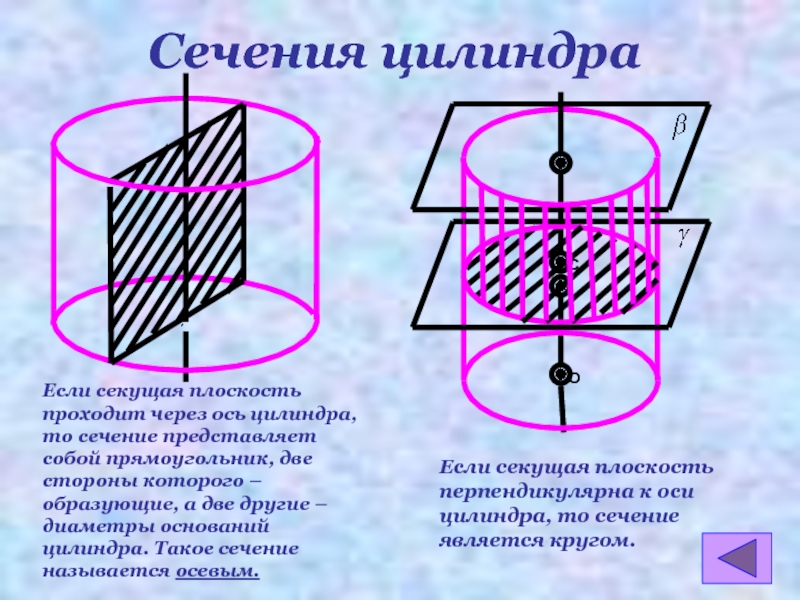
- 6. Сечения цилиндраЕсли секущая плоскость проходит через ось
- 7. Предметы, окружающей обстановки, дающие представление о цилиндре.
- 8. Например, цилиндр, каждое основание которого представляет собой
- 9. Площадь поверхности цилиндра За площадь боковой поверхности
- 10. Задачи IНайдите:а) h;б) r ;в) Sосн.II
- 11. IIIДано: h=8см, r=5см, АВСD- сечение, (АВС) ||
- 12. Материал подготовила: Морозова Т.Л.
Содержание Понятие цилиндраСечение цилиндраЦилиндры, окружающие насСложные цилиндрыЗадачиПолучение цилиндраПлощадьПонятие цилиндрической поверхности
Слайд 2
Содержание
Понятие цилиндра
Сечение цилиндра
Цилиндры, окружающие нас
Сложные цилиндры
Задачи
Получение цилиндра
Площадь
Понятие цилиндрической поверхности
Слайд 4Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и
L1, называется цилиндром.
Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, прямая ОО1 – осью цилиндра.
Все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, прямая ОО1 – осью цилиндра.
Все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Боковая
поверхность
Образующие
Ось цилиндра
Понятие цилиндра
Основания
цилиндра
О
О1
L
L1
Слайд 5Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.
При этом боковая поверхность цилиндра образуется вращением стороны СD, а основания – вращением сторон ВС и АD.
D
А
В
С
Слайд 6
Сечения цилиндра
Если секущая плоскость проходит через ось цилиндра, то сечение представляет
собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.
С
О
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.
Слайд 8Например, цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы
и отрезком или цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований.
На практике нередко встречаются предметы, которые имеют форму более сложных цилиндров.
Слайд 9
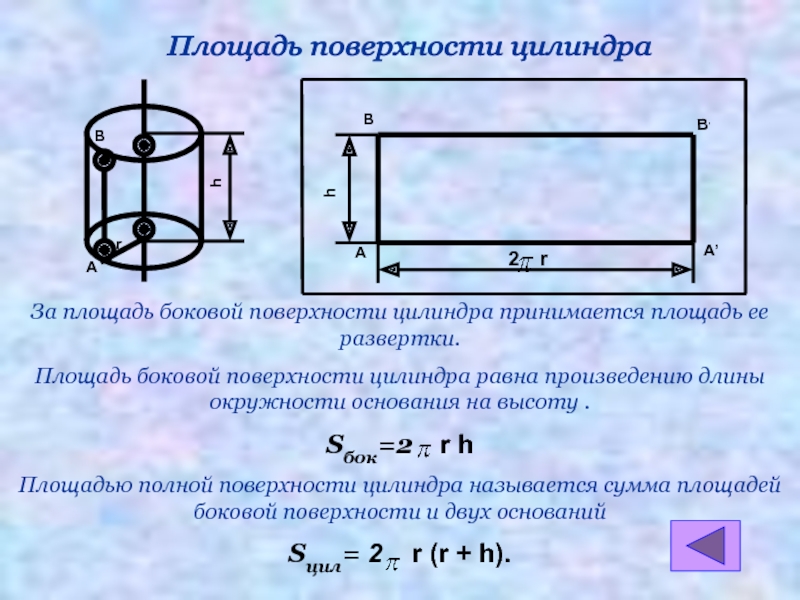
Площадь поверхности цилиндра
За площадь боковой поверхности цилиндра принимается площадь ее
развертки.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту .
Sбок=2 r h
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований
Sцил= 2 r (r + h).
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту .
Sбок=2 r h
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований
Sцил= 2 r (r + h).
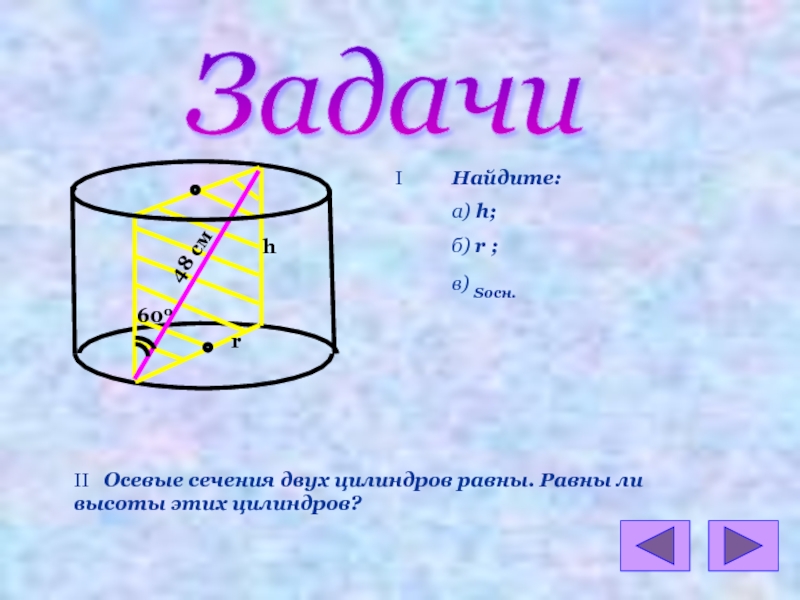
Слайд 10Задачи
I
Найдите:
а) h;
б) r ;
в) Sосн.
II Осевые сечения двух цилиндров
равны. Равны ли высоты этих цилиндров?
Слайд 11
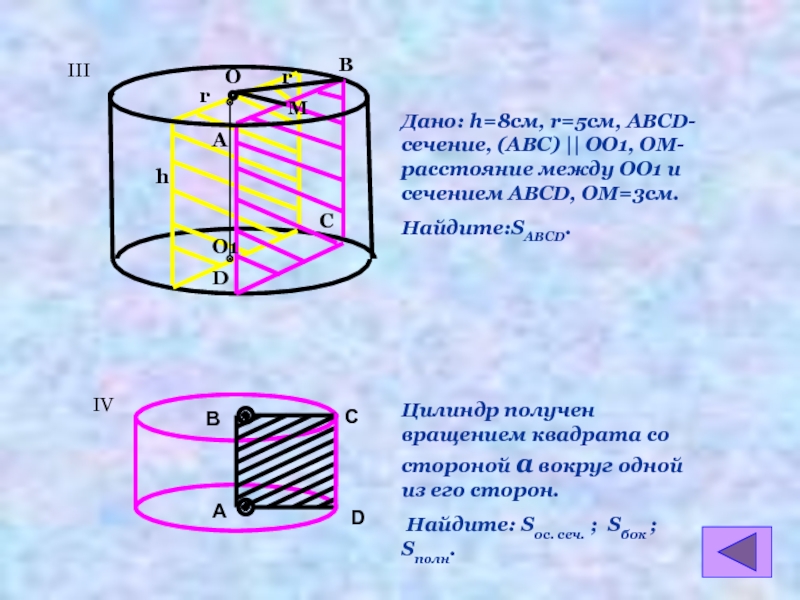
III
Дано: h=8см, r=5см, АВСD- сечение, (АВС) || ОО1, ОМ-расстояние между ОО1
и сечением АВСD, ОМ=3см.
Найдите:SАВСD.
Найдите:SАВСD.
IV
D
Цилиндр получен вращением квадрата со стороной а вокруг одной из его сторон.
Найдите: Sос. сеч. ; Sбок ; Sполн.
