- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Цилиндр
Содержание
- 1. Презентация по геометрии на тему Цилиндр
- 2. Содержание.Основные понятия.Сечения.Примечания.Развертка боковой поверхности цилиндра.Площадь поверхности цилиндра.Где встречается цилиндр.
- 3. Основные понятия.Тело, ограниченное цилиндрической поверхностью и двумя
- 4. Слайд 4
- 5. Цилиндр может быть получен вращением прямоугольника вокруг
- 6. Сечения.Если секущая плоскость проходит через ось цилиндра,
- 7. Если секущая плоскость перпендикулярна к оси цилиндра,
- 8. Примечания.На практике нередко встречаются предметы, которые имеют
- 9. На данном рисунке изображен цилиндр, основаниями которого
- 10. Развертка боковой поверхности цилиндра.Представим себе, что его
- 11. Основание АА1 прямоугольника является разверткой окружности основания
- 12. Где встречается цилиндр.
Содержание.Основные понятия.Сечения.Примечания.Развертка боковой поверхности цилиндра.Площадь поверхности цилиндра.Где встречается цилиндр.
Слайд 2Содержание.
Основные понятия.
Сечения.
Примечания.
Развертка боковой поверхности цилиндра.
Площадь поверхности цилиндра.
Где встречается цилиндр.
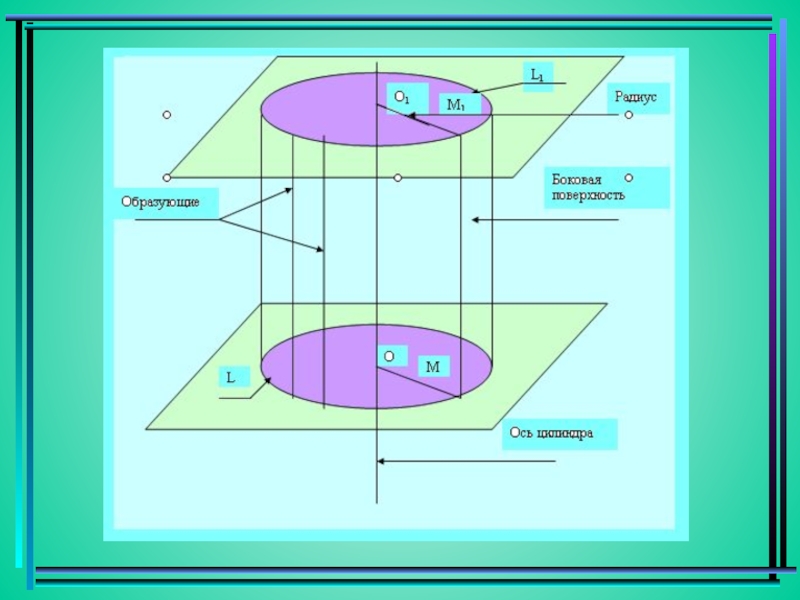
Слайд 3Основные понятия.
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L
и L1, называется цилиндром.
Цилиндрическая поверхность называется боковой поверхностью цилиндра.
Круги – основания цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра. (Все образующие равны)
Прямая ОО1 – ось цилиндра.
Длина образующей называется высотой цилиндра.
Радиус основания является радиусом цилиндра.
Цилиндрическая поверхность называется боковой поверхностью цилиндра.
Круги – основания цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра. (Все образующие равны)
Прямая ОО1 – ось цилиндра.
Длина образующей называется высотой цилиндра.
Радиус основания является радиусом цилиндра.
Слайд 5Цилиндр может быть получен вращением прямоугольника вокруг одной его из его
сторон.
Боковая поверхность образуется вращением стороны СD, а основания – вращением сторон AD и BC.
Боковая поверхность образуется вращением стороны СD, а основания – вращением сторон AD и BC.
Слайд 6Сечения.
Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой
прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называют осевым.
Слайд 7Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.
Плоскость отсекает от рассматриваемого цилиндра тело, также представляющее собой цилиндр. Основаниями этого цилиндра служат два круга, один из которых и есть рассматриваемое сечение.
Слайд 8Примечания.
На практике нередко встречаются предметы, которые имеют форму более сложных цилиндров.
На
этом рисунке изображен цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком.
Слайд 9На данном рисунке изображен цилиндр, основаниями которого являются круги , но
образующие цилиндра не перпендикулярны к плоскостям оснований. Такой цилиндр называется наклонным цилиндром.
Слайд 10Развертка боковой поверхности цилиндра.
Представим себе, что его боковую поверхность разрезали по
образующей АВ и развернули таким образом, что все образующие оказались в одной плоскости.
Полученный прямоугольник называется разверткой боковой поверхности цилиндра.
Полученный прямоугольник называется разверткой боковой поверхности цилиндра.
Слайд 11Основание АА1 прямоугольника является разверткой окружности основания цилиндра, а высота –
образующей цилиндра, поэтому АА1 = 2Пr, АВ = h.
За площадь боковой поверхности цилиндра принимается площадь ее развертки.
Sбок = 2Пrh.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
Sпол = 2Пrh + 2Пr 2 = 2Пr (r + h)
За площадь боковой поверхности цилиндра принимается площадь ее развертки.
Sбок = 2Пrh.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
Sпол = 2Пrh + 2Пr 2 = 2Пr (r + h)
Площадь поверхности цилиндра.