- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Цилиндр, конус, шар
Содержание
- 1. Презентация по геометрии на тему Цилиндр, конус, шар
- 2. ПОНЯТИЕ ЦИЛИНДРА
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Цилиндр – это тело, ограниченное цилиндрической поверхностью
- 8. цилиндрической поверхностью называется множество отрезков, соединяющих точки двух окружностей, находящихся в параллельных плоскостях
- 9. Площадь боковой поверхности цилиндраААВВhrS =2 hБоковая поверхность
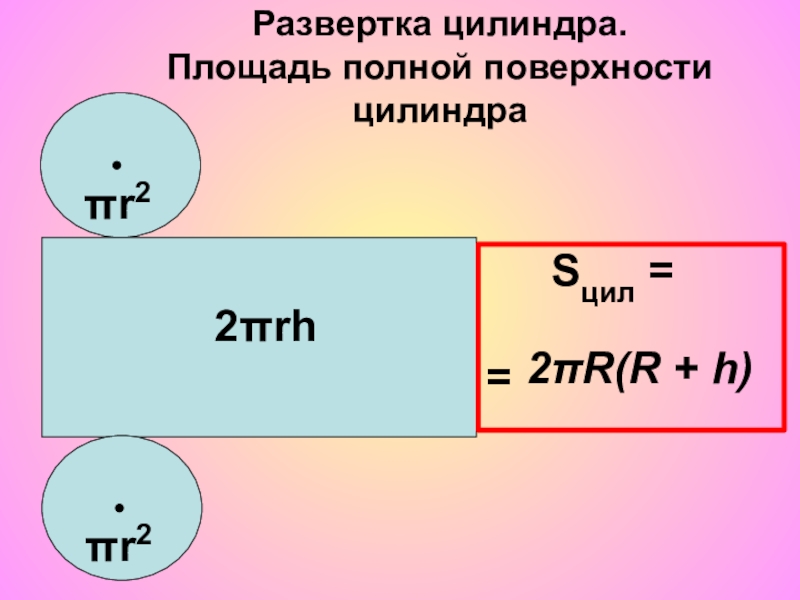
- 10. Развертка цилиндра. Площадь полной поверхности цилиндраSцил = =πr2πr22πrh2πR(R + h)
- 11. Сечения цилиндра Осевое сечение - прямоугольникОО
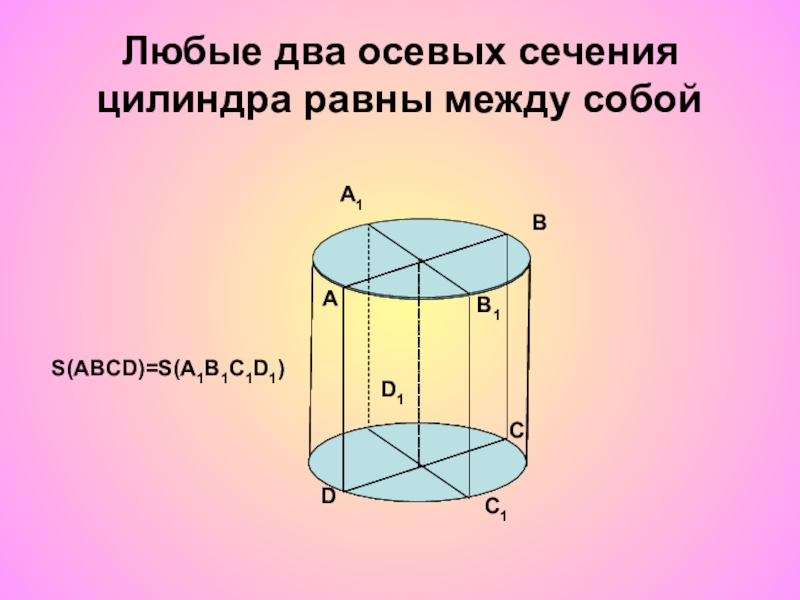
- 12. Любые два осевых сечения цилиндра равны между собойABCDA1B1C1D1S(ABCD)=S(A1B1C1D1)
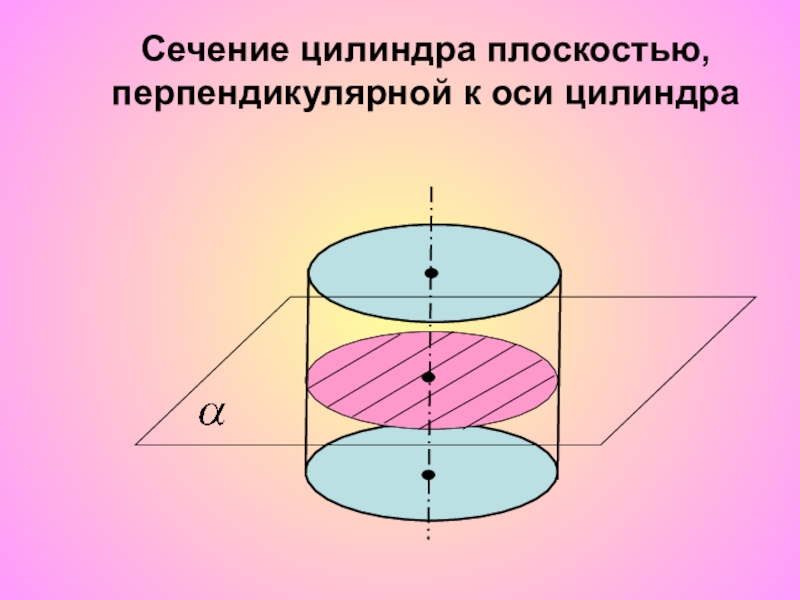
- 13. Сечение цилиндра плоскостью, перпендикулярной к оси цилиндра
- 14. Сечения, параллельные оси цилиндра - прямоугольники
- 15. Слайд 15
- 16. Решение задачЗадача 1. Радиус основания цилиндра 2
- 17. № 522. Диагональ осевого сечения цилиндра равна
- 18. Равносторонний цилиндрHRH = 2R
- 19. Найти площадь полной поверхности цилиндраАВС45ºАВС- прямоугольныйАВС- равнобедренный5ВС=АС=5r=2,5S=2π·2,5(5 + 2,5)= 5π·7,5 = 37,5πАВСS=2πr(h+r)АВСАВСr
- 20. Площадь осевого сечения цилиндра равна 10
- 21. Высота цилиндра равна 8 см, радиус
- 22. Осевое сечение цилиндра – квадрат, диагональ которого
- 23. Какая фигура получается в сечении цилиндра
- 24. Площадь боковой поверхности конуса
- 25. Объем конуса Теорема: Объем конуса равен однойтрети произведения площадиоснования на высоту.
- 26. Объём усеченного конуса Следствие: Объем усеченногоконуса, высота
- 27. Сечение конуса различными плоскостями.а) секущая плоскость проходит
- 28. Вокруг нас…Детская пирамидка в
- 29. Форма конуса в природеЕльПихтаКипарисыСилуэт горы БелухаСилуэт горы Броуд Пик
- 30. Конус. Площадь поверхности конуса
- 31. Из предложенных геометрических фигур выбрать конус
- 32. Коническая поверхность
- 33. Коническая поверхность
- 34. Тело, ограниченное конической поверхностью
- 35. Конус – тело вращения… Конус
- 36. S - вершина конусаSA, SB – образующиеSO
- 37. Слайд 37
- 38. Слайд 38
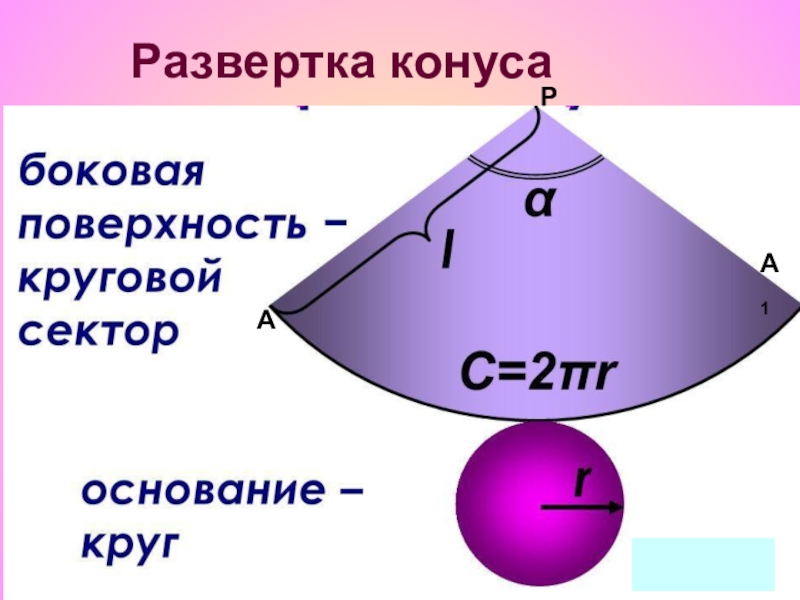
- 39. АА1РРазвертка конуса
- 40. Площадь поверхности конуса
- 41. Усеченный конус
- 42. Возьмём произвольный конус и проведём секущую плоскость,
- 43. Основание исходного конуса и круг, полученный в
- 44. Часть конической поверхности, ограничивающая усечённый конус, называется
- 45. Усечённый конус может быть получен вращением прямоугольной
- 46. Площадь боковой поверхности усечённого конуса равна произведению
- 47. Площадь полной поверхности усечённого конусаПолная площадь поверхности
- 48. ЗАДАЧА 1.По данным чертежа
- 49. ЗАДАЧА 1Дано: конус; R=3,l=5.Найти: SБПК , Sппк.Решение.SБПК = π*3*5=15 π;Sосн = π*32 =9 π;Sппк =15π+9π=24π.ОАВК35О
- 50. ЗАДАЧА 2.По данным чертежа
- 51. ЗАДАЧА 2.Дано: конус; R=5, h=12.Найти: SБПК ,
- 52. ЗАДАЧА 3.По данным чертежа
- 53. ЗАДАЧА 3.Дано: конус; R=6,∟АКО=30о.Найти: SБПК , Sппк.Решение.l=R/sin30о,l=6/0.5=12;SБПК=π*12*6=72π;Sосн = π*62 =36π;Sппк =72π+36π; Sппк =108π.30оКАВО6
- 54. ЗАДАЧА 4.РАВНЫ ЛИ ПЛОЩАДИ ПОВЕРХНОСТЕЙ ДВУХ КОНУСОВ,
- 55. РЕШЕНИЕ ЗАДАЧИ 41) R=ВС= a ;
- 56. Сфера .
- 57. Определение сферы!Сферой называется поверхность, состоящая из всех
- 58. Площадь сферы и шараСферу нельзя развернуть на
- 59. Задача 2 Найти площадь поверхности сферы,
- 60. Задача 3Найти площадь поверхности шара, площадь центрального
- 61. O№ 4 Вершины треугольника АВС лежат на
- 62. ODNBPAO1CDAB№ 5 Все стороны ромба, диагонали которого
- 63. Объемы тел вращения
- 64. Объем цилиндраV = Sосн·HSосн = πR 2
- 65. Объем конуса. V = 1/3Sосн·H Sосн = πR 2
- 66. Объем усеченного конуса.V=⅓πh(R +R R +R )211222hR1R2
- 67. Объем шара.V = 4/3πR3
- 68. ЗадачаБоковые ребра правильной треугольной пирамиды составляют с
- 69. ЗадачаДлина окружности сечения шара плоскостью, равна 12π
- 70. ЗадачаПлощадь сечения шара плоскостью, проведенной на расстоянии
- 71. Осевое сечение конуса – равносторонний треугольник, периметр которого равен 12√3 см. Вычислить объем конуса.
- 72. . Осевое сечение цилиндра плоскостью – квадрат, площадь которого равна 36 см . Найдите объем цилиндра.2
- 73. Длина окружности сечения шара плоскостью равна
- 74. УСПЕХОВ!
Слайд 1Цилиндр, конус, шар
ГБПОУ СО «Свердловский областной педагогический колледж»
Преподаватель Перминова Е.В.
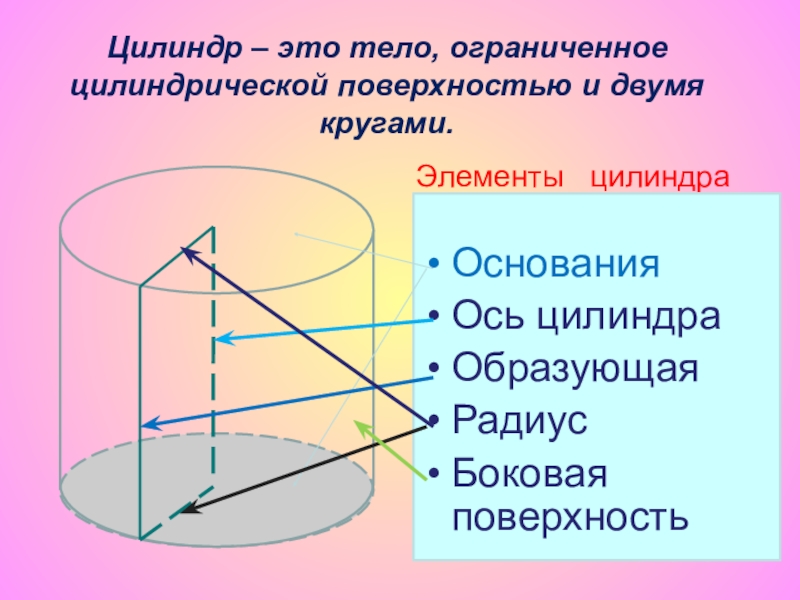
Слайд 7Цилиндр – это тело, ограниченное цилиндрической поверхностью и двумя кругами.
Основания
Ось цилиндра
Образующая
Радиус
Боковая поверхность
Слайд 8цилиндрической поверхностью называется множество отрезков, соединяющих точки двух окружностей, находящихся в
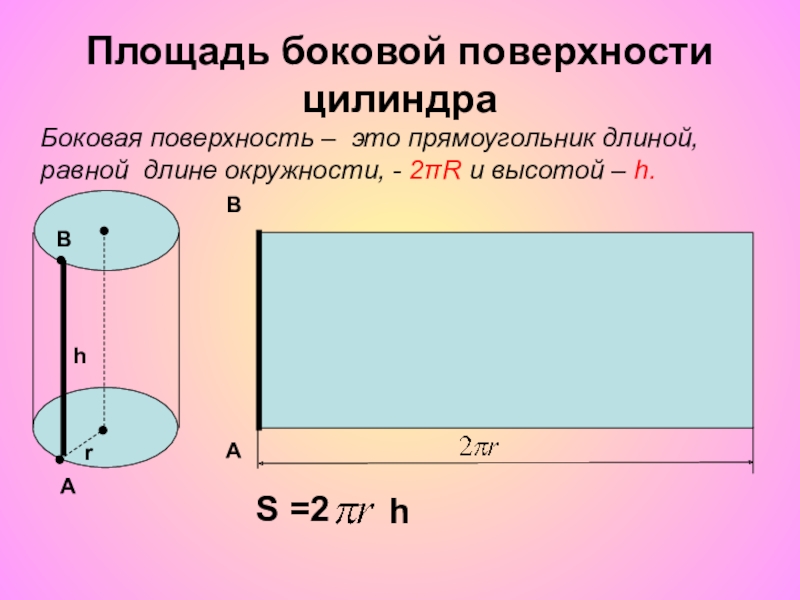
Слайд 9Площадь боковой поверхности цилиндра
А
А
В
В
h
r
S =2
h
Боковая поверхность – это прямоугольник длиной,
Слайд 16Решение задач
Задача 1. Радиус основания цилиндра 2 м, а высота 3
Дано: цилиндр,
АВСD -
В О С R = . . . . . = 2 м
H = . . . . . = 3 м
АС -
Найти: АС.
А О1 D
Решение.
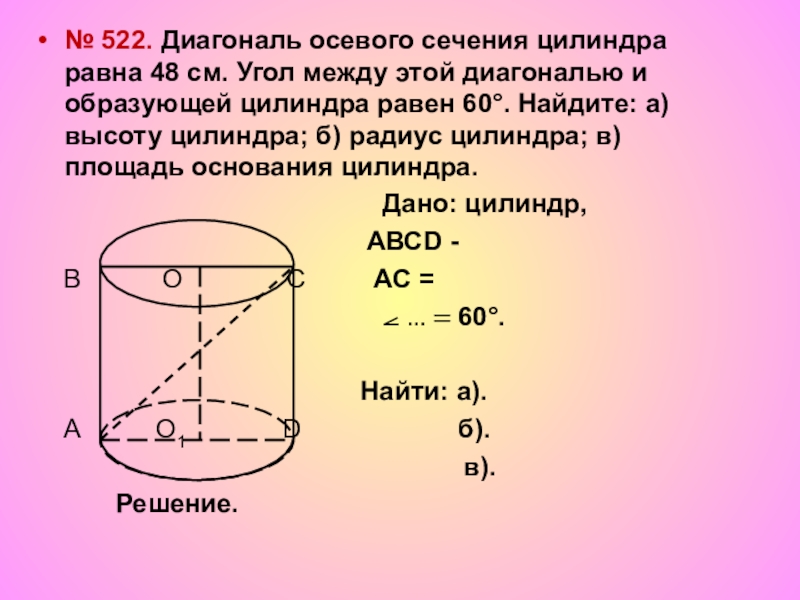
Слайд 17№ 522. Диагональ осевого сечения цилиндра равна 48 см. Угол между
Дано: цилиндр,
АВСD -
В О С АС =
⦟ … = 60°.
Найти: а).
А О1 D б).
в).
Решение.
Слайд 19Найти площадь полной поверхности цилиндра
А
В
С
45º
АВС
- прямоугольный
АВС
- равнобедренный
5
ВС=АС=5
r=2,5
S=2π·2,5(5 + 2,5)= 5π·7,5 =
АВС
S=2πr(h+r)
АВС
АВС
r
Слайд 20 Площадь осевого сечения цилиндра равна 10 м2, а площадь основания
А
В
С
D
O
O1
R
H
R=
H=
м
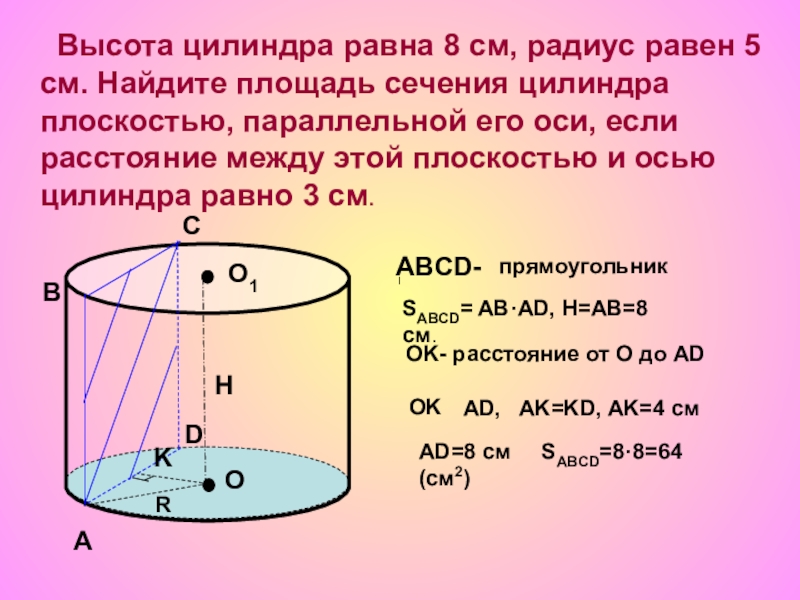
Слайд 21 Высота цилиндра равна 8 см, радиус равен 5 см. Найдите
O
O1
A
B
C
D
K
ABCD-
прямоугольник
SABCD= AB·AD, H=AB=8 см.
H
OK- расстояние от О до AD
OK
AD, AK=KD, AK=4 см
AD=8 см SABCD=8·8=64 (см2)
R
Слайд 22Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см.
Найдите: а)
О
О1
А
В
С
D
ABCD-квадрат
Н=СD, CD=AD
2CD2=AC2
CD=10
см
R=0,5AD=5
см
S=50
см2
Слайд 23Какая фигура получается в сечении цилиндра
плоскостью, проходящей перпендикулярно оси
цилиндра?
Круг
Какая фигура
Прямоугольник
Чему равна площадь осевого сечения
равностороннего цилиндра, высота
которого равна 6 см?
36 см2
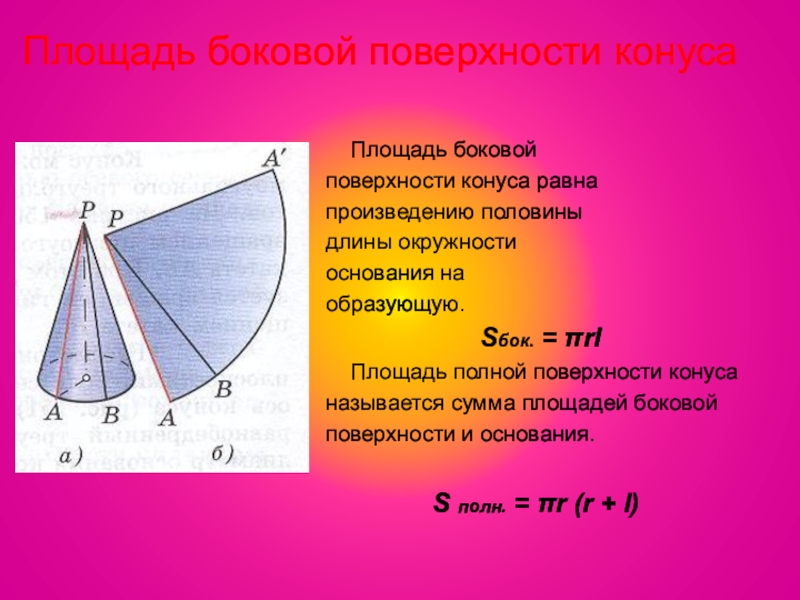
Слайд 24Площадь боковой поверхности конуса
Площадь боковой
поверхности конуса
произведению половины
длины окружности
основания на
образующую.
Sбок. = πrl
Площадь полной поверхности конуса
называется сумма площадей боковой
поверхности и основания.
S полн. = πr (r + l)
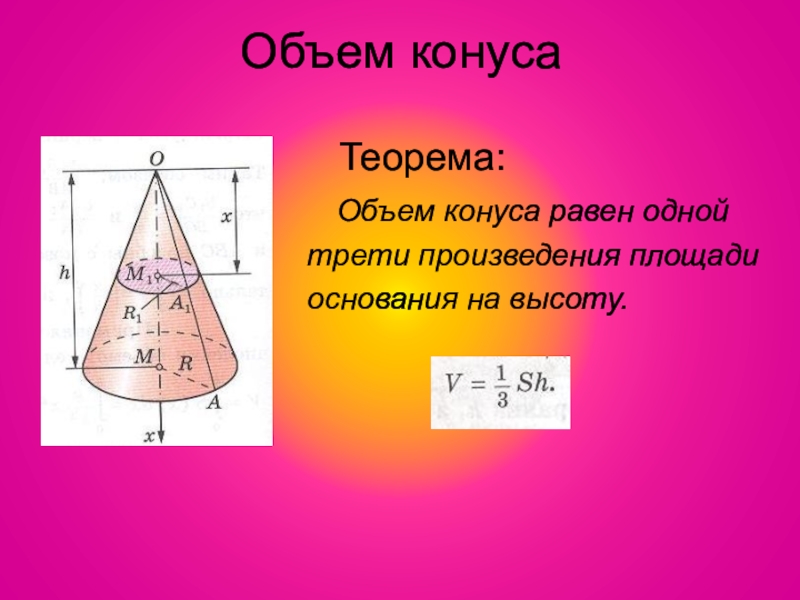
Слайд 25Объем конуса
Теорема:
Объем конуса равен одной
трети произведения площади
основания
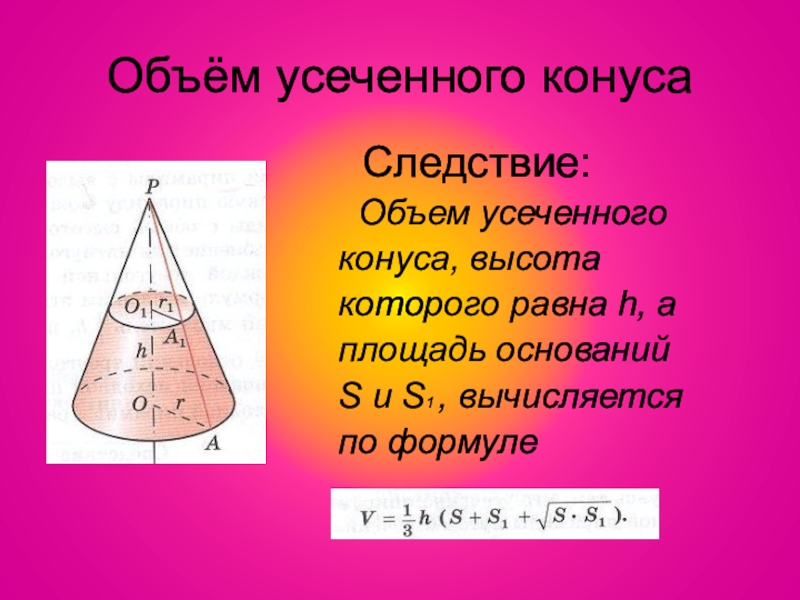
Слайд 26Объём усеченного конуса
Следствие:
Объем усеченного
конуса, высота
которого равна h, а
площадь
S и S1 , вычисляется
по формуле
Слайд 27Сечение конуса различными плоскостями.
а) секущая плоскость проходит через ось конуса, осевое
б) секущая плоскость проходит перпендикулярно к оси конуса, сечением является круг.
в) сечение, пересекающее только одну часть кругового конуса и не параллельное ни одной его образующей – эллипс.
а)
б)
в)
Слайд 28Вокруг нас…
Детская пирамидка в
виде конуса
Силуэт летящей кометы
Форма вафельного
рожка для мороженного
Дорожные конусы
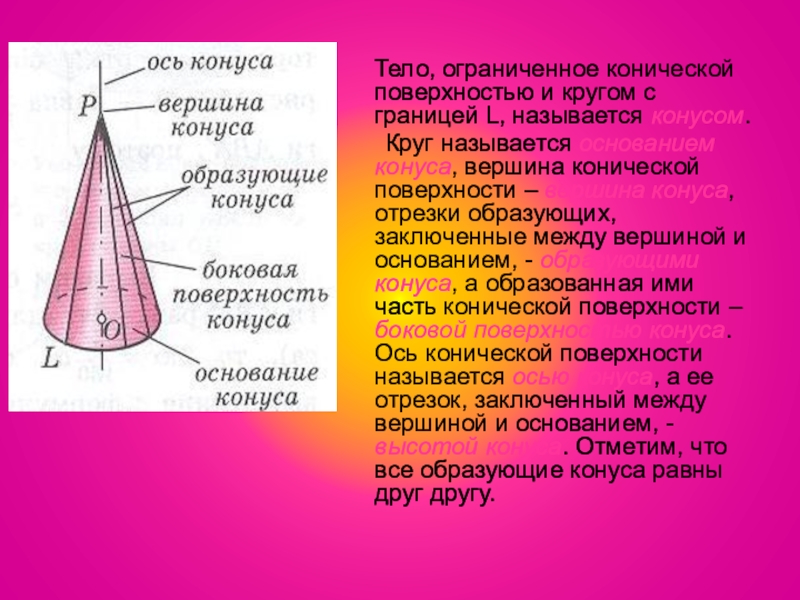
Слайд 34 Тело, ограниченное конической поверхностью и кругом с границей
Круг называется основанием конуса, вершина конической поверхности – вершина конуса, отрезки образующих, заключенные между вершиной и основанием, - образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Ось конической поверхности называется осью конуса, а ее отрезок, заключенный между вершиной и основанием, - высотой конуса. Отметим, что все образующие конуса равны друг другу.
Слайд 35Конус – тело вращения…
Конус можно получить путем вращения
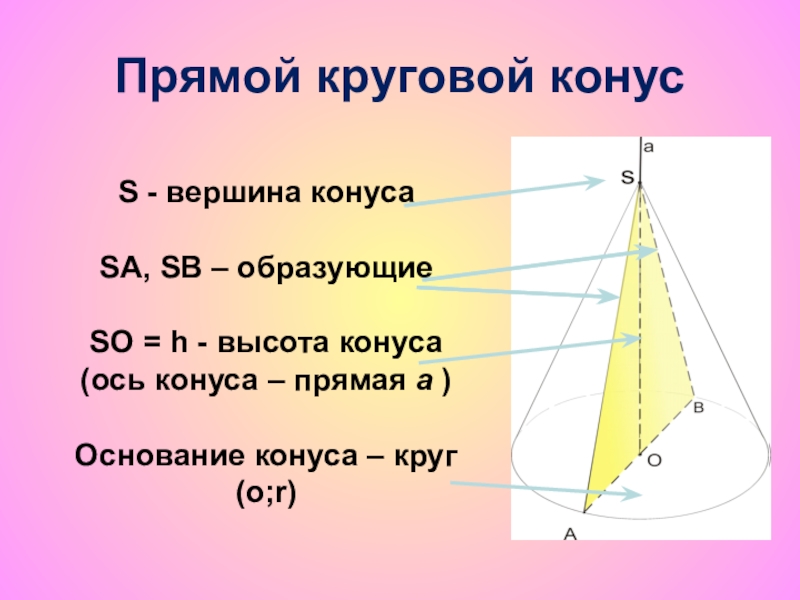
Слайд 36S - вершина конуса
SA, SB – образующие
SO = h - высота
(ось конуса – прямая а )
Основание конуса – круг (о;r)
Прямой круговой конус
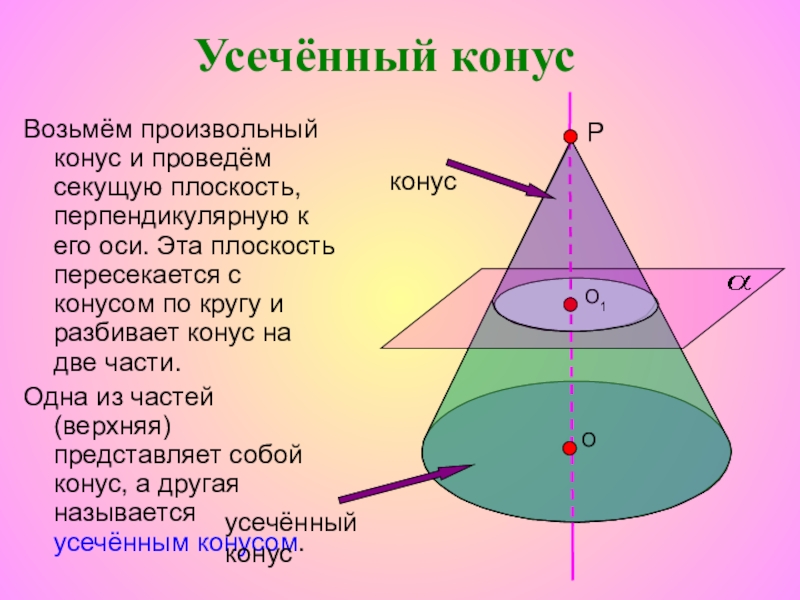
Слайд 42Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси.
Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом.
Усечённый конус
Р
О
О1
конус
усечённый конус
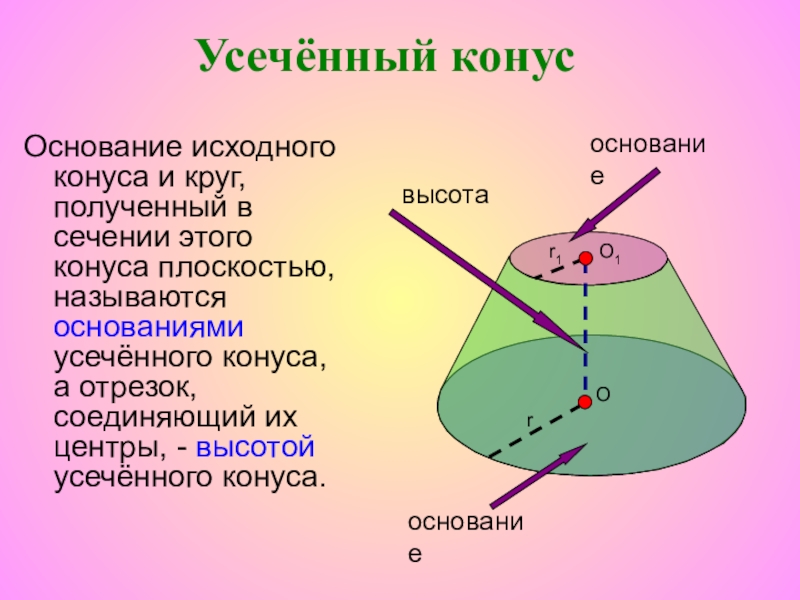
Слайд 43Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью,
Усечённый конус
О1
r1
r
О
основание
основание
высота
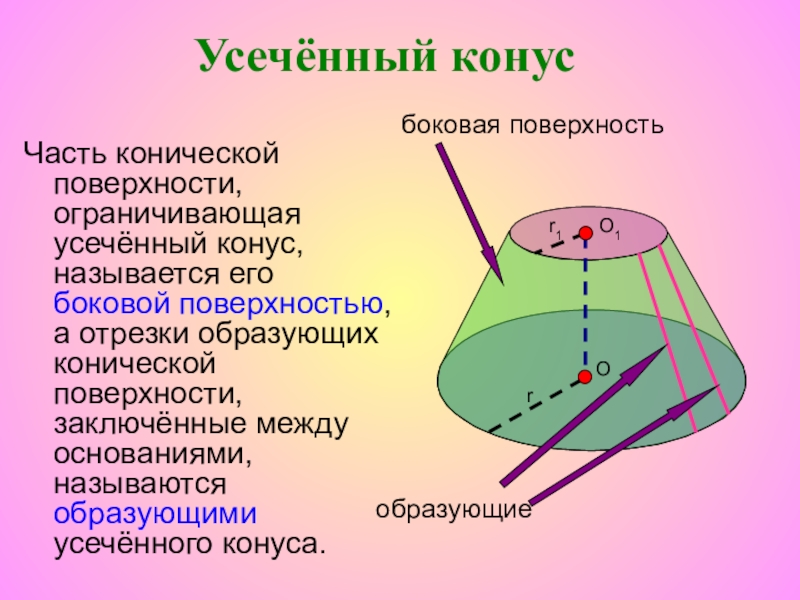
Слайд 44Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а
Усечённый конус
О1
r1
r
О
боковая поверхность
образующие
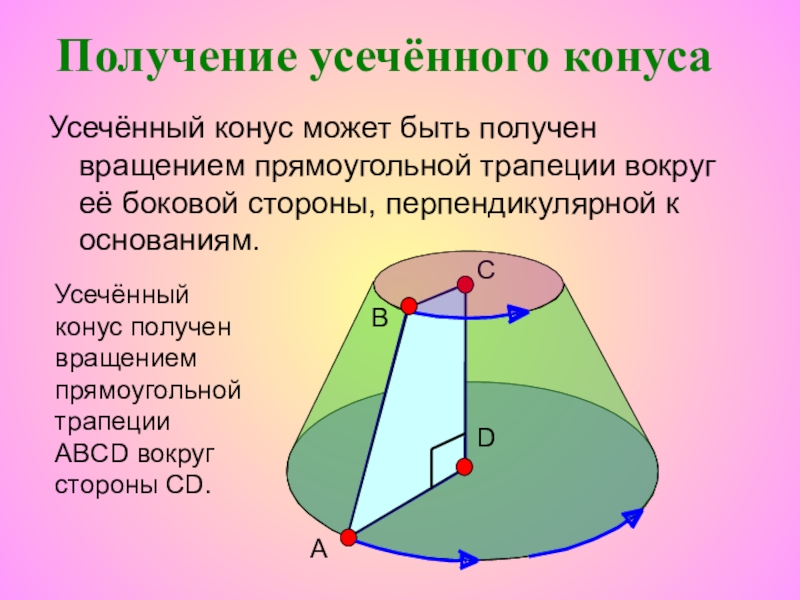
Слайд 45Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой
Получение усечённого конуса
A
B
C
D
Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.
Слайд 46Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований
где r и r1 – радиусы оснований, L – образующая усечённого конуса.
Площадь боковой поверхности усечённого конуса
О1
r1
r
О
L
Слайд 47Площадь полной поверхности усечённого конуса
Полная площадь поверхности усеченного конуса равна сумме площадей
Основания усеченного конуса есть круги и их площадь вычисляется по формуле площади круга:
S=π (r12+(r1+ r2) l+ r22)
Слайд 48ЗАДАЧА 1.
По данным чертежа (ОВ=3, КВ=5) вычислите
О
А
В
К
3
5
О
Слайд 49ЗАДАЧА 1
Дано: конус; R=3,l=5.
Найти: SБПК , Sппк.
Решение.
SБПК = π*3*5=15 π;
Sосн =
Sппк =15π+9π=24π.
О
А
В
К
3
5
О
Слайд 50ЗАДАЧА 2.
По данным чертежа (ОВ=5, КО=12) вычислите площадь
А
О
В
К
5
12
Слайд 51ЗАДАЧА 2.
Дано: конус; R=5, h=12.
Найти: SБПК , Sппк.
Решение.
l2=144+25=169, l=13;
SБПК=π*13*5=65 π;
Sосн =
Sппк =65π+25π;
Sппк =90π.
О
В
К
5
12
А
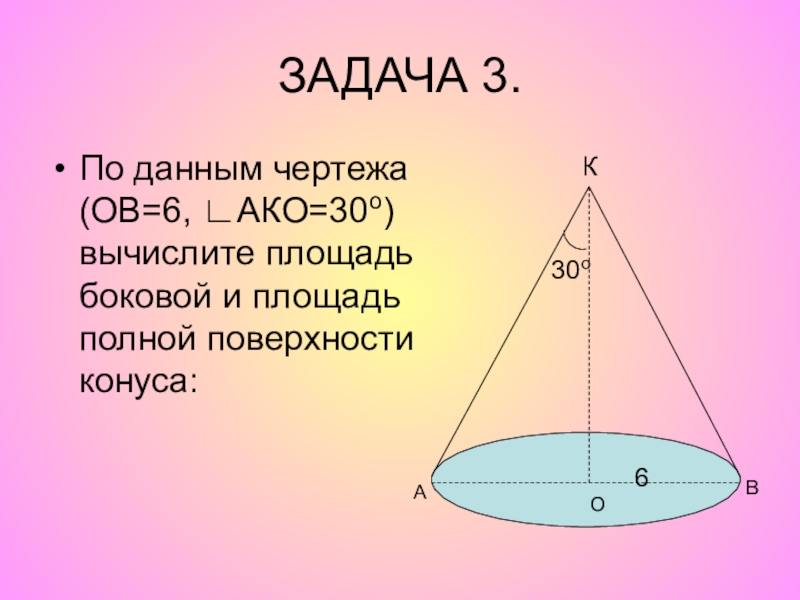
Слайд 52ЗАДАЧА 3.
По данным чертежа (ОВ=6, ∟АКО=30о) вычислите площадь
30о
К
А
В
О
6
Слайд 53ЗАДАЧА 3.
Дано: конус; R=6,∟АКО=30о.
Найти: SБПК , Sппк.
Решение.
l=R/sin30о,l=6/0.5=12;
SБПК=π*12*6=72π;
Sосн = π*62 =36π;
Sппк =72π+36π;
Sппк =108π.
30о
К
А
В
О
6
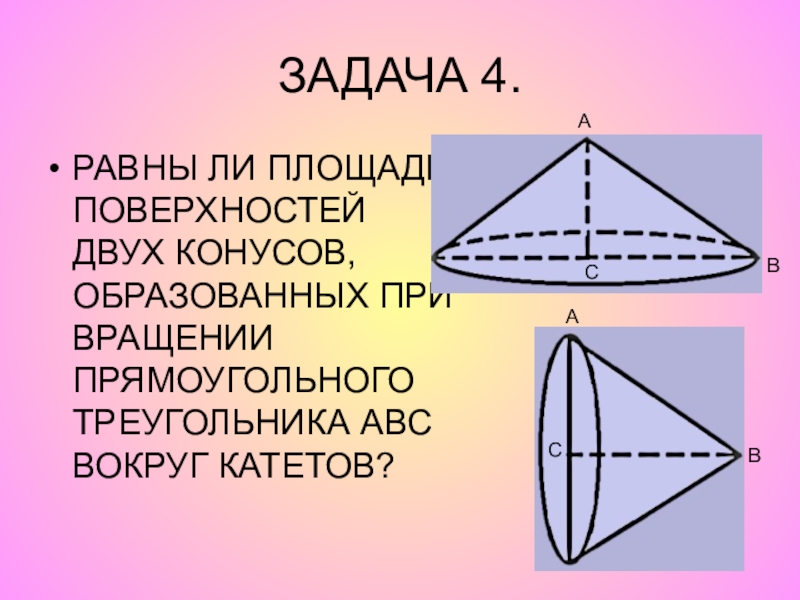
Слайд 54ЗАДАЧА 4.
РАВНЫ ЛИ ПЛОЩАДИ ПОВЕРХНОСТЕЙ ДВУХ КОНУСОВ, ОБРАЗОВАННЫХ ПРИ ВРАЩЕНИИ ПРЯМОУГОЛЬНОГО
А
С
А
В
С
С
В
С
Слайд 55РЕШЕНИЕ ЗАДАЧИ 4
1) R=ВС= a ;
2) R=АС= b ; SППК 2= SБПК 2+ Sосн2=π b с+π b2= π b (b + с).
Если SППК 1 = SППК 2, то a2 +aс = b2 +bc, a2-b2+ac - bc=0, (a-b)(a+b+c)=0. Т.к a,b,c – положительные числа (длины сторон треугольника), то равенство верно только в случае, если a = b.
Слайд 57Определение сферы!
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на
d
О
R – радиус сферы – отрезок,
соединяющий любую точку
сферы с центром.
d – диаметр сферы – отрезок,
соединяющий любые 2 точки
сферы и проходящий через центр.
т. О – центр сферы
Слайд 58Площадь сферы и шара
Сферу нельзя развернуть на плоскость.
Площадь сферы радиуса R:
Sшара=4 Sкруга
т.е.: площадь поверхности шара равна учетверенной площади большего круга
Слайд 59Задача 2
Найти площадь поверхности сферы,
радиус которой равен 6 см.
Дано:
сфера
Найти:
Sсф = !
Решение:
Sсф = 4πR2
Sсф = 4π 62 = 144π ( см2)
Ответ: 144π см2
Слайд 60
Задача 3
Найти площадь поверхности шара, площадь центрального сечения которого равна 6.
Найти
Найти площадь поверхности шара, площадь центрального сечения которого равна 30,5.
Слайд 61O
№ 4 Вершины треугольника АВС лежат на сфере радиуса 13 см.
102=82+62
Слайд 62O
D
N
B
P
A
O1
C
D
A
B
№ 5 Все стороны ромба, диагонали которого равны 15см и 20см,
M
K
C
K
M
F
Слайд 68Задача
Боковые ребра правильной треугольной пирамиды составляют с основанием угол 60 градусов.
Слайд 69Задача
Длина окружности сечения шара плоскостью, равна 12π см. Расстояние от центра
Слайд 70Задача
Площадь сечения шара плоскостью, проведенной на расстоянии 6 см от центра,
2
Слайд 71Осевое сечение конуса – равносторонний треугольник, периметр которого равен 12√3 см.
Слайд 72.
Осевое сечение цилиндра плоскостью – квадрат, площадь которого равна 36
2