фигуры
Примеры центрально-симметричных фигур
Движение
Теорема
Задача 1
Задача 2
Задача 3
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Центральная симметрия (7 класс)
Содержание
- 1. Презентация по геометрии на тему Центральная симметрия (7 класс)
- 2. содержание Преобразование симметрии относительно точкиСимметричные точкиПостроение 1Построение
- 3. Преобразование симметрии относительно точки О - преобразование
- 4. Точки A и A’,E и E’отрезков АЕ
- 5. Построение 1 Построение симметричных точек.CC’BB’DD’К содержаниюВозьмём точку
- 6. Построение 2 Построение симметричных отрезков.ZNSBCMKOFК содержанию Возьмём
- 7. Построение 3 Построение симметричных треугольников.KК содержаниюA’D’C’MO’ N’M’NO1)
- 8. Построение 4 Построение симметричных четырёхугольников.BACDC’D’A’B’NABCDA’B’C’D’;К содержаниюПостроим четырехугольник,
- 9. Построение 5 Построение симметричных многоугольников.OABCDEFA’B’C’D’E’F’ABCDEFA’B’C’D’E’F’К содержаниюПостроим многоугольник
- 10. SS’OЕсли преобразование симметрииотносительно точки О переводитфигуру в
- 11. примеры центрально-симметричных фигур Параллелограмм : центр симметрии
- 12. Движение Движение – это преобразование одной фигуры
- 13. АОВ= СОЕ (вертикальные) Теорема Преобразование
- 14. Задача 1 При центральной симметрии относительно точки
- 15. Задача 2 При центральной симметрии относительно точки
- 16. Задача 3 При симметрии относительно точки О
содержание Преобразование симметрии относительно точкиСимметричные точкиПостроение 1Построение 2Построение 3Построение 4Построение 5Центрально-симметричные фигуры Примеры центрально-симметричных фигур Движение Теорема Задача 1Задача 2Задача 3
Слайд 2содержание
Преобразование симметрии относительно точки
Симметричные точки
Построение 1
Построение 2
Построение 3
Построение 4
Построение 5
Центрально-симметричные
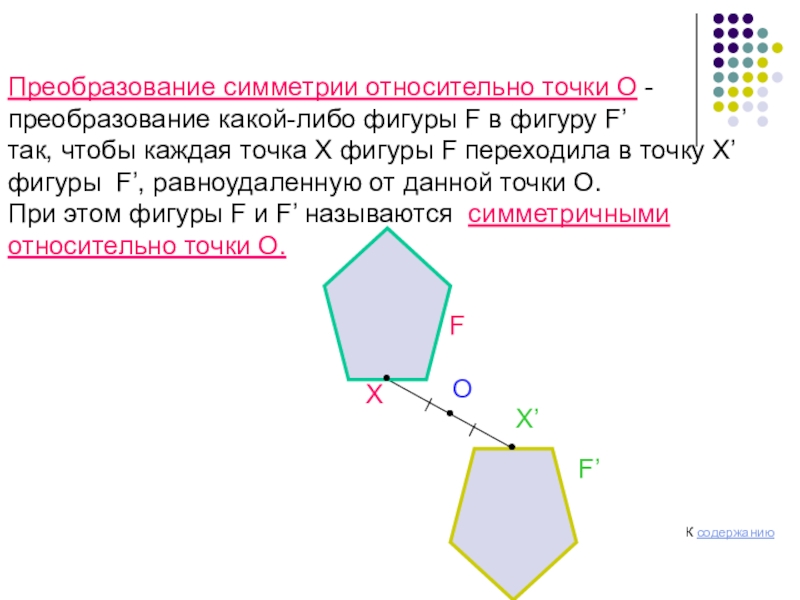
Слайд 3Преобразование симметрии относительно точки О - преобразование какой-либо фигуры F в
фигуру F’
так, чтобы каждая точка Х фигуры F переходила в точку Х’ фигуры F’, равноудаленную от данной точки О.
При этом фигуры F и F’ называются симметричными относительно точки О.
так, чтобы каждая точка Х фигуры F переходила в точку Х’ фигуры F’, равноудаленную от данной точки О.
При этом фигуры F и F’ называются симметричными относительно точки О.
К содержанию
F
F’
X
X’
O
Слайд 4
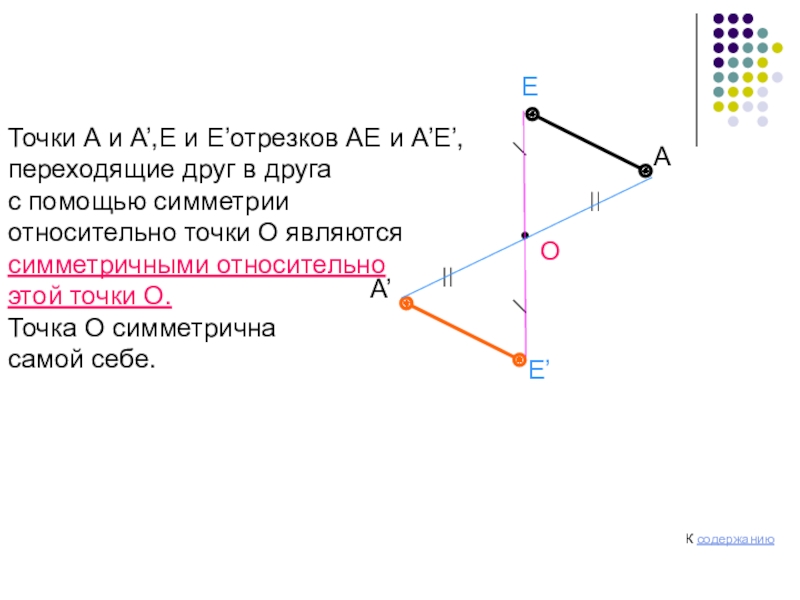
Точки A и A’,E и E’отрезков АЕ и А’Е’,
переходящие друг
в друга
с помощью симметрии
относительно точки О являются
симметричными относительно
этой точки О.
Точка О симметрична
самой себе.
с помощью симметрии
относительно точки О являются
симметричными относительно
этой точки О.
Точка О симметрична
самой себе.
К содержанию
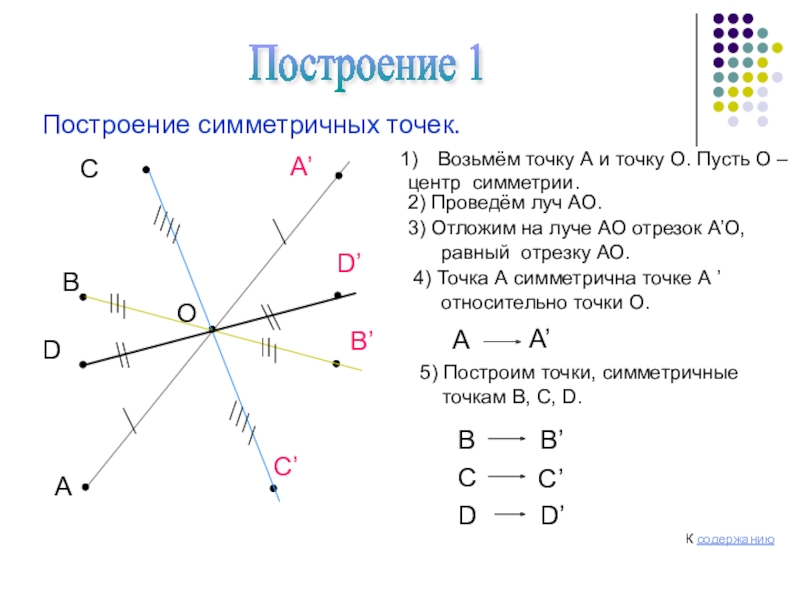
Слайд 5Построение 1
Построение симметричных точек.
C
C’
B
B’
D
D’
К содержанию
Возьмём точку А и точку О.
Пусть О –
центр симметрии.
центр симметрии.
2) Проведём луч АО.
3) Отложим на луче АО отрезок А’О,
равный отрезку АО.
5) Построим точки, симметричные
точкам В, С, D.
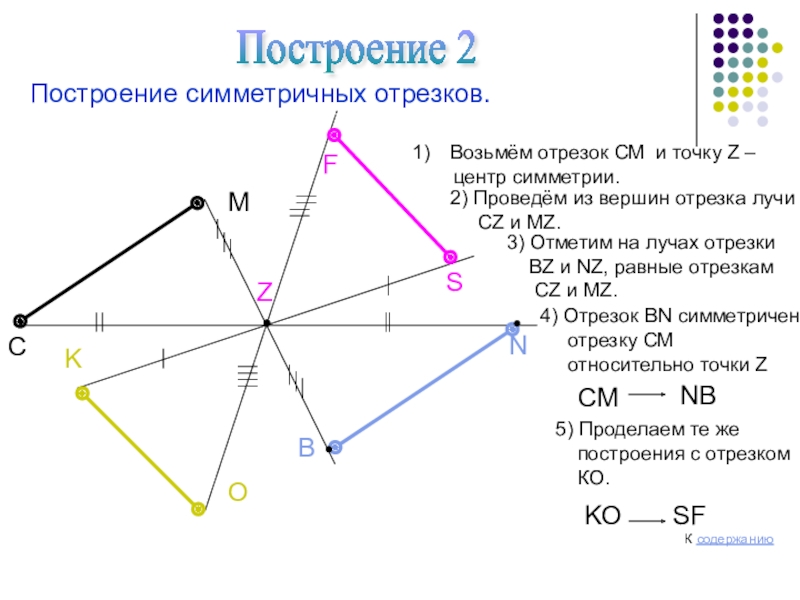
Слайд 6Построение 2
Построение симметричных отрезков.
Z
N
S
B
C
M
K
O
F
К содержанию
Возьмём отрезок СМ и точку
Z –
центр симметрии.
центр симметрии.
2) Проведём из вершин отрезка лучи
СZ и МZ.
3) Отметим на лучах отрезки
ВZ и NZ, равные отрезкам
СZ и МZ.
4) Отрезок ВN симметричен
отрезку СМ
относительно точки Z
5) Проделаем те же
построения с отрезком
КО.
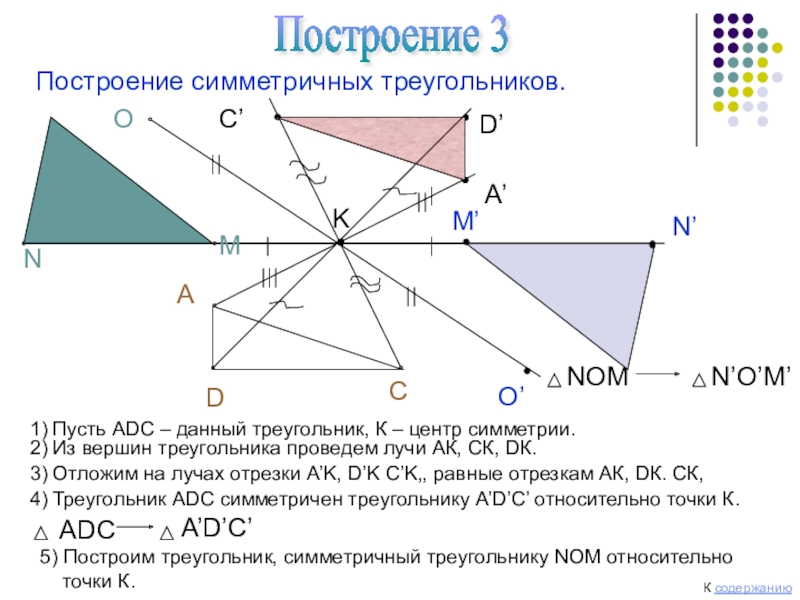
Слайд 7Построение 3
Построение симметричных треугольников.
K
К содержанию
A’
D’
C’
M
O’
N’
M’
N
O
1) Пусть АDС – данный
треугольник, К – центр симметрии.
2) Из вершин треугольника проведем лучи АК, СК, DК.
3) Отложим на лучах отрезки А’K, D’K C’K,, равные отрезкам АК, DК. СК,
4) Треугольник АDС симметричен треугольнику A’D’C’ относительно точки К.
5) Построим треугольник, симметричный треугольнику NОМ относительно
точки К.
Слайд 8
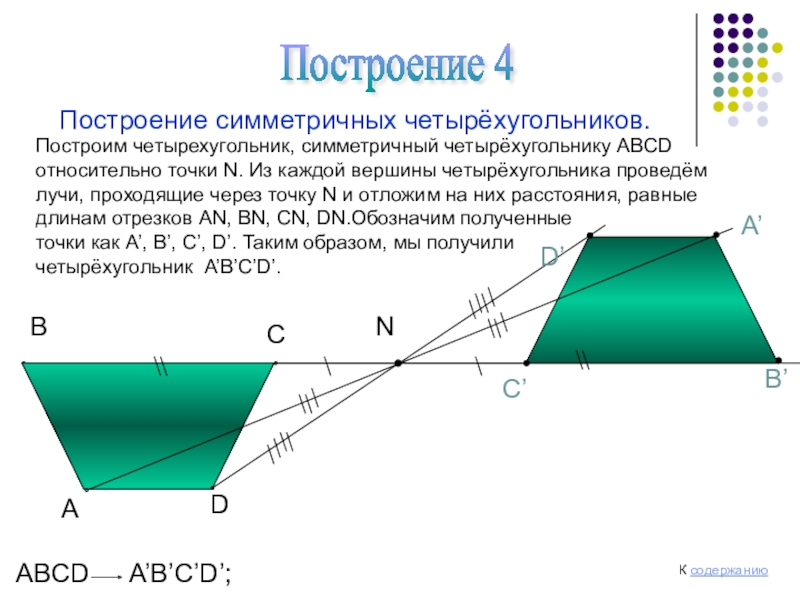
Построение 4
Построение симметричных четырёхугольников.
B
A
C
D
C’
D’
A’
B’
N
ABCD
A’B’C’D’;
К содержанию
Построим четырехугольник, симметричный четырёхугольнику АВСD
относительно
точки N. Из каждой вершины четырёхугольника проведём
лучи, проходящие через точку N и отложим на них расстояния, равные
длинам отрезков AN, BN, CN, DN.Обозначим полученные
точки как A’, B’, C’, D’. Таким образом, мы получили
четырёхугольник A’B’C’D’.
лучи, проходящие через точку N и отложим на них расстояния, равные
длинам отрезков AN, BN, CN, DN.Обозначим полученные
точки как A’, B’, C’, D’. Таким образом, мы получили
четырёхугольник A’B’C’D’.
Слайд 9
Построение 5
Построение симметричных многоугольников.
O
A
B
C
D
E
F
A’
B’
C’
D’
E’
F’
ABCDEF
A’B’C’D’E’F’
К содержанию
Построим многоугольник ,симметричный
многоугольнику АВСDEF относительно
точки О.Проведём из каждой вершины
многоугольника лучи, проходящие через
точку О, и отложим на них расстояния,
равные длинам отрезков АО,ВО, СО, DO,
EO,FO.
Полученные точки обозначим как А’,B’,C’,
D’,E’,F’. Таким образом, мы получили
многоугольник A’B’C’D’E’F’.
Слайд 10
S
S’
O
Если преобразование симметрии
относительно точки О переводит
фигуру в себя, то она называется
центрально-симметричной фигурой,
а точка О называется центром
симметрии.
М
Р
К содержанию
примеры
О
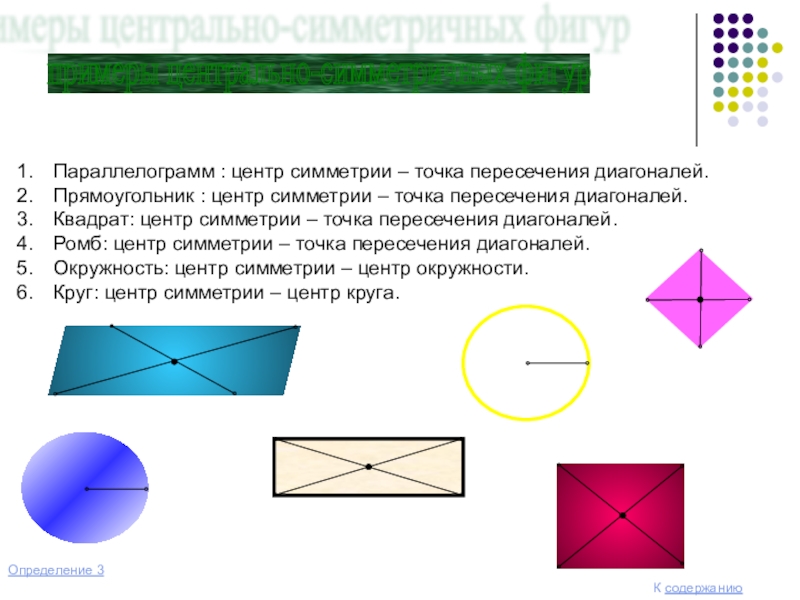
Слайд 11примеры центрально-симметричных фигур
Параллелограмм : центр симметрии – точка пересечения диагоналей.
Прямоугольник
: центр симметрии – точка пересечения диагоналей.
Квадрат: центр симметрии – точка пересечения диагоналей.
Ромб: центр симметрии – точка пересечения диагоналей.
Окружность: центр симметрии – центр окружности.
Круг: центр симметрии – центр круга.
Квадрат: центр симметрии – точка пересечения диагоналей.
Ромб: центр симметрии – точка пересечения диагоналей.
Окружность: центр симметрии – центр окружности.
Круг: центр симметрии – центр круга.
К содержанию
Определение 3
Слайд 12Движение
Движение – это преобразование одной фигуры в
другую так, чтобы сохранялись
расстояния между
точками, то есть так, чтобы любые две точки Х и Y
одной фигуры переходили в точки Х’ и Y’ другой
фигуры, и ХY= Х’ Y’.
точками, то есть так, чтобы любые две точки Х и Y
одной фигуры переходили в точки Х’ и Y’ другой
фигуры, и ХY= Х’ Y’.
Свойства движения
Точки, лежащие на прямой, при движении переходят в точки,
лежащие на прямой, и сохраняется порядок их взаимного расположения.
При движении прямые переходят в прямые, полупрямые – в полупрямые,
отрезки - в отрезки.
При движении сохраняются углы между полупрямыми.
К содержанию
теорема
Слайд 13
АОВ= СОЕ (вертикальные)
Теорема
Преобразование симметрии относительно точки
является
движением.
А
В
С
Е
О
Дано: АВ, О – центр симметрии, АВ
СЕ,
Доказать: АВ СЕ - движение.
Доказательство.
Рассмотрим АОВ и СОЕ.
К содержанию
К движению
Слайд 14Задача 1
При центральной симметрии относительно точки О точка А(-6; 3)
перешла в точку В(10;1), точка С(-3;6) – в точку Е. Найдите
координаты точек О и Е.
координаты точек О и Е.
Решение
К содержанию
Слайд 15Задача 2
При центральной симметрии относительно точки О( 4 ;-2 )
точка
А(-1 ;3) перешла в точку В. Найдите координаты точки В и длину
отрезка АВ.
А(-1 ;3) перешла в точку В. Найдите координаты точки В и длину
отрезка АВ.
Решение.
К содержанию
Слайд 16Задача 3
При симметрии относительно точки О (6;4) точка А с
координатой (0;У)
перешла в точку С (Х;10). Найдите недостающие координаты точек.
перешла в точку С (Х;10). Найдите недостающие координаты точек.
Решение:
К содержанию
