- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Тригонометрические функции(11 класс)
Содержание
- 1. Презентация по геометрии на тему Тригонометрические функции(11 класс)
- 2. Цели:Использование средств алгебры и тригонометрии при решении геометрических задач.Подготовка к ЕГЭ
- 3. Структура урока: мотивационная беседа с последующей постановкой
- 4. Мотивационная беседаЗадачи по стереометрии – прекрасные упражнения,
- 5. Повторим:определения угла между прямыми в пространстве, проекции
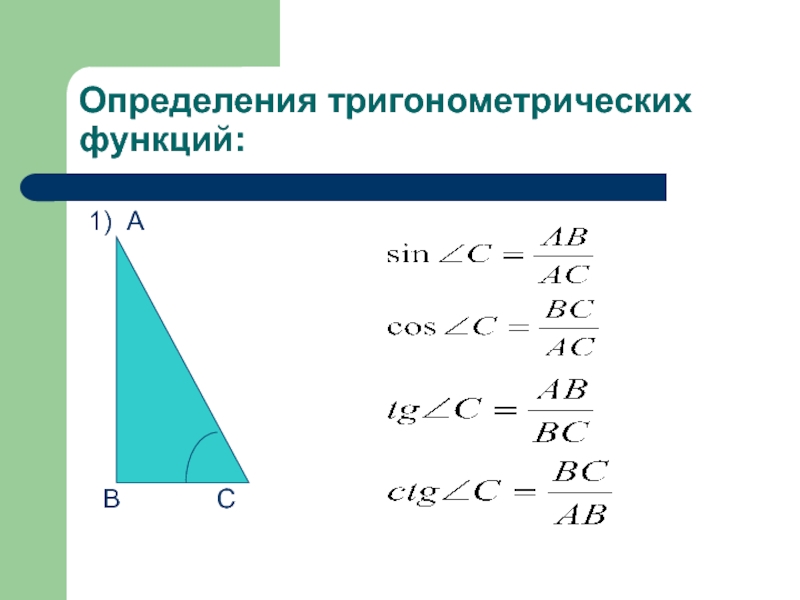
- 6. Определения тригонометрических функций: 1) А
- 7. Определения углов между прямыми, между прямой и
- 8. Определение угла между плоскостями.4)Градусной мерой двугранного угла
- 9. Формулы геометрии с применением тригонометрических функций.1)Площадь треугольника
- 10. Некоторые тригонометрические формулы:1)
- 11. Устный счет (геометрия)1) Ребро куба равно 2
- 12. Устный счет (алгебра)7) Вычислите: соs ²30º –
- 13. рекомендацииРешение геометрической задачи начинается с выполнения чертежа
- 14. Запомни: Тригонометрические функции довольно часто применяются при
- 15. Блок заданий № 1(распечатаны)
- 16. Блок заданий № 2 (дополнительно)(распечатаны)
- 17. Решение уравнения № 11) sin²x- cos²x=0
- 18. Решение задачи № 2S тр= ½•АВ•ВС•sinВ
- 19. Решение задачи №3
- 20. Решение уравнения № 42sin²x-sin x-1=0
- 21. Решение задачи №5
- 22. Задача № 6 Высота правильной треугольной пирамиды равна
- 23. Решение задачи №6 ( способ 1)
- 24. Решение задачи №6 (продолжение)4)Рассмотрим ∆ANH- он прямоугольный. NH/AM=tg
- 25. При решении данной задачи мы использовали метод,
- 26. После того, как задача решена, следует убедиться
- 27. Еще один способ решения задачи №6 Решение
- 28. Работа за компьютеромhttp://fipi.ruОткрытый сегмент ФБТЗМатематикаЗачет 1, 2011 год№ 7,9,13,14
- 29. СОВЕТСЕЙЧАС МОЖНО НАБРАТЬ « Решу ЕГЭ по математике» и решать любой вариант
- 30. Подведение итогов урокаМы замечательно поработали. Те навыки,
- 31. V. Домашнее задание(распечатано) 1. Через сторону основания правильной
- 32. Слайд 32
Слайд 2Цели:
Использование средств алгебры и тригонометрии при решении геометрических задач.
Подготовка к ЕГЭ
Слайд 3Структура урока:
мотивационная беседа с последующей постановкой цели;
актуализация опорных знаний – устная
Диагностика усвоения системы знаний и умений и ее применение для выполнения практических заданий стандартного уровня с переходом на более высокий уровень.
Подведение итогов урока.
Творческое домашнее задание
Рефлексия.
Слайд 4Мотивационная беседа
Задачи по стереометрии – прекрасные упражнения, способствующие развитию пространственных представлений,
Слайд 5Повторим:
определения угла между прямыми в пространстве,
проекции прямой на плоскость,
угла
угла между плоскостями,
а также определения основных тригонометрических функций угла,
некоторые основные тригонометрические формулы и формулы геометрические, в которых используются тригонометрические функции.
Слайд 7Определения углов между прямыми, между прямой и плоскостью.
1)Углом между пересекающимися прямыми
2)Углом между 2-мя скрещивающимися прямыми называется угол между пересекающимися прямыми, параллельными данным.
3)Углом между прямой и плоскостью
пересекающей эту прямую и
не перпендикулярной к ней, называется
угол между прямой и ее проекцией
на данную плоскость.
а
а
а
а
b
b
b
Слайд 8Определение угла между плоскостями.
4)Градусной мерой двугранного угла называется градусная мера его
Слайд 9Формулы геометрии с применением тригонометрических функций.
1)Площадь треугольника = половине произведения двух
угла между ними.
2)Площадь параллелограмма =
произведению двух сторон на синус
угла между ними. S = a•в•SinС
3)Квадрат стороны треугольника =
сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними
с²= а²+b²-2•а•в•CosC
a
в
С
а
в
С
с
а
в
С
Слайд 11Устный счет (геометрия)
1) Ребро куба равно 2 см.Вычислите его объем.
2) Площадь
3) Гипотенуза в прямоугольном треугольнике равна 10 см, а катет 6см. Вычислите другой катет.
4) Могут ли две плоскости иметь общую точку?
5) Ребро куба равно 3см. Вычислите его поверхность.
6) Углы треугольника относятся, как 9:4:5. Вычислите наименьший угол треугольника.
8см²
15см
8см
Нет
54см²
40°
Слайд 12Устный счет (алгебра)
7) Вычислите: соs ²30º – sin² 30º.
8) Вычислите 4sin15º
9) Вычислите argsin√3/2-arccos√2/2+arctg1
10) Известно, что tg ß=1.Вычислите cosß,если
ß- острый угол.
½
1
60°
√2/2
Слайд 13рекомендации
Решение геометрической задачи начинается с выполнения чертежа и анализа; выясняются геометрические
При оформлении нельзя ограничиваться одними вычислениями, необходимо дать полное обоснование решения.
Слайд 14Запомни:
Тригонометрические функции довольно часто применяются при решении стереометрических задач.
Рассмотрим несколько
Слайд 17Решение уравнения № 1
1) sin²x- cos²x=0
1- tg
Sin²x-Cos² x=0 -(Cos²x-Sin²x)=0 Cos 2x=0
2x=± π /2+2 π n x=± π /4+ π n
1-tg x≠0 tg x≠1 x≠ π /4+ π n
Ответ:-π/4+πn, n∈ z.
y
x
π/4
-π/4
0
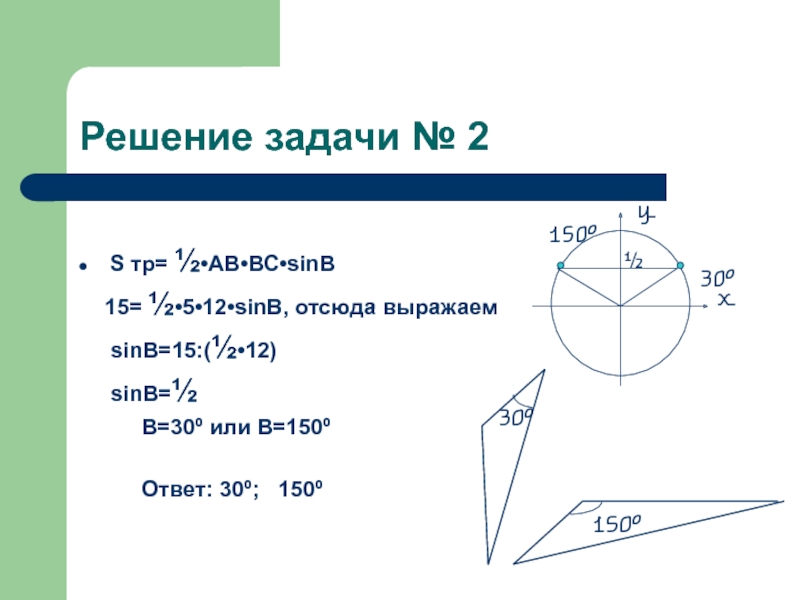
Слайд 18Решение задачи № 2
S тр= ½•АВ•ВС•sinВ
15= ½•5•12•sinВ, отсюда выражаем
sinВ=½
В=30º или В=150º
Ответ: 30º; 150º
x
y
½
30°
150°
30°
150°
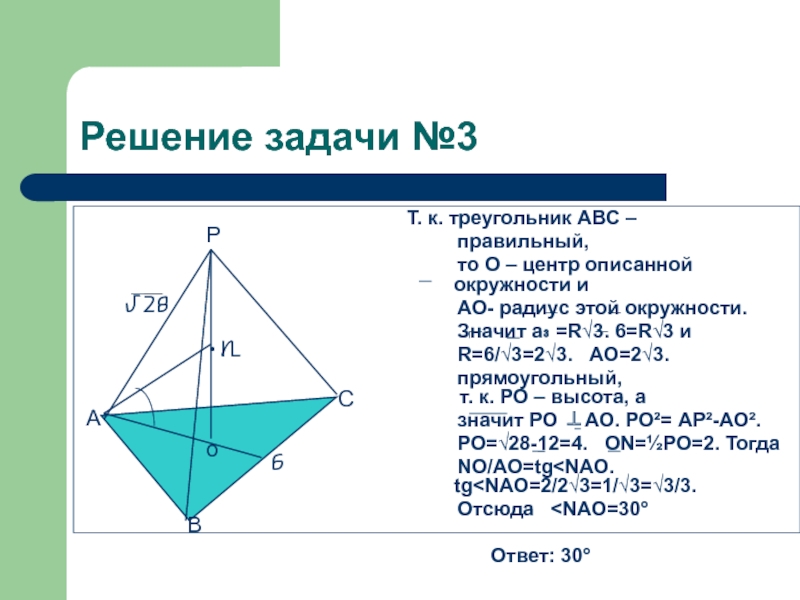
Слайд 19Решение задачи №3
правильный,
то О – центр описанной окружности и
АО- радиус этой окружности.
Значит а₃ =R√3. 6=R√3 и
R=6/√3=2√3. АО=2√3.
прямоугольный, т. к. РО – высота, а
значит РО ⊥АО. РО²= АР²-АО².
РО=√28-12=4. ОN=½РО=2. Тогда
NО/АО=tg
Ответ: 30°
А
В
С
Р
•
N
6
√28
о
Слайд 20Решение уравнения № 4
2sin²x-sin x-1=0 sin
-cos x>0 x= -5 π /6+2 π n
2sin²x-sin x-1=0 -Cos x>0; Cos x<0;
Пусть sin x=m,тогда
2m²-m-1=0
D=1+8=9
m=1;-0,5
Sin x=1; x= π /2+2 π n
Ответ: -5 π /6+2πn, n∈ Z.
0
π /2
- π /6
-5 π /6
- ½
x
y
1
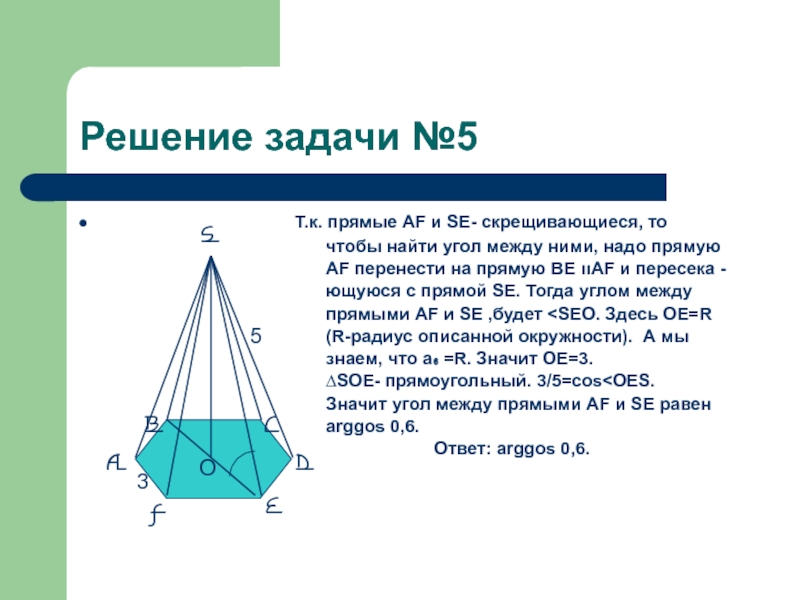
Слайд 21Решение задачи №5
Т.к. прямые АF и SE- скрещивающиеся, то S A F E D C B О 5 3
чтобы найти угол между ними, надо прямую
АF перенести на прямую ВЕ װАF и пересека -
ющуюся с прямой SЕ. Тогда углом между
прямыми AF и SE ,будет
знаем, что а₆ =R. Значит ОЕ=3.
∆SOE- прямоугольный. 3/5=cos
arggos 0,6.
Ответ: arggos 0,6.
Слайд 22Задача № 6
Высота правильной треугольной пирамиды равна стороне её основания, длина
Слайд 23Решение задачи №6 ( способ 1)
Пусть NH – высота
S∆BCL=½ ВС• KL. KL найдем из прямоугольного ∆ ALK.
Поскольку пирамида правильная, то H – центр правильного треугольника ABC. Треугольник BCL – равнобедренный. Чтобы найти его высоту KL, достаточно последовательно вычислить длины отрезков
AK, AH и AN.
1) Из ∆ АКВ : АК= √ АВ²-ВК² = √ a²-(a/2)²=
√a²-a²/4=√3a²/4=(a√3)/2
AK=(a√3)/2
2) Т.к .∆ АВС- равносторонний, то АН-
радиус описанной окружности, т.е.
а3=R√3. Отсюда R=a3/√3
AH=a√3
3)AN=√AH²+HN²=√a²/3+a²=√4a²/3=2a/√3
AN=2a/√3.
N
H
A
B
C
l
K
а
а
Слайд 24Решение задачи №6 (продолжение)
4)Рассмотрим ∆ANH- он прямоугольный. NH/AM=tg
.Значит
S∆=( ВС•KL):2=(а•3a/4):2=3а²/8
ОТВЕТ:.S сечения=3а²/8.
Слайд 25
При решении данной задачи мы использовали метод, который называют поэтапно-вычислительным или
Слайд 26
После того, как задача решена, следует убедиться в правильности решения и
Слайд 27Еще один способ решения задачи №6
Решение этой задачи можно тоже немного
S – площадь данного многоугольника,
S пр – площадь его проекции на плоскость,
f – угол между плоскостью
данными многоугольниками.(
S∆CLB=S∆ABC• Cos
=3а²/8.
.
А
В
С
К
l
N
а
Слайд 28Работа за компьютером
http://fipi.ru
Открытый сегмент ФБТЗ
Математика
Зачет 1, 2011 год
№ 7,9,13,14
Слайд 30Подведение итогов урока
Мы замечательно поработали. Те навыки, которые вы получили на
Слайд 31V. Домашнее задание(распечатано)
1. Через сторону основания правильной треугольной пирамиды проведена плоскость перпендикулярно
2. Рассмотрим правильную четырёхугольную призму ABCDA1B1C1D1, диагональное сечение которой – квадрат. Через вершину D1 и середины рёбер AB и BC проведена плоскость. Найти площадь полученного сечения, если AB = a.