- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Треугольник. Свойства его сторон и углов.
Содержание
- 1. Презентация по геометрии на тему Треугольник. Свойства его сторон и углов.
- 2. Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки,
- 3. Равнобедренный треугольник.Равнобедренный треугольник — это треугольник, в котором две
- 4. Правильный (или равносторонний) треугольник.Правильный (или равносторонний) треугольник — это правильный многоугольник с тремя сторонами, первый из
- 5. Слайд 5
- 6. Медиана. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны треугольника, называется медианой треугольника.
- 7. Свойства точек пересечения медиан. Медианы треугольника пересекаются
- 8. Биссектриса.Биссектрисой треугольника называют отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой на противолежащей стороне.
- 9. Прямоуго́льный треуго́льник.Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то
- 10. Слайд 10
- 11. Внешний угол треугольника.Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
- 12. Как построить внешний угол треугольника? Нужно продлить
- 13. Спасибо за внимание!
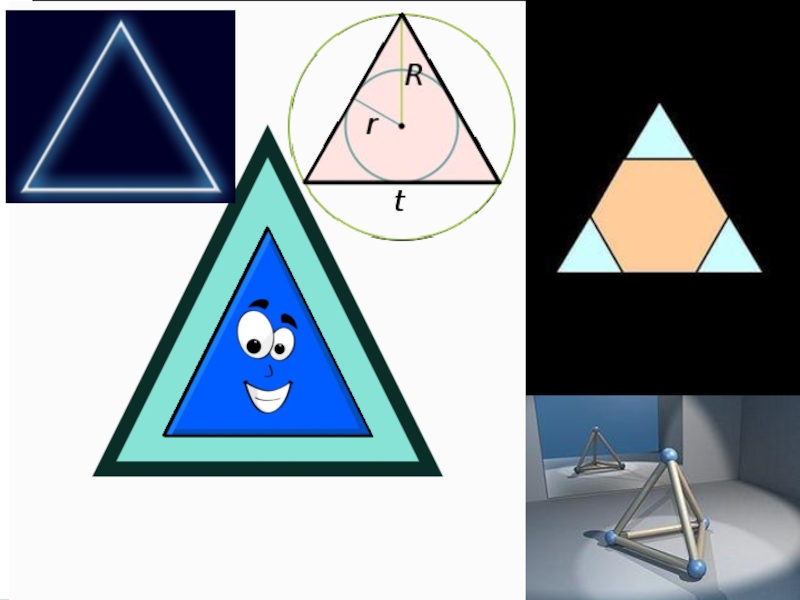
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла.
Слайд 2Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла.
Слайд 3Равнобедренный треугольник.
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой
по длине. Боковыми называются равные стороны, а последняя — основанием. По определению, правильный треугольник также является равнобедренным, но обратное утверждение неверно.
Слайд 4Правильный (или равносторонний) треугольник.
Правильный (или равносторонний) треугольник — это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между
собой, а все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
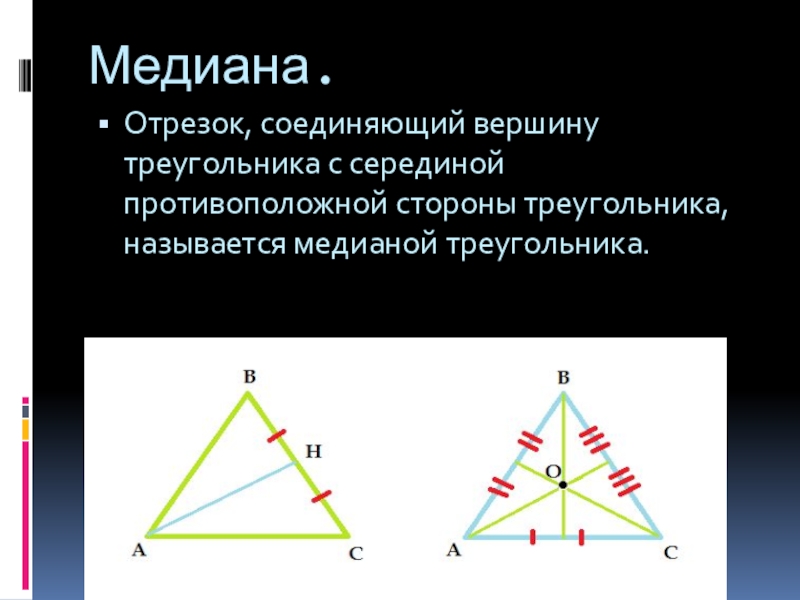
Слайд 6Медиана.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны треугольника, называется
медианой треугольника.
Слайд 7Свойства точек пересечения медиан.
Медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника,
и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Внутренняя медиана угла треугольника изотомически сопряжена самой себе.
Внутренняя медиана угла треугольника изотомически сопряжена самой себе.
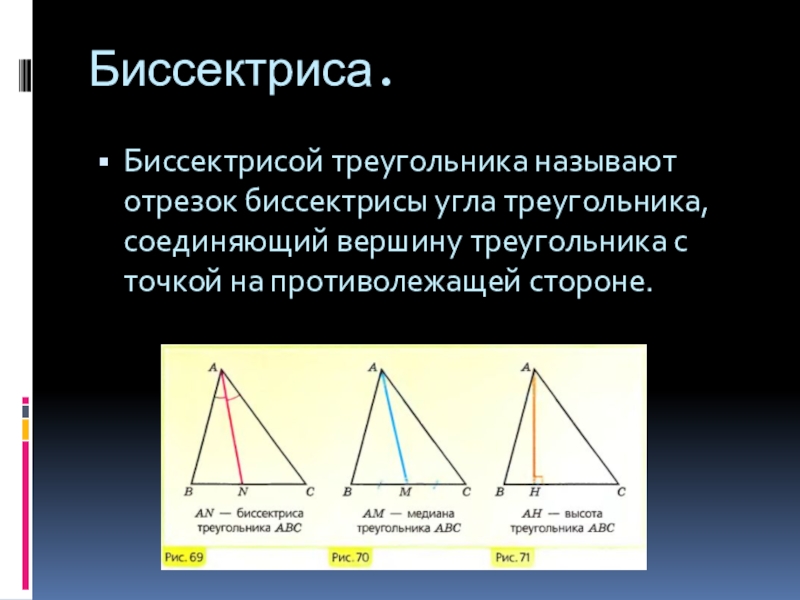
Слайд 8Биссектриса.
Биссектрисой треугольника называют отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с
точкой на противолежащей стороне.
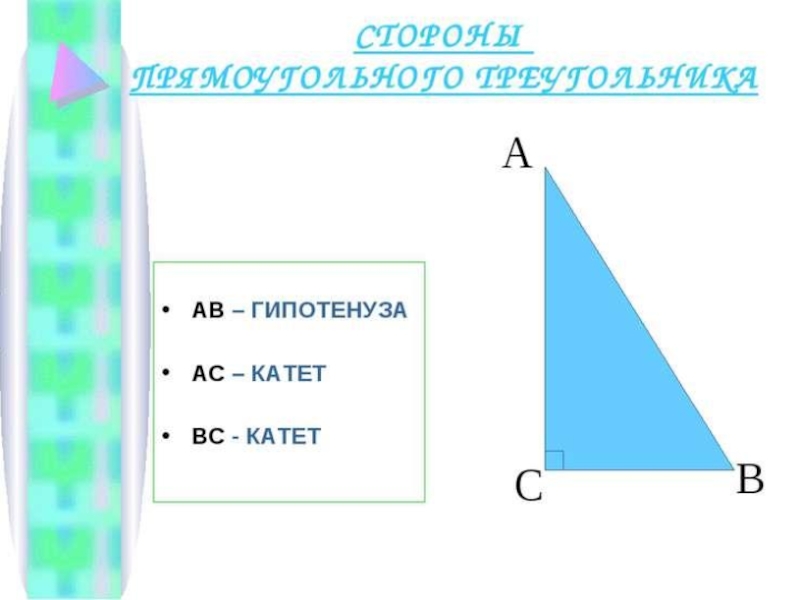
Слайд 9Прямоуго́льный треуго́льник.
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов).
Соотношения между
сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Слайд 11Внешний угол треугольника.
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним
углом треугольника при этой вершине.
Слайд 12Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
На рисунке:
∠3 —
внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
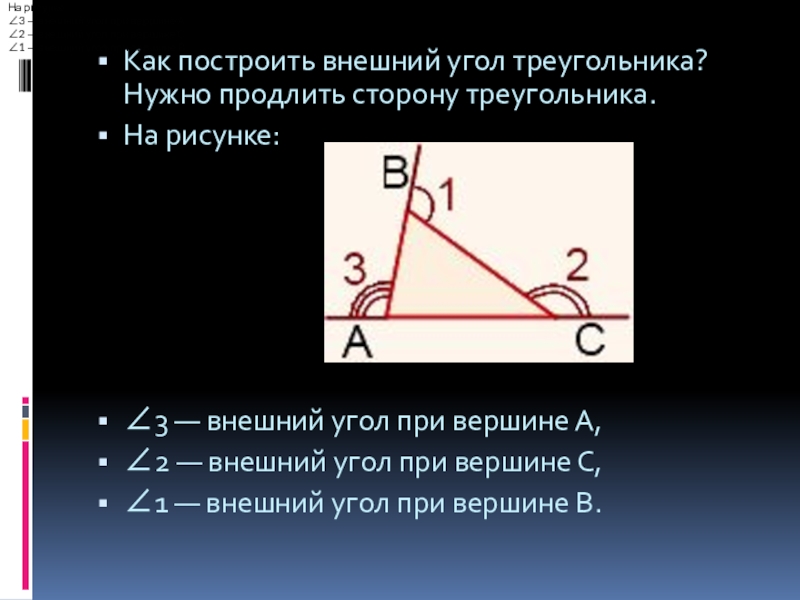
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
На рисунке:
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.