- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора (8 класс)
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора (8 класс)
- 2. Сейчас, пожалуй, не найдется ни одного человека,
- 3. Изображения Пифагорабюст ПифагораПифагор в работе
- 4. Биография Родителями Пифагора были Мнесарх и Партенида с
- 5. По словам античных авторов, Пифагор встретился чуть
- 6. В юном возрасте Пифагор отправился в Египет,
- 7. Позже Пифагор поселился в греческой колонии Кротоне
- 8. Этот орден фактически пришёл в Кротоне к
- 9. А теперь перейдем к самой теореме Пифагора.
- 10. Теорема Пифагора Эту теорему знает каждый школьник. Ее
- 11. Основное доказательство теоремы Рассмотрим прямоугольный треугольник с катетами
- 12. Существует около 100 доказательств теоремы Пифагора. Вот одно из них:
- 13. Доказательство Гарфилда На рисунке 15 три прямоугольных треугольника
- 14. Применение теоремы в жизни Теорема была известна еще
Сейчас, пожалуй, не найдется ни одного человека, которому не знакомо словосочетание «Теорема Пифагора». А кто же такой Пифагор? Давайте познакомимся с его биографией.
Слайд 2 Сейчас, пожалуй, не найдется ни одного человека, которому не знакомо словосочетание
«Теорема Пифагора».
А кто же такой Пифагор? Давайте познакомимся с его биографией.
А кто же такой Пифагор? Давайте познакомимся с его биографией.
Слайд 4Биография
Родителями Пифагора были Мнесарх и Партенида с Самоса. Мнесарх был камнерезом.
Партенида, позднее переименованная мужем в Пифаиду, происходила из знатного рода Анкея, основателя греческой колонии на Самосе. Рождение ребенка будто бы предсказала пифия в Дельфах, потому Пифагор и получил своё имя, которое значит «тот, о ком объявила Пифия».
Партенида сопровождала мужа в его поездках, и Пифагор родился в Сидоне Финикийском (по Ямвлиху) примерно в 570 до н. э.
Партенида сопровождала мужа в его поездках, и Пифагор родился в Сидоне Финикийском (по Ямвлиху) примерно в 570 до н. э.
Слайд 5 По словам античных авторов, Пифагор встретился чуть ли не со всеми
известными мудрецами той эпохи, греками, персами, халдеями, египтянами, впитал в себя всё накопленное человечеством знание.
В популярной литературе иногда приписывают Пифагору Олимпийскую победу в боксе, путая Пифагора-философа с его тёзкой (Пифагором, сыном Кратета с Самоса), который одержал свою победу на 48-х Играх за 18 лет до рождения знаменитого философа.
В популярной литературе иногда приписывают Пифагору Олимпийскую победу в боксе, путая Пифагора-философа с его тёзкой (Пифагором, сыном Кратета с Самоса), который одержал свою победу на 48-х Играх за 18 лет до рождения знаменитого философа.
Слайд 6 В юном возрасте Пифагор отправился в Египет, чтобы набраться мудрости и
тайных знаний у египетских жрецов. Диоген и Порфирий пишут, что самосский тиран Поликрат снабдил Пифагора рекомендательным письмом к фараону Амасису, благодаря чему он был допущен к обучению и посвящён в таинства, запретные для прочих чужеземцев.
Слайд 7 Позже Пифагор поселился в греческой колонии Кротоне в Южной Италии, где
нашёл много последователей. Их привлекала не только оккультная философия, которую он убедительно излагал, но и предписываемый им образ жизни с элементами здорового аскетизма и строгой морали.
Ученики Пифагора образовали своего рода религиозный орден, или братство посвящённых, состоящий из касты отобранных единомышленников, буквально обожествляющих своего учителя и основателя.
Ученики Пифагора образовали своего рода религиозный орден, или братство посвящённых, состоящий из касты отобранных единомышленников, буквально обожествляющих своего учителя и основателя.
Слайд 8 Этот орден фактически пришёл в Кротоне к власти, однако из-за антипифагорейских
настроений в конце VI в. до н. э. Пифагору пришлось удалиться в другую греческую колонию Метапонт, где он и умер.
Почти 450 лет спустя во времена Цицерона (I в. до н. э.) в Метапонте как одну из достопримечательностей показывали склеп Пифагора. У Пифагора была жена по имени Феана, сын Телавг и дочь.
Почти 450 лет спустя во времена Цицерона (I в. до н. э.) в Метапонте как одну из достопримечательностей показывали склеп Пифагора. У Пифагора была жена по имени Феана, сын Телавг и дочь.
Слайд 10Теорема Пифагора
Эту теорему знает каждый школьник.
Ее формулировка звучит так:
в
прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
А записывается она так:
a2+b2=c2,
где a, b – катеты, с - гипотенуза
А записывается она так:
a2+b2=c2,
где a, b – катеты, с - гипотенуза
Слайд 11Основное доказательство теоремы
Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой
c. Докажем, что a2+b2=c2
Достроим треугольник до квадрата со стороной a+b так, как показано на рисунке. Площадь этого квадрата равна (a + b)2. С другой стороны, этот квадрат состоит из четырех равных прямоугольных треугольников, площадь каждого из которых равна 0,5ab и квадрата со стороной с, поэтому
откуда
Достроим треугольник до квадрата со стороной a+b так, как показано на рисунке. Площадь этого квадрата равна (a + b)2. С другой стороны, этот квадрат состоит из четырех равных прямоугольных треугольников, площадь каждого из которых равна 0,5ab и квадрата со стороной с, поэтому
откуда
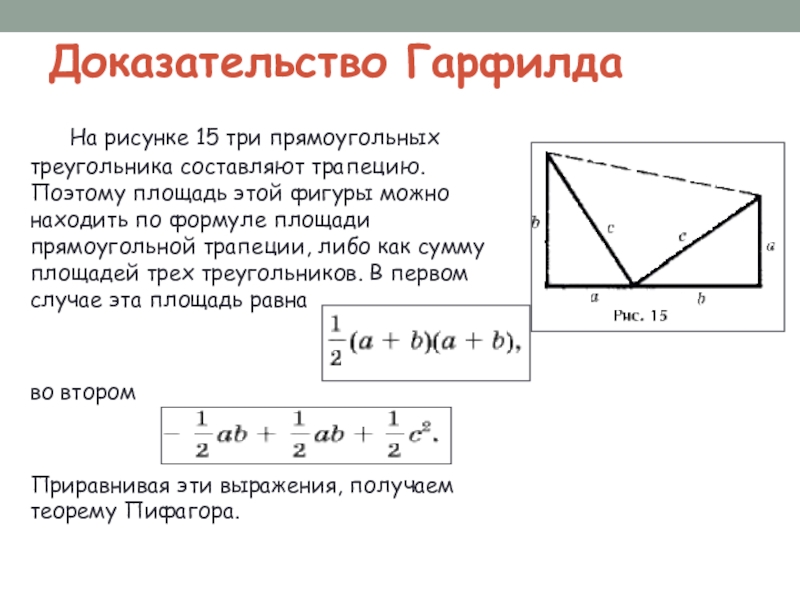
Слайд 13Доказательство Гарфилда
На рисунке 15 три прямоугольных треугольника составляют трапецию. Поэтому площадь
этой фигуры можно находить по формуле площади прямоугольной трапеции, либо как сумму площадей трех треугольников. В первом случае эта площадь равна
во втором
Приравнивая эти выражения, получаем теорему Пифагора.
во втором
Приравнивая эти выражения, получаем теорему Пифагора.
Слайд 14Применение теоремы в жизни
Теорема была известна еще до появления Пифагора, но
только он смог точно сформулировать ее и доказать.
Еще в Древнем Египте пользовались этой теоремой для постройки зданий. Они знали что треугольник со сторонами 3, 4, 5 – прямоугольный. В строительстве эта теорема применяется по сей день.
Еще в Древнем Египте пользовались этой теоремой для постройки зданий. Они знали что треугольник со сторонами 3, 4, 5 – прямоугольный. В строительстве эта теорема применяется по сей день.