- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора (8 класс)
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора (8 класс)
- 2. «Числа управляют миром. Все вещи- суть числа.
- 3. Неизвестно, каким способом доказывал Пифагор свою теорему.
- 4. Сохранилась легенда, которая гласит, что, доказав свою
- 5. Один из способов доказательства теоремы Пифагора.1) После
- 6. АMDCcc1234babaB
- 7. Доказательство может быть проведено на фигуре, в
- 8. Произведем преобразование для квадрата, построенного на катете а :а)
Слайд 1Различные способы доказательства теоремы Пифагора.
Подготовила ученица 8в класса
МБОУ гимназии
Киселёва Екатерина .
Слайд 2«Числа управляют миром. Все вещи- суть числа. Все прекрасно благодаря числу».
Пифагор
Теорема Пифагора окружена богатейшим историческим материалом, связанным с её появлением и способами доказательства. Изучение истории развития геометрии прививает любовь к данному предмету, способствует развитию познавательного интереса, общей культуры и творчества.
Слайд 3Неизвестно, каким способом доказывал Пифагор свою теорему. Несомненно лишь то, что
Слайд 4Сохранилась легенда, которая гласит, что, доказав свою знаменитую теорему, Пифагор принес
Слайд 5Один из способов доказательства теоремы Пифагора.
1) После изучения темы «Подобные треугольники»
Рассмотрим прямоугольный треугольник с прямым углом С, СD– высота. Докажем, что АС² +СВ² = АВ².
Доказательство:
На основании утверждения о катете прямоугольного треугольника:
АС = , СВ =
Возведем в квадрат и сложим полученные равенства:
АС² = АВ * АD, СВ² = АВ * DВ;
АС² + СВ² = АВ * ( АD + DВ), где АD+DB=AB, тогда
АС² + СВ² = АВ * АВ,
АС² + СВ² = АВ².
Слайд 6А
M
D
C
c
c
1
2
3
4
b
a
b
a
B
Пусть катет b, а. Продолжим отрезок СВ за точку В и построим треугольник BMD так, чтобы точки М и А лежали по одну сторону от прямой CD и, кроме того, BD = b, BDM = 90°, DM = a, тогда
BMD =
по двум сторонам и углу между ними.
Точки А и М соединим отрезками AM. Имеем MD CD и AC CD, значит, прямая АС параллельна прямой MD. Так как MD < АС, то прямые CD и AM не параллельны. Следовательно, AMDC - прямоугольная трапеция.
ABC
В прямоугольных треугольниках ABC и BMD
1 +
2= 90 и
3 +
4= 90, но так как
1=
3, то
3+
2= 90
тогда
АВМ =180° - 90° = 90°. Оказалось, что трапеция AMDC разбита на три неперекрывающихся
прямоугольных треугольника, тогда по аксиомам площадей.
или
Разделив все члены неравенства на ½ , получим
аb + с2 + аb = (а + b)2, 2ab + с2 = а2 + 2аb + b2,
с2 = а2 + b2.
Доказательство закончено.
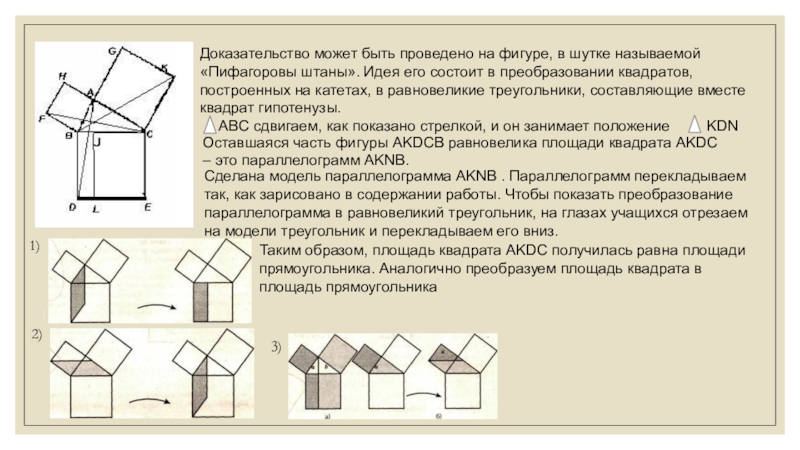
Слайд 7Доказательство может быть проведено на фигуре, в шутке называемой «Пифагоровы штаны».
ABC сдвигаем, как показано стрелкой, и он занимает положение
KDN
1)
2)
3)
Оставшаяся часть фигуры AKDCB равновелика площади квадрата AKDC – это параллелограмм AKNB.
Сделана модель параллелограмма AKNB . Параллелограмм перекладываем так, как зарисовано в содержании работы. Чтобы показать преобразование параллелограмма в равновеликий треугольник, на глазах учащихся отрезаем на модели треугольник и перекладываем его вниз.
Таким образом, площадь квадрата AKDC получилась равна площади прямоугольника. Аналогично преобразуем площадь квадрата в площадь прямоугольника
Слайд 8Произведем преобразование для квадрата, построенного на катете а :
а) квадрат преобразуется в равновеликий
б) параллелограмм поворачивается на четверть оборота
в) параллелограмм преобразуется в равновеликий прямоугольник.