- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Менелая
Содержание
- 1. Презентация по геометрии на тему Теорема Менелая
- 2. Менелай Александрийский Менела́й Александри́йский- древнегреческий математик
- 3. Книга «Сферика»Главное сочинение Меналая — «Сферика» в
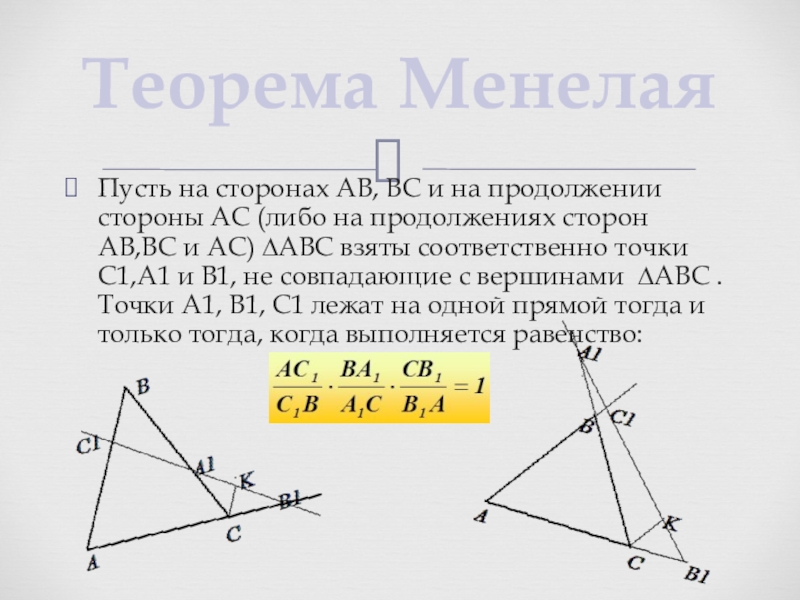
- 4. Пусть на сторонах AB, BC и на
- 5. Пусть точки А1, В1 и С1 лежат
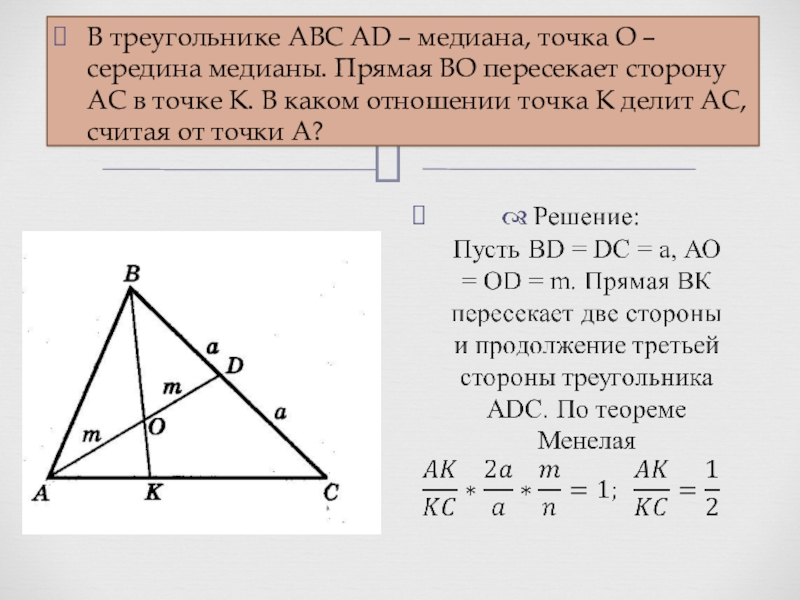
- 6. Решение задачВ треугольнике АВС АD – медиана,
- 7. Слайд 7
- 8. Теорема Менелая не изучается в основном курсе
- 9. Литература:Геометрия.10-11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / А.В.Погорелов.-12-е изд.-М.:Просвещение,2012Интернет
Слайд 2 Менелай Александрийский
Менела́й Александри́йский- древнегреческий математик и астроном. Автор работ
Слайд 3Книга «Сферика»
Главное сочинение Меналая — «Сферика» в трёх книгах. Его греческий
В I книге «Сферики» дается определение сферического треугольника и связанных с ним понятий. В 39 предложении этой книги речь идёт о свойствах сферических треугольников.
В 21 предложении II книги рассматриваются свойства системы параллельных кругов на сфере при пересечении их разными большими кругами — как проходящими через общие полюсы этого семейства, так и наклонными по отношению к этим полюсам. Эта книга опирается на «Сферику» Феодосия.
Книге III предшествуют леммы о составных отношениях, на которых строятся дальнейшие доказательства. Эта книга открывается теоремой о полном четырёхстороннике (известной также как «теорема шести величин» или «теорема о трансверсалях»). Она доказывается сначала для плоского случая, а затем переносится центральным проектированием на сферу. При этом Менелай формулирует её сферический вариант не на языке отношений синусов, как это стали делать впоследствии Ибн Ирак и другие математики стран ислама, но на языке отношений хорд.
Слайд 4Пусть на сторонах AB, BC и на продолжении стороны AC (либо
Теорема Менелая
Слайд 5Пусть точки А1, В1 и С1 лежат на одной прямой. Докажем,
Проведем прямые AD,BM и CN параллельно прямой В1А1. Согласно обобщению теоремы Фалеса имеем:
и
Перемножая левые и правые части этих равенств, получаем:
, откуда
Доказательство
C
B
A
D
N
M
Слайд 6Решение задач
В треугольнике АВС АD – медиана, точка О – середина
Слайд 8Теорема Менелая не изучается в основном курсе геометрии 7–9 классов. Решение
Вывод
Слайд 9Литература:
Геометрия.10-11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни /
Интернет