О
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема о вписанном угле(8 класс)
Содержание
- 1. Презентация по геометрии на тему Теорема о вписанном угле(8 класс)
- 2. Вписанные углыЦветочная клумбаДана клумба круглой формы, на
- 3. Вписанные углыПлан УРОКА Изучить определение вписанного углаНаучиться
- 4. Вписанные углыУглы :Угол – геометрическая фигура, которая
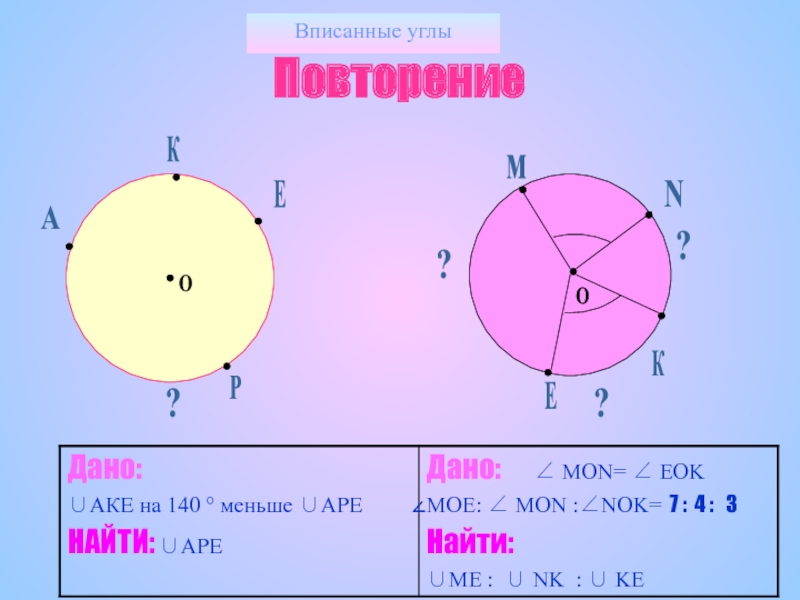
- 5. Вписанные углыПовторениемКЕNКЕAP????ОО
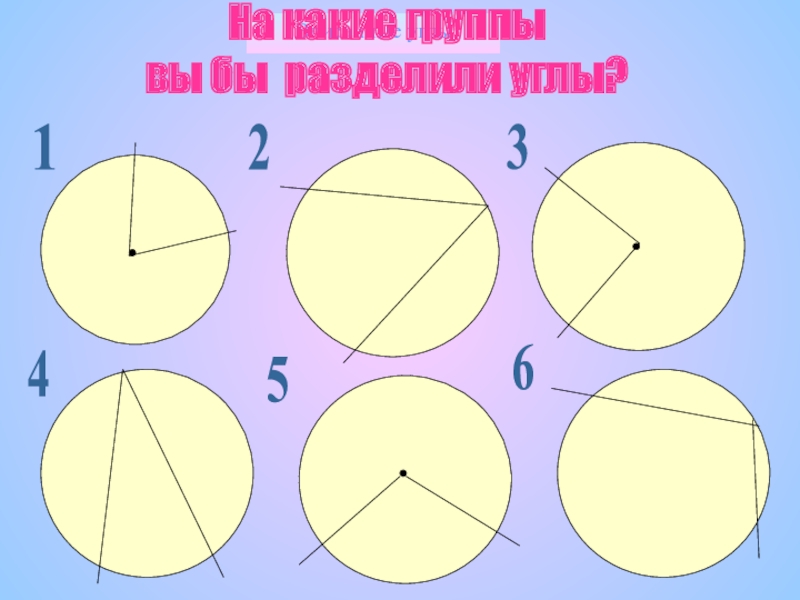
- 6. Вписанные углыНа какие группы вы бы разделили
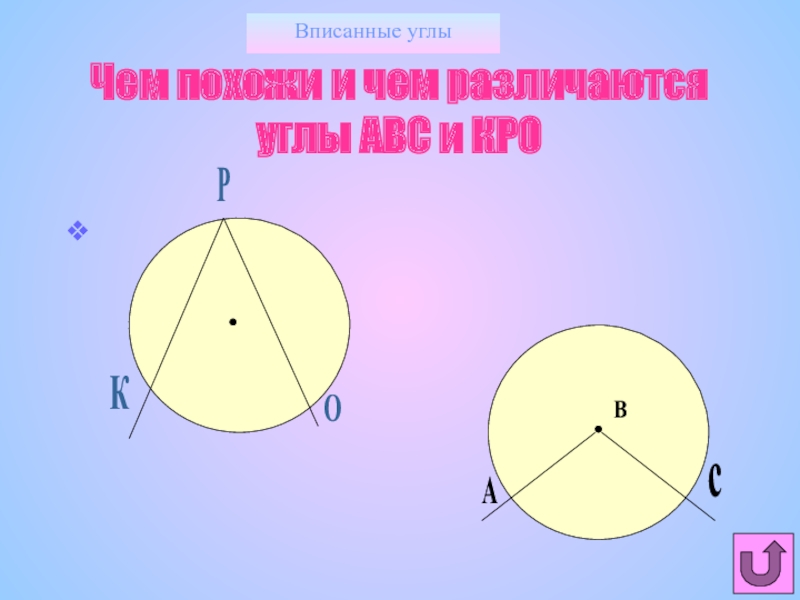
- 7. Вписанные углыЧем похожи и чем различаются углы АВС и КРО ВАсКРО
- 8. Вписанные углыОпределениеУгол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным.АВСО
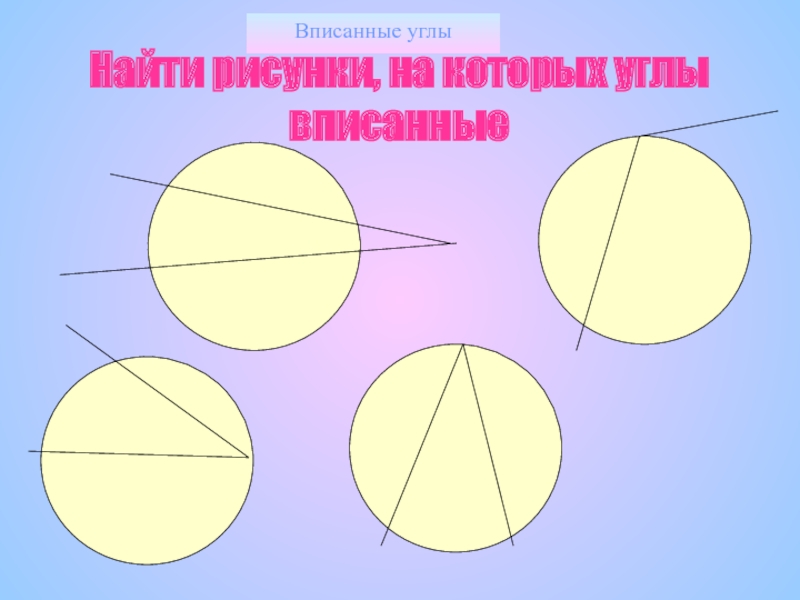
- 9. Вписанные углыНайти рисунки, на которых углы вписанные
- 10. Вписанные углыАОВС
- 11. Вписанные углыТеорема о вписанном угле Вписанный угол
- 12. Вписанные углы Теорема
- 13. Вписанные углы2 случай Луч ВО делит угол
- 14. Вписанные углы3 случай Луч ВО НЕ
- 15. Вписанные углы
- 16. Вписанные углыО
- 17. Вписанные углыСледствияВписанные углы, опирающиеся на одну и
- 18. Вписанные углыСледствие №1АВС = АКС,
- 19. Вписанные углыСледствие №2АВС = 90,так как он опирается на развёрнутый угол, градусная мера которого равна 180.
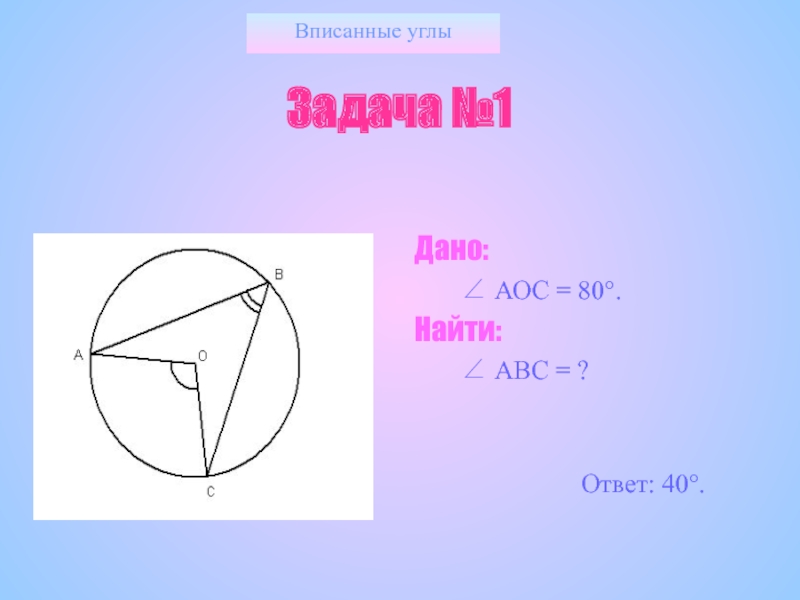
- 20. Вписанные углыЗадача №1Дано: АОС = 80.Найти: АВС
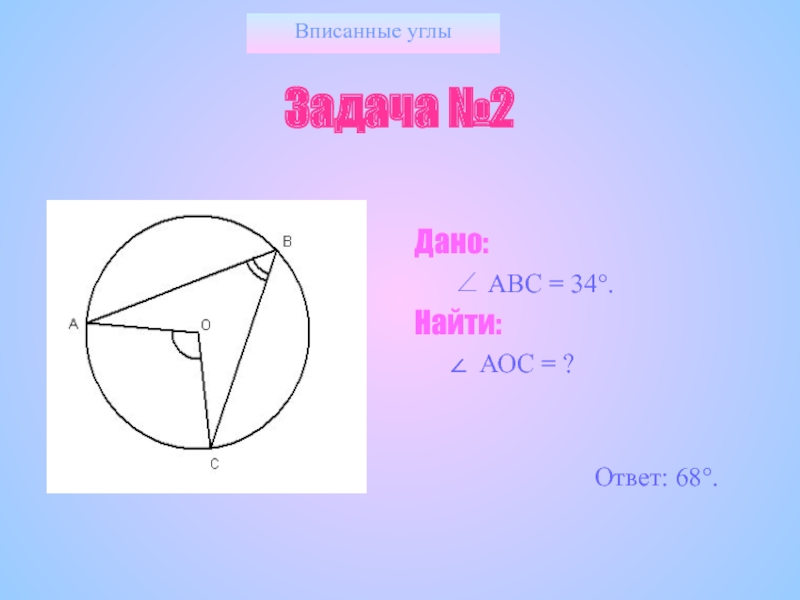
- 21. Вписанные углыЗадача №2Дано: АВС = 34°.Найти:АОС =
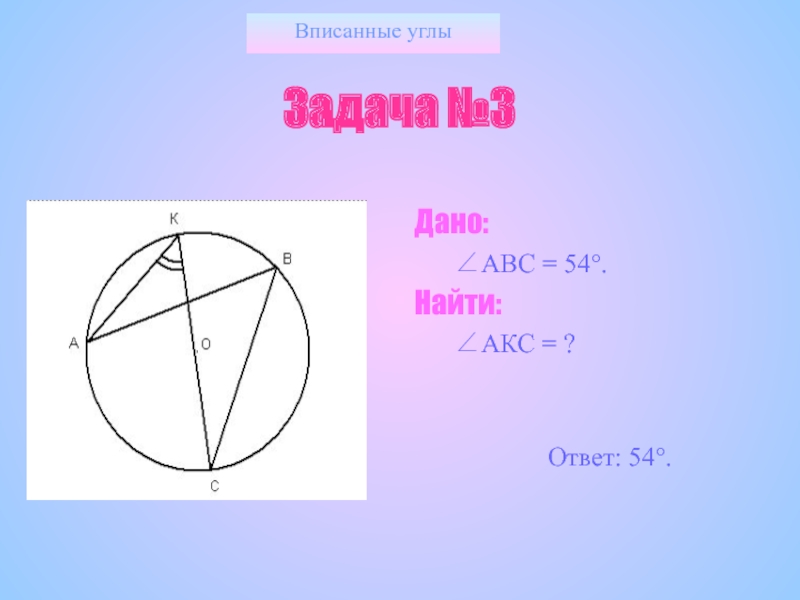
- 22. Вписанные углыЗадача №3Дано:АВС = 54.Найти:АКС = ? Ответ: 54.
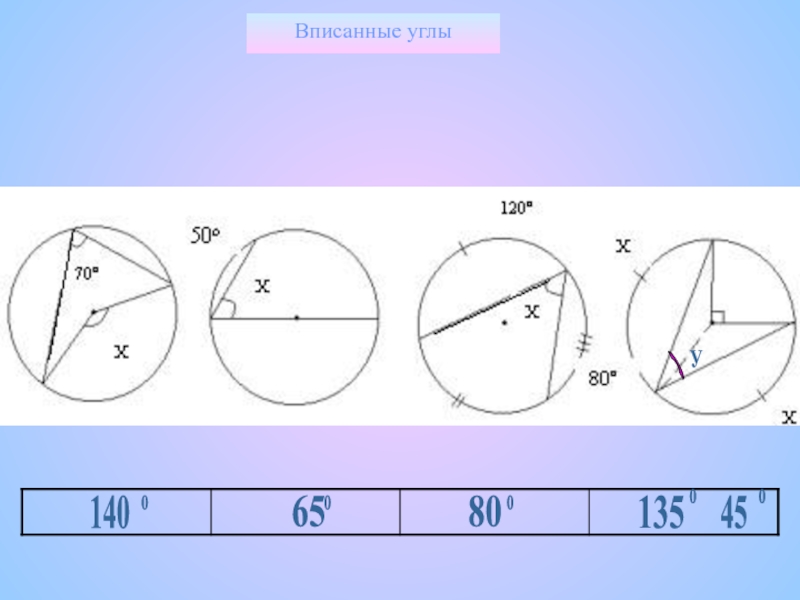
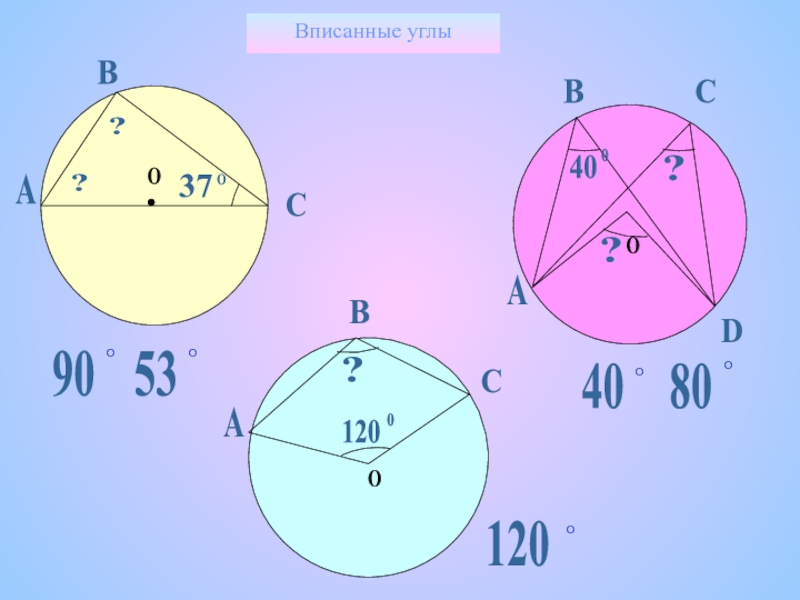
- 23. Вписанные углы У140658013545ооооо
- 24. Вписанные углыО37О??АВСООААВВССD40oo???1209053°°4080°°°120
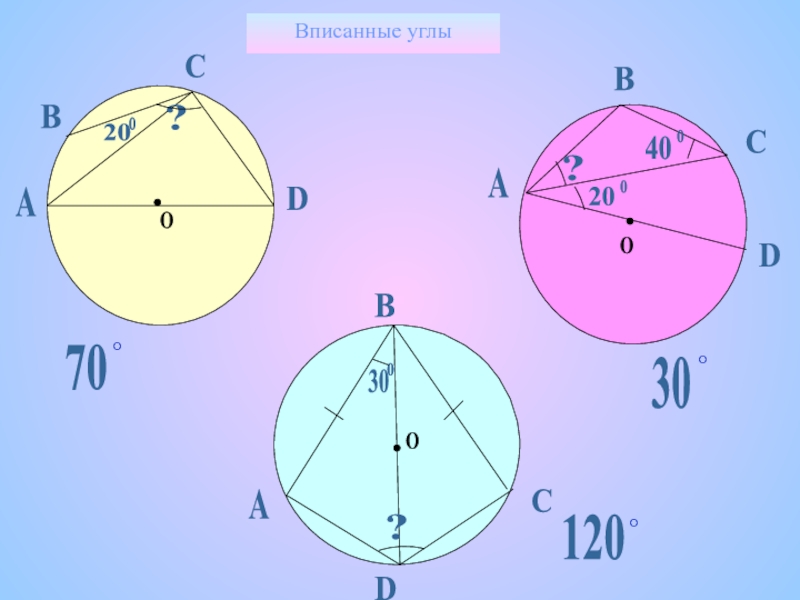
- 25. Вписанные углы20oОВСD?АО20oo40o?АВСDО30?АВСD70°°°30120
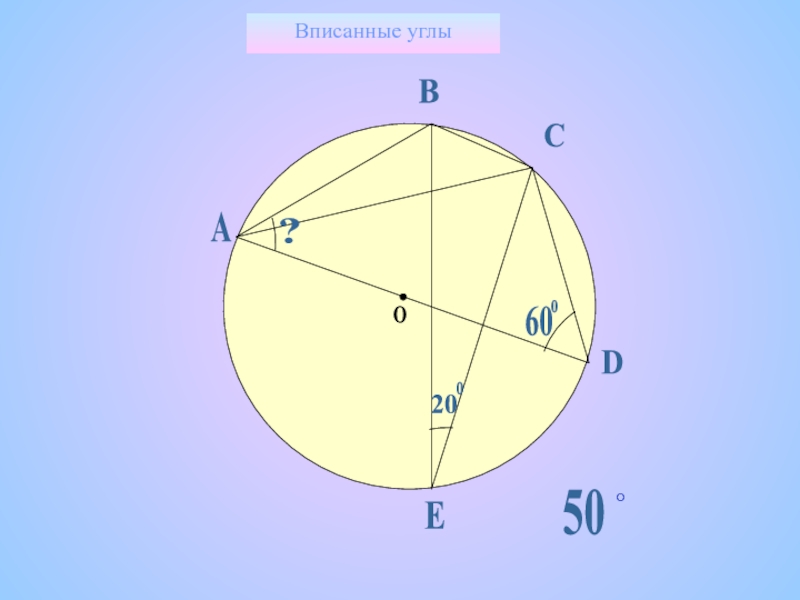
- 26. Вписанные углы20o60oО?АВСDЕ50°
- 27. Вписанные углыИгра на повторение «Веришь — не веришь» Верите ли вы,
- 28. Вписанные углыРабота по тесту с программированным контролем решения.
- 29. Вписанные углыОтветы
- 30. Вписанные углыРабота по тесту с программированным контролем решения.
- 31. Вписанные углыПроверка домашнего задания. Задача на вычисление суммы углов пятиконечной звезды, вписанной в окружность
- 32. Вписанные углыI способ: Угол
- 33. Вписанные углыI I способ: Когда вершины пятиугольной
- 34. Вписанные углыСофизм –доказательство ложного утверждения, причем ошибка
- 35. Хорда, не проходящая через центр, равна диаметру.Пусть
- 36. Найдем ошибкуПо теореме о признаке равенства треугольника:Если
- 37. Вписанные углыТест на оптическую иллюзию по рисункам
- 38. Вписанные углыТест 1 1.
- 39. Вписанные углы Тест 2
- 40. Вписанные углыЦветочная клумбаДана клумба круглой формы, на
- 41. Вписанные углыУсвоив теорему овеличине вписанного угла в
- 42. Вписанные углыДомашнее задание. п. 71, выучить определение
- 43. Вписанные углыБлагодарю за внимание!
Слайд 2Вписанные углы
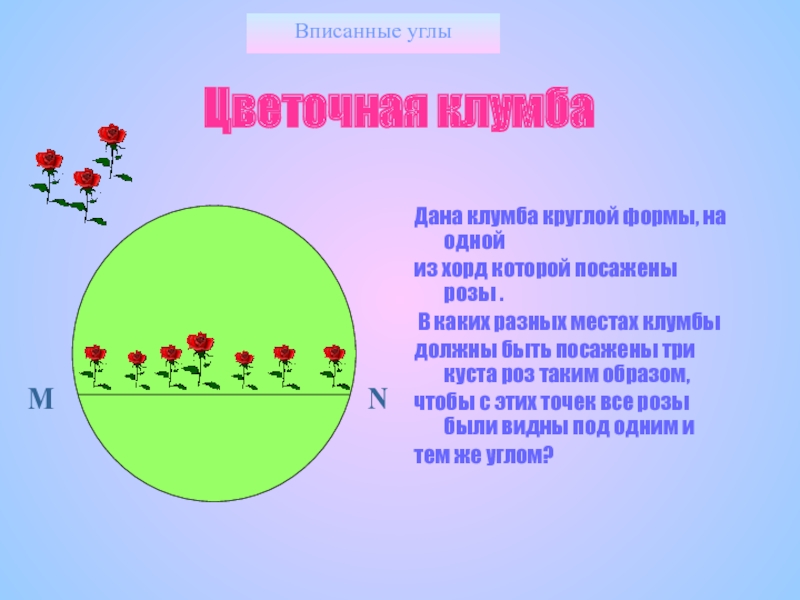
Цветочная клумба
Дана клумба круглой формы, на одной
из хорд которой посажены
В каких разных местах клумбы
должны быть посажены три куста роз таким образом,
чтобы с этих точек все розы были видны под одним и
тем же углом?
М
N
Слайд 3Вписанные углы
План УРОКА
Изучить определение вписанного угла
Научиться распознавать вписанные углы на
Узнать, какими свойствами обладают вписанные углы
Научиться применять полученные знания при решение задач
Слайд 4Вписанные углы
Углы :
Угол –
геометрическая фигура, которая состоит из точки
Центральный угол –
угол с вершиной в центре окружности.
О
А
В
Слайд 8Вписанные углы
Определение
Угол, вершина которого лежит на окружности, а стороны пересекают окружность,
вписанным.
А
В
С
О
Слайд 11Вписанные углы
Теорема о вписанном угле
Вписанный угол измеряется половиной дуги,
Слайд 12Вписанные углы
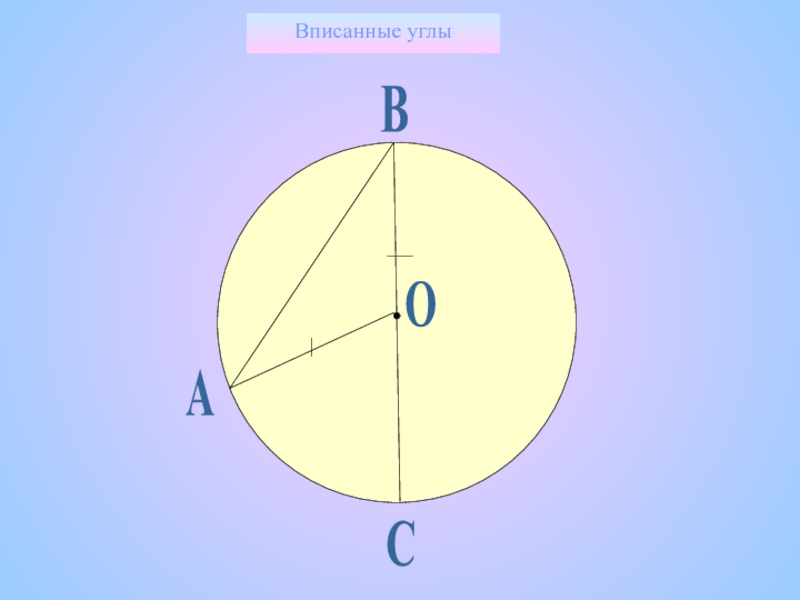
Теорема о вписанном угле
1 случай
Дано: Окр (О; R)
АВС – вписанный угол
Доказать:
АВС = ½ АС
Доказательство:
1.АОВ – равнобедренный,
так как ОВ = ОА = R, значит, В = А.
2. СОА – внешний угол, следовательно,
СОА = ОВА + ОАВ
СОА = 2 ОВА, значит,
ОВА = ½ СОА
СВА = ½ АС.
А
В
С
О
Слайд 13Вписанные углы
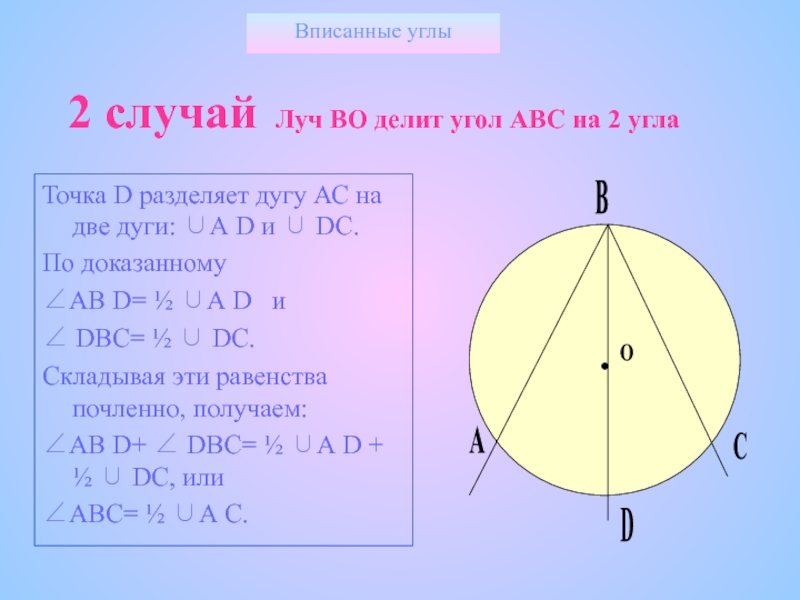
2 случай Луч ВО делит угол АВС на 2 угла
Точка
По доказанному
АВ D= ½ А D и
DВС= ½ DС.
Складывая эти равенства почленно, получаем:
АВ D+ DВС= ½ А D + ½ DС, или
АВС= ½ А С.
А
В
С
D
О
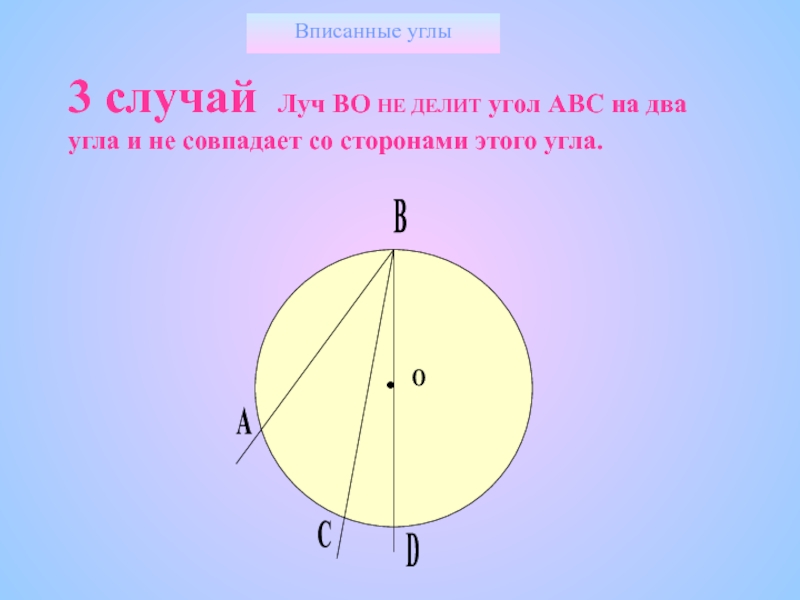
Слайд 14Вписанные углы
3 случай Луч ВО НЕ ДЕЛИТ угол АВС на
А
В
D
С
О
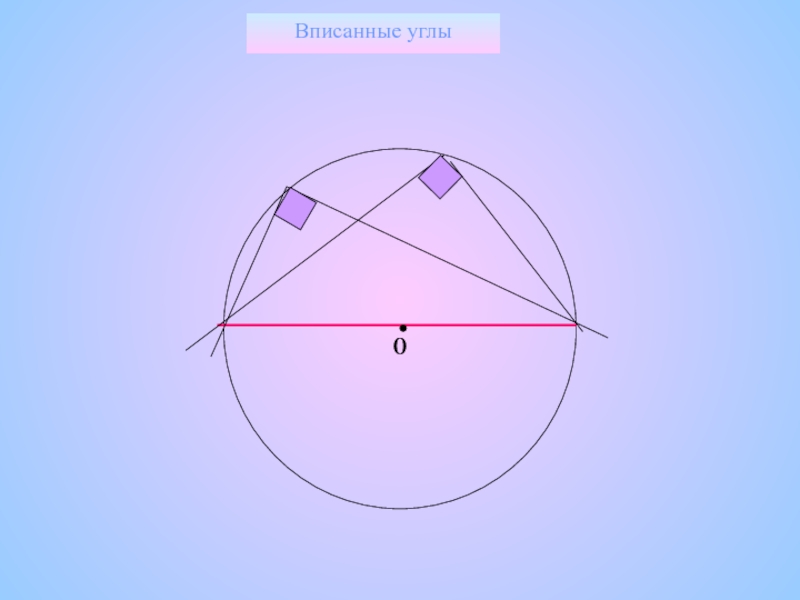
Слайд 17Вписанные углы
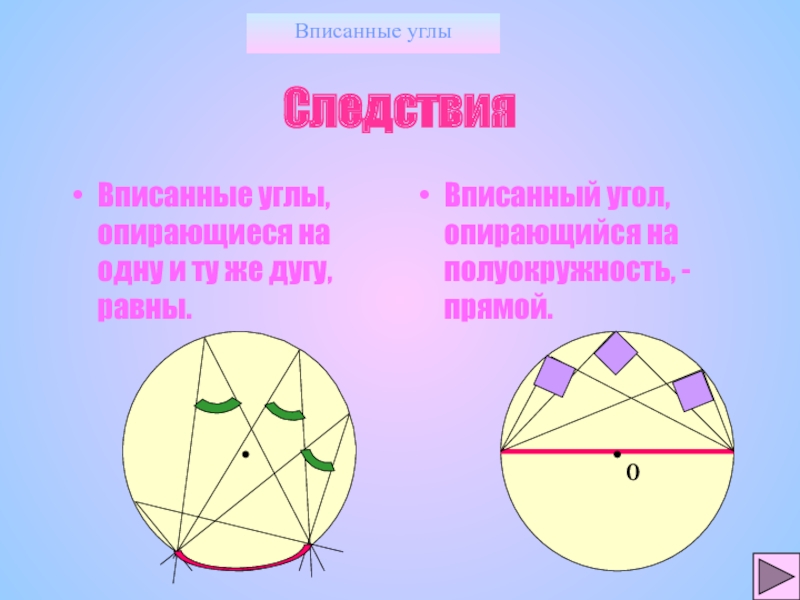
Следствия
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность, - прямой.
О
Слайд 18Вписанные углы
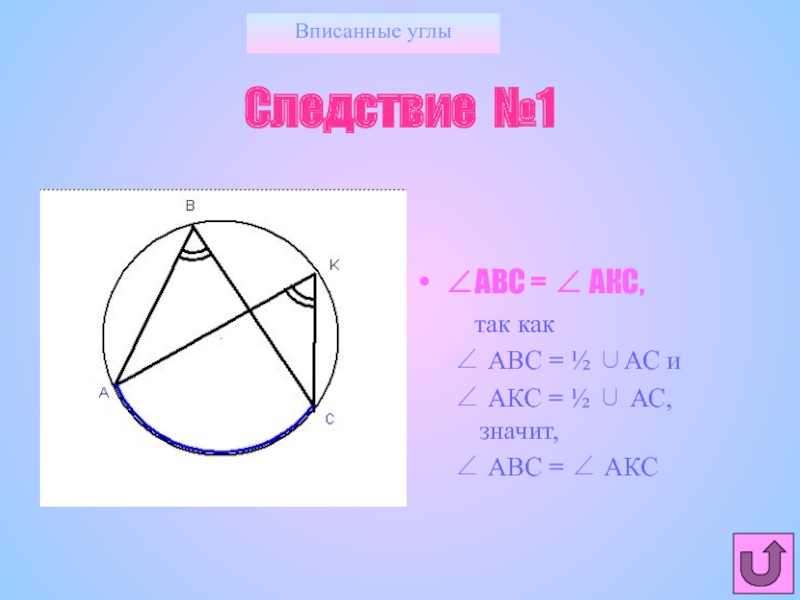
Следствие №1
АВС = АКС,
так как
АВС
АКС = ½ АС, значит,
АВС = АКС
Слайд 19Вписанные углы
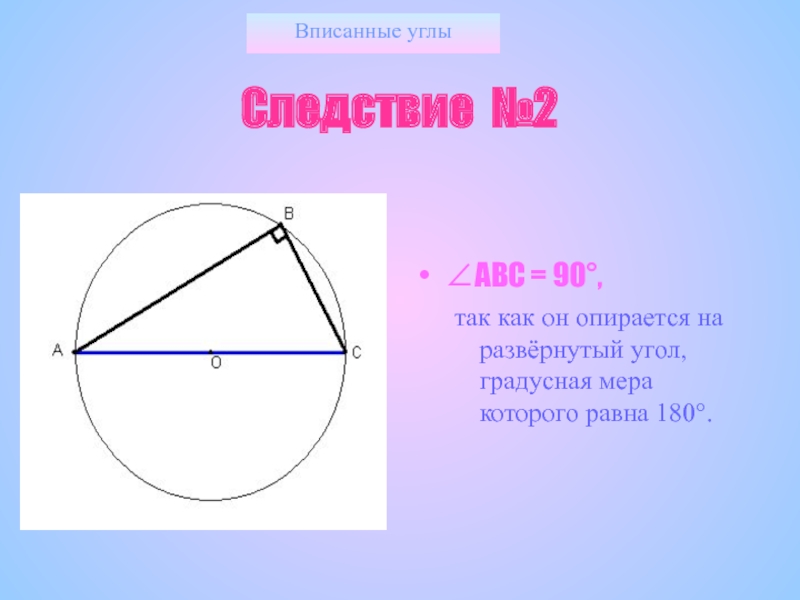
Следствие №2
АВС = 90,
так как он опирается на развёрнутый угол,
Слайд 27Вписанные углы
Игра на повторение «Веришь — не веришь»
Верите ли вы, что если величина центрального
Верите ли вы, что отрезки касательных к окружности равны и составляют равные углы с прямой, проходящей через центр окружности?
Верите ли вы, что угол проходящий через центр окружности называется ее центральным углом?
Верите ли вы, что вписанный угол измеряется половиной дуги, на которую он опирается?
Верите ли вы, что величина центрального угла в два раза больше величины дуги, на которую он опирается?
Верите ли вы, что вписанный угол, опирающийся на полуокружность равен 180˚ ?
Верите ли вы, что угол, стороны которого пересекают окружность называется вписанным углом?
Верите ли вы, что вписанные углы, опирающиеся на одну и ту же дугу равны?
Верите ли вы, что при дальнейшем изучении материала с окружностью будут связаны не только углы, но и треугольники и четырехугольники?
Нет, отрезки касательных к окружности (проведенные из одной точки) равны и составляют равные углы с прямой, проходящей через (эту точку и) центр окружности.
ДА, если величина центрального угла равна 90˚, то вписанный угол, опирающийся на эту дугу равен 45˚.
Нет, угол проходящий (выходящий из) через центр окружности называется ее центральным углом.
Да, вписанный угол измеряется половиной дуги, на которую он опирается.
Нет, величина центрального угла в два раза больше (равна) величины дуги, на которую он опирается.
Нет, вписанный угол, опирающийся на полуокружность равен 180˚ (прямой) .
Нет, угол, стороны которого пересекают окружность (а вершина лежит на окружности) называется вписанным углом.
Да, вписанные углы, опирающиеся на одну и ту же дугу равны.
Да, при дальнейшем изучении материала с окружностью будут связаны не только углы, но и треугольники и четырехугольники.
Слайд 31Вписанные углы
Проверка домашнего задания.
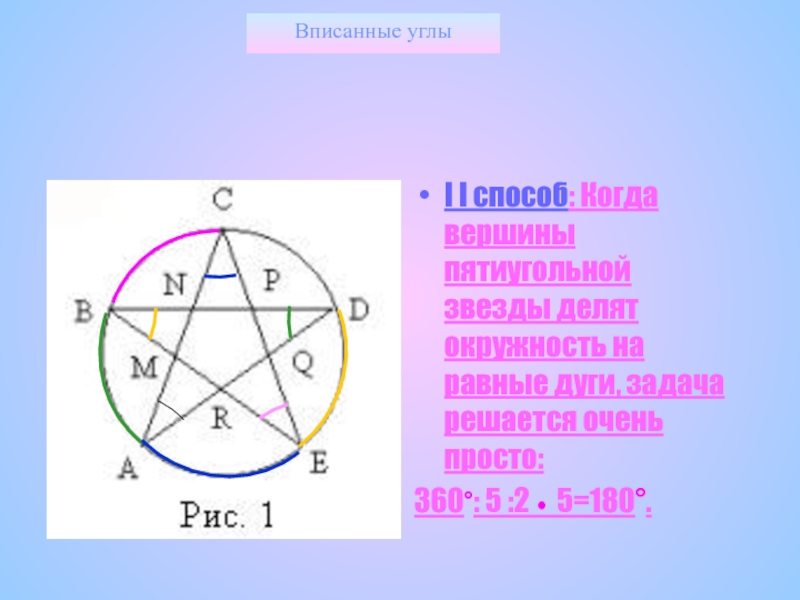
Задача на вычисление суммы углов пятиконечной звезды,
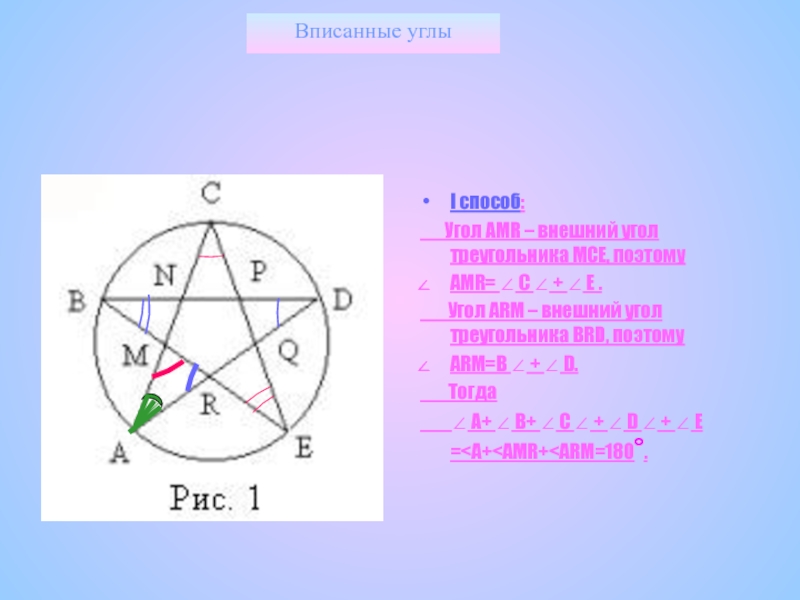
Слайд 32Вписанные углы
I способ:
Угол AMR – внешний
AMR= C + E .
Угол ARM – внешний угол треугольника BRD, поэтому
ARM=B + D.
Тогда
A+ B+ C + D + E =
Слайд 33Вписанные углы
I I способ: Когда вершины пятиугольной звезды делят окружность на
360°: 5 :2 5=180°.
Слайд 34Вписанные углы
Софизм –доказательство ложного утверждения, причем ошибка в доказательстве искусно замаскирована.
Слайд 35Хорда, не проходящая через центр, равна диаметру.
Пусть в окружности проведен диаметр
же сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны.
Значит, ▲ ВDА= ▲ ЕDC, а в равных треугольниках против равных углов лежат равные стороны.
Поэтому, АВ=ЕС.
А
В
Е
С
D
О
Слайд 36Найдем ошибку
По теореме о признаке равенства треугольника:
Если сторона и два прилежащих
А в нашем случае,
угол А не прилежит к стороне ВD.
А
В
Е
С
D
О
Слайд 37Вписанные углы
Тест на оптическую иллюзию по рисункам с альтернативным ответом.
Оптическую иллюзию
Слайд 38Вписанные углы
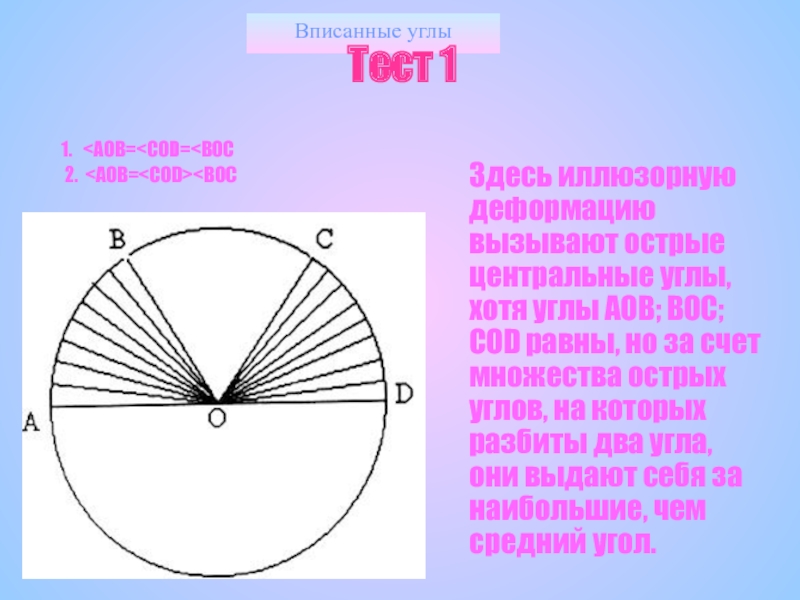
Тест 1
1.
Слайд 39Вписанные углы
Тест 2
В окружность вписан:
1. квадрат
2. близкая к квадрату фигура
Тест 2, 3: Здесь доминирующими являются окружности. Углы вписанные в окружность, образуют в первом случае квадрат, во втором правильный треугольник. Эти фигуры за счет множества окружностей выдают себя, как фигуры приближенные к квадрату и треугольнику. Стороны кажутся вогнутыми во внутрь.
Итак, иллюзию мы можем применять на практике, в повседневной жизни. Например, с ее помощью можно скрывать недостатки формы лица, фигуры.
В окружность вписан:
1. треугольник
2. близкая к треугольнику фигура
Слайд 40Вписанные углы
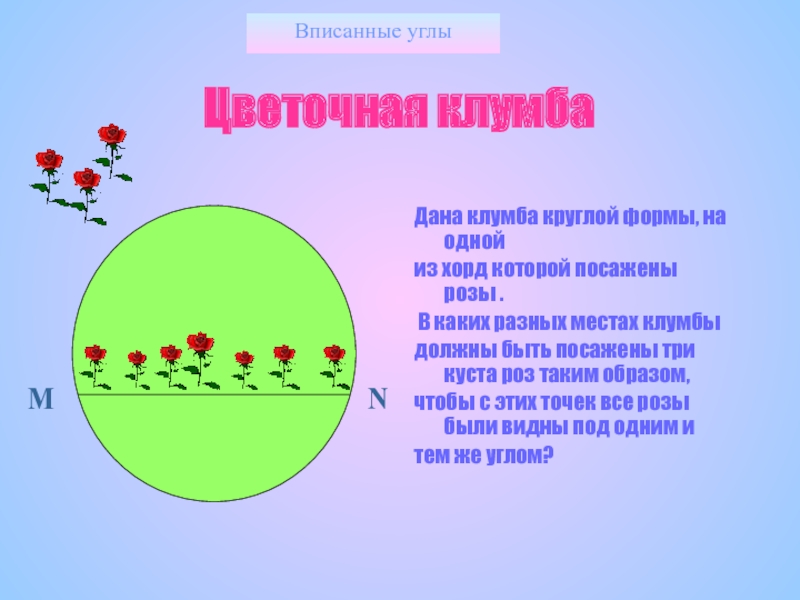
Цветочная клумба
Дана клумба круглой формы, на одной
из хорд которой посажены
В каких разных местах клумбы
должны быть посажены три куста роз таким образом,
чтобы с этих точек все розы были видны под одним и
тем же углом?
М
N
Слайд 41Вписанные углы
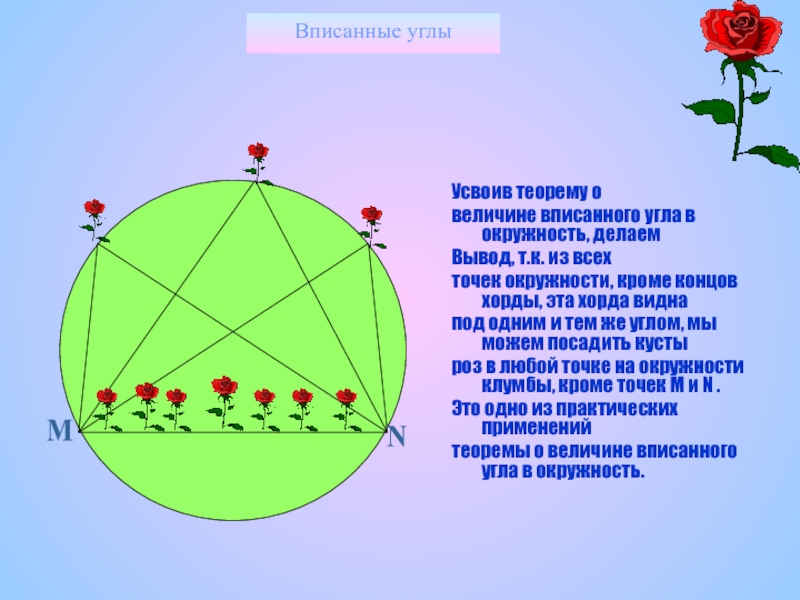
Усвоив теорему о
величине вписанного угла в окружность, делаем
Вывод, т.к. из
точек окружности, кроме концов хорды, эта хорда видна
под одним и тем же углом, мы можем посадить кусты
роз в любой точке на окружности клумбы, кроме точек М и N .
Это одно из практических применений
теоремы о величине вписанного угла в окружность.
М
N
Слайд 42Вписанные углы
Домашнее задание.
п. 71, выучить определение вписанного угла;
выучить теорему о
№ 654 № 656 № 657