по пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременною. На каком расстоянии от более высокой пальмы появилась раба.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Телрема Пифагора
Содержание
- 1. Презентация по геометрии на тему: Телрема Пифагора
- 2. Старинная задачаНа
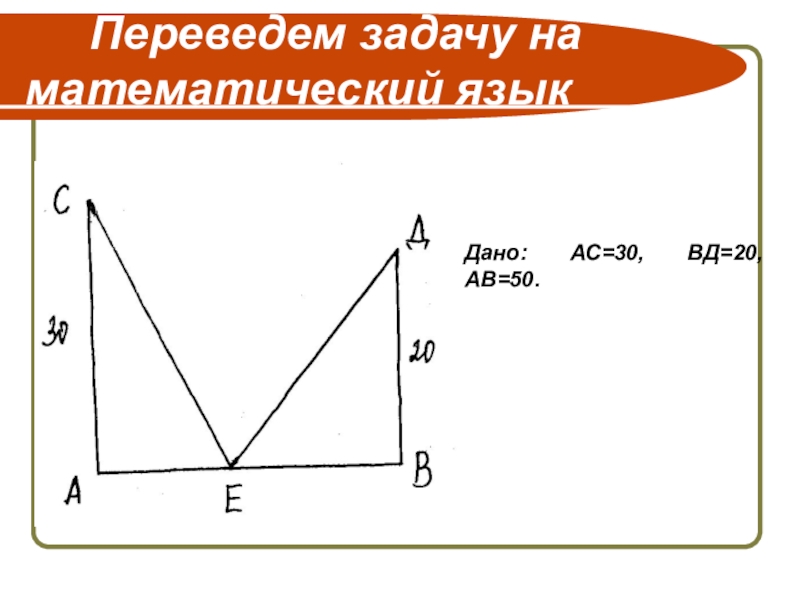
- 3. Переведем задачу на математический языкДано: АС=30, ВД=20, АВ=50.
- 4. Нужно знать зависимость между катетами и гипотенузой
- 5. Биография Пифагора Пифагор-это не имя,
- 6. Пифагорейская школа Вернувшись на родину,
- 7. Пифагорейская школа Пифагорейцы
- 8. Заповеди Пифагора и
- 9. Заповеди пифагорийцевДелать то, что
- 10. Физминутка
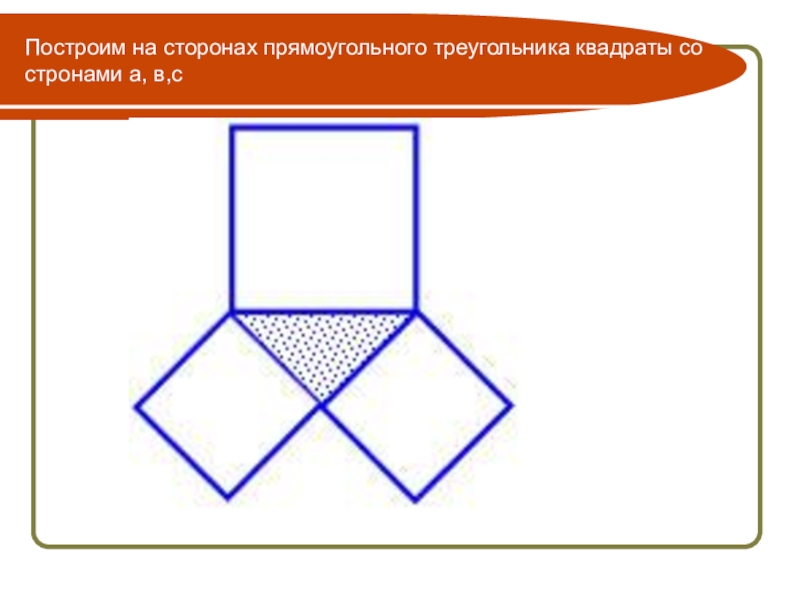
- 11. Построим на сторонах прямоугольного треугольника квадраты со стронами а, в,с
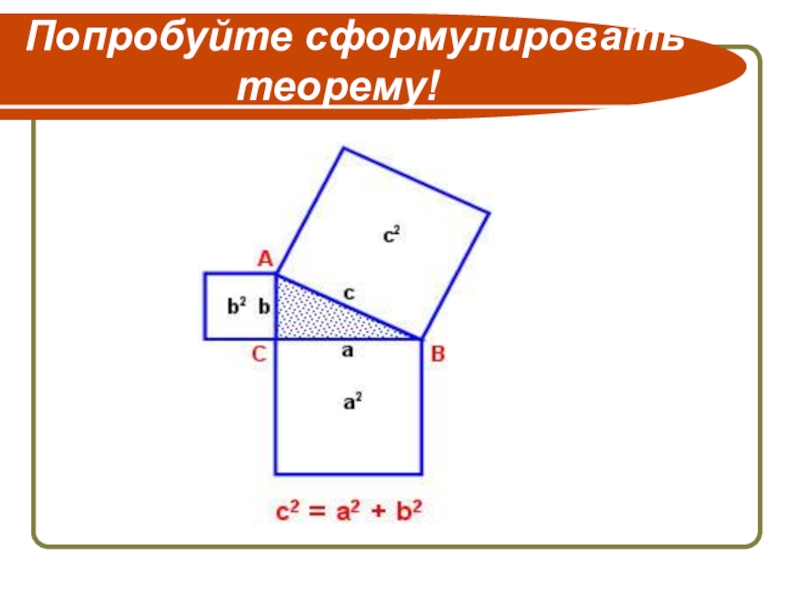
- 12. Попробуйте сформулировать теорему!
- 13. Так звучала теорема во времена ПифагораПлощадь квадрата
- 14. А так звучит современная формулировка: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
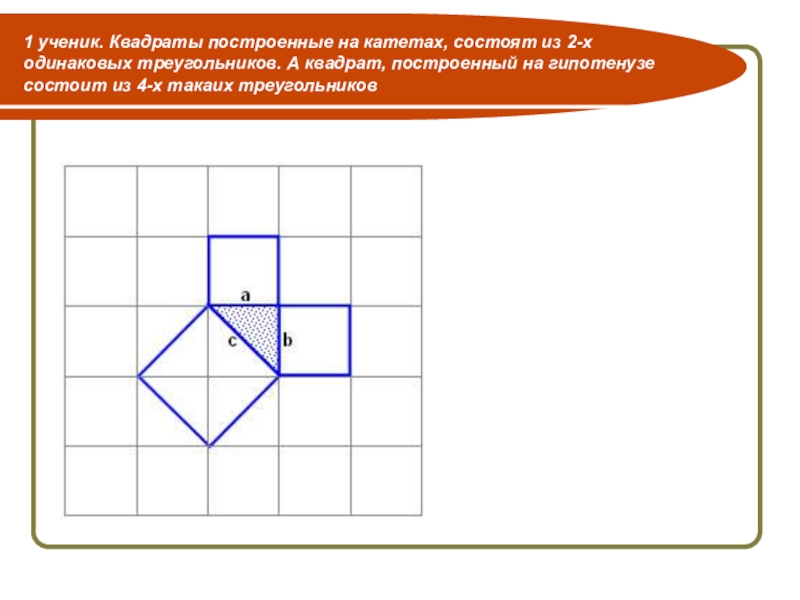
- 15. 1 ученик. Квадраты построенные на катетах, состоят
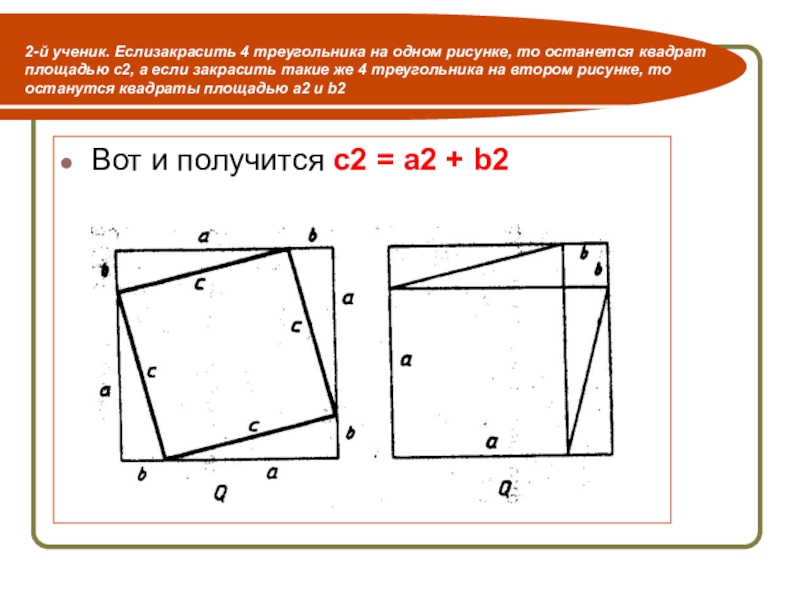
- 16. 2-й ученик. Еслизакрасить 4 треугольника на одном
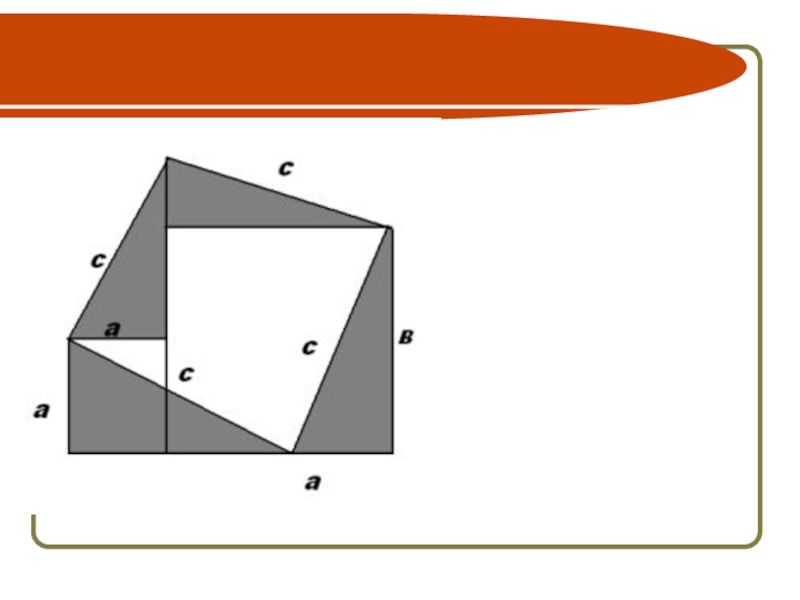
- 17. 3-й ученикЯ использовал этот же прием,
- 18. Слайд 18
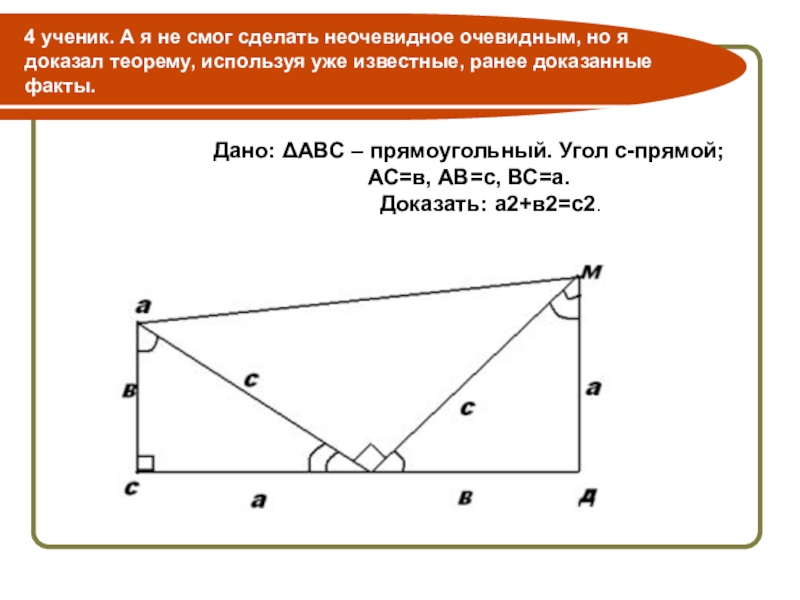
- 19. 4 ученик. А я не смог сделать
- 20. В чем достоинство этого способа доказательства?Этот способ
- 21. А сейчас вернемся к нашей задачеНа обоих
- 22. Дано: АС=30, ВД=20, АВ=50.
- 23. Рассмотрим еще одну задачу, для решения которой
- 24. Слайд 24
- 25. Слайд 25
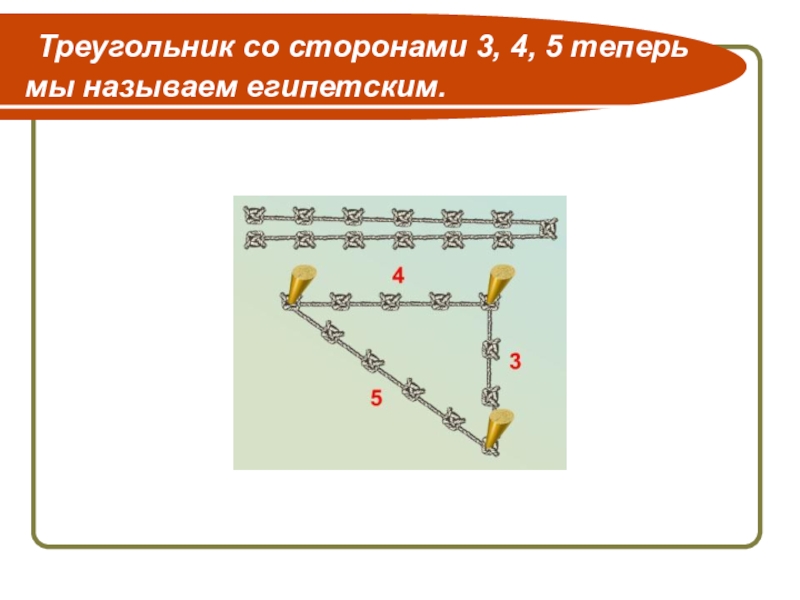
- 26. 4. Древние египтяне для построения прямоугольных треугольников
- 27. Треугольник со сторонами 3, 4, 5 теперь мы называем египетским.
- 28. Вам, наверное, известны также детские стишки о
- 29. До нас дошли и другие шуточные рисунки к теореме
- 30. Если дан нам треугольник И притом с
- 31. Спасибо за урок!
Старинная задачаНа обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно
Слайд 4Нужно знать зависимость между катетами и гипотенузой в прямоугольном треугольнике.
Эту зависимость
подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора.
Слайд 5Биография Пифагора
Пифагор-это не имя, а прозвище, данное ему
за
то , что он высказывал истину также постоянно, как дельфийский аракул, («Пифагор» значит «убеждающий речью») жил в Древней Греции. О жизни его известно немного, зато с именем его связан ряд легенд. Рассказывают, что он много путешествовал, изучал древнюю культуру и достижения науки разных стран.
то , что он высказывал истину также постоянно, как дельфийский аракул, («Пифагор» значит «убеждающий речью») жил в Древней Греции. О жизни его известно немного, зато с именем его связан ряд легенд. Рассказывают, что он много путешествовал, изучал древнюю культуру и достижения науки разных стран.
Слайд 6Пифагорейская школа
Вернувшись на родину, Пифагор
организовал кружок молодежи из
представителей аристократии. В
кружок принимались с большими
церемониями после долгих испытаний.
Каждый вступающий отрекался от
своего имущества и давал клятву
хранить в тайне учения основателя.
Так на юге Италии, которая была
тогда греческой колонией, возникла
пифагорейская школа.
представителей аристократии. В
кружок принимались с большими
церемониями после долгих испытаний.
Каждый вступающий отрекался от
своего имущества и давал клятву
хранить в тайне учения основателя.
Так на юге Италии, которая была
тогда греческой колонией, возникла
пифагорейская школа.
Слайд 7Пифагорейская школа
Пифагорейцы занимались
математикой, философией,
естественными науками.
Ими было сделано много важных открытий в арифметике и геометрии.
В школ существовал декрет, по которому авторство всех математических работ
приписывалось Пифагору.
естественными науками.
Ими было сделано много важных открытий в арифметике и геометрии.
В школ существовал декрет, по которому авторство всех математических работ
приписывалось Пифагору.
Звездчатый пятиугольник, или пентаграмма, - пифагорейский символ здравия и тайный опознавательный знак
Слайд 8 Заповеди Пифагора
и его учеников актуальны
и сейчас и могут быть
приемлемы для любого здравомыслящего человека.
Вот они!
приемлемы для любого здравомыслящего человека.
Вот они!
Слайд 9 Заповеди пифагорийцев
Делать то, что впоследствии не огорчит тебя
и не принудит раскаиваться;
Не делай никогда того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.
Не делай никогда того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.
Слайд 13Так звучала теорема во времена Пифагора
Площадь квадрата построенного на гипотенузе прямоугольного
треугольника равна сумме площадей квадратов, построенных на его катетах.
Слайд 14А так звучит современная формулировка:
В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов.
Слайд 151 ученик. Квадраты построенные на катетах, состоят из 2-х одинаковых треугольников.
А квадрат, построенный на гипотенузе состоит из 4-х такаих треугольников
Слайд 162-й ученик. Еслизакрасить 4 треугольника на одном рисунке, то останется квадрат
площадью с2, а если закрасить такие же 4 треугольника на втором рисунке, то останутся квадраты площадью a2 и b2
Вот и получится с2 = a2 + b2
Слайд 17 3-й ученик
Я использовал этот же прием, но по-другому. Поставил рядом
квадраты площадью a2 и b2. Теперь отрежем от них два одинаковых треугольника с катетами a и b и гипотенузой с, и переложим так, как показано на рисунке. Получим квадрат площадью с2 . Значит, опять получается, что a2+b2=c2.
Слайд 194 ученик. А я не смог сделать неочевидное очевидным, но я
доказал теорему, используя уже известные, ранее доказанные факты.
Дано: ΔАВС – прямоугольный. Угол с-прямой;
АС=в, АВ=с, ВС=а.
Доказать: а2+в2=с2.
Слайд 20В чем достоинство этого способа доказательства?
Этот способ доступен пониманию каждого, кто
занимается геометрией. Для того, чтобы его освоить, не надо обладать воображением или еще какими-то особенными способностями.
Слайд 21А сейчас вернемся к нашей задаче
На обоих берегах реки растет по
пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременною. На каком расстоянии от более высокой пальмы появилась раба.
Слайд 23Рассмотрим еще одну задачу, для решения которой нам необходимо знать теорему
Пифагора.
Над озером тихим,
С полфута размером,
Высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону.
Нет боле цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода глубока?
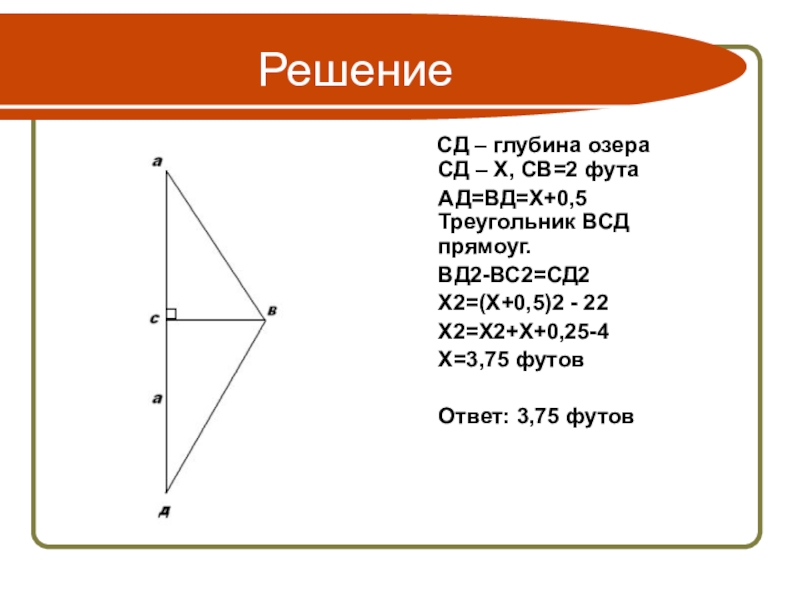
Слайд 24 Решение
СД – глубина озера СД – Х, СВ=2 фута
АД=ВД=Х+0,5 Треугольник ВСД прямоуг.
ВД2-ВС2=СД2
Х2=(Х+0,5)2 - 22
Х2=Х2+Х+0,25-4
Х=3,75 футов
Ответ: 3,75 футов
АД=ВД=Х+0,5 Треугольник ВСД прямоуг.
ВД2-ВС2=СД2
Х2=(Х+0,5)2 - 22
Х2=Х2+Х+0,25-4
Х=3,75 футов
Ответ: 3,75 футов
Слайд 25 Итог.
1.
Возможно было решение задач данного типа без знания теоремы Пифагора? Почему?
2. В чем суть теоремы Пифагора?
3. О чем надо помнить, применяя теорему Пифагора?
2. В чем суть теоремы Пифагора?
3. О чем надо помнить, применяя теорему Пифагора?
Слайд 264. Древние египтяне для построения прямоугольных треугольников пользовались веревкой с завязанными
на ней на одинаковых расстояниях узелками. По одной стороне они откладывали 3 отрезка, на другой 4, а на третьей 5.
Правильно ли они поступали?
Правильно ли они поступали?
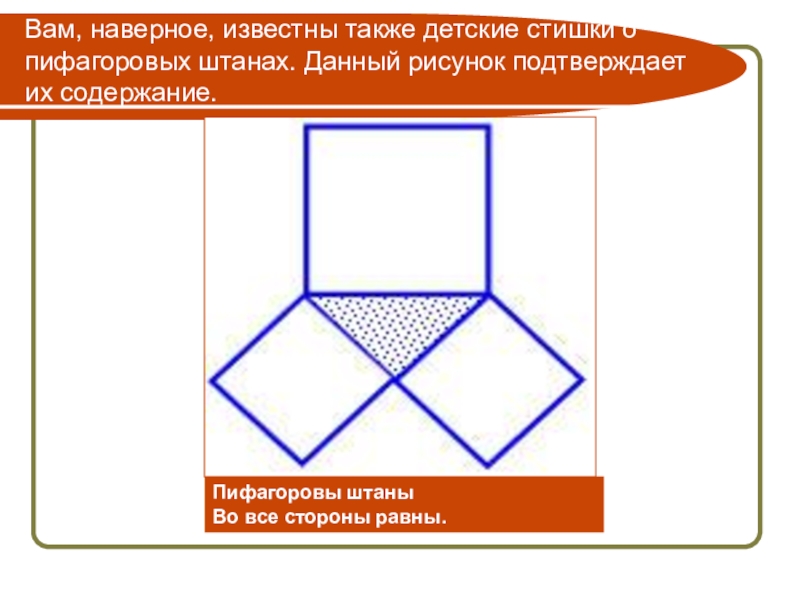
Слайд 28Вам, наверное, известны также детские стишки о пифагоровых штанах. Данный рисунок
подтверждает их содержание.
Пифагоровы штаны
Во все стороны равны.
Слайд 30
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путём
К результату мы придём.
