- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему тела вращения (11 класс)
Содержание
- 1. Презентация по геометрии на тему тела вращения (11 класс)
- 2. Содержание:Часть l :Тела вращения.Комбинации тел вращения.Часть ll :
- 3. Часть lТела вращения
- 4. Тела вращения Цилиндр.Конус. Шар. Исторические сведения.Проверь себя
- 5. Стереометрия - это раздел геометрии, в котором изучаются свойства фигур в пространстве.στερεοζμετρεμпространственныйизмерять
- 6. Исторические сведенияСтереометрия возникла и развивалась в связи
- 7. Тела вращенияФигура вращения получается в результате вращения
- 8. Тела вращения: Цилиндр Конус Шар ,(сфера)
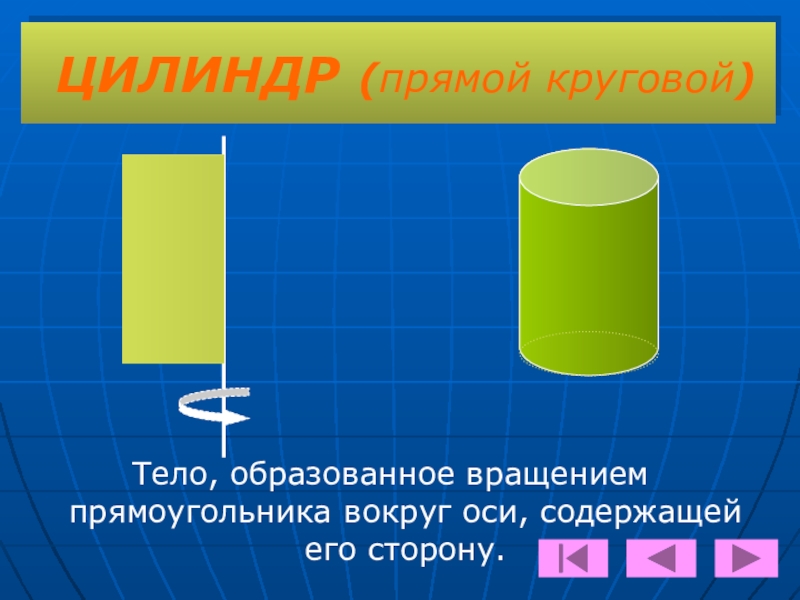
- 9. ЦИЛИНДР (прямой круговой)Тело, образованное вращением прямоугольника вокруг оси, содержащей его сторону.
- 10. КОНУС (прямой круговой) Тело, образованное вращением прямоугольного треугольника вокруг оси, содержащей его катет.
- 11. ШАРТело, образованное вращением полукруга вокруг оси, содержащей его диаметр.Дополнительные сведения
- 12. Шар радиуса R с центром в
- 13. Сфера Сферой называется поверхность, состоящая из всех
- 14. Дополнительные сведения Отрезок,соединяющий две точки сферы
- 15. ПРОВЕРЬ СЕБЯЧто изучает стереометрия?
- 16. Подсказка Стереометрия - это раздел геометрии, в котором изучаются свойства фигур в пространстве.
- 17. Что означает термин «стереометрия»?
- 18. подсказкаΣτερεοζ – пространственныйΜετρεμ - измерять
- 19. Какие фигуры в пространстве называются фигурами вращения?
- 20. подсказкаФигура вращения получается в результате вращения плоской
- 21. Приведите примеры фигур вращения.
- 22. Какая фигура получается при вращении прямоугольника вокруг оси, содержащей его сторону?
- 23. Какая фигура получается при вращении прямоугольного треугольника вокруг оси, содержащей его катет?
- 24. Какая фигура получается при вращении полукруга вокруг оси, содержащей его диаметр?
- 25. Чем отличается шар от сферы?
- 26. Справочные сведения
- 27. ( ЦИЛИНДР И
- 28. Подсказка4м.3м.?
- 29. ОТВЕТ: Задача 1): 5м.
- 30. 2)Осевое сечение цилиндра –квадрат, площадь которого S.Найдите площадь основания.Sкв. = Sответ
- 31. подсказкаSосн.= Sкр.= πr 2
- 32. ОТВЕТ:Задача 2): π• S/ 4.
- 33. 3)Высота цилиндра 6см.,радиус основания 5см. Найти площадь сечения, проведённого параллельно оси цилиндра на расстоянии 4см.от неё.R=5см.h=6см.ОО1Ответ
- 34. Подсказка
- 35. ОТВЕТ:Задача 3): 36 см2.
- 36. Справочные сведенияКОНУСОснование конусаОсь конусавершинаL- образующаяR-радиусоо1АВSбок. = πRLSкон.
- 37. УСТНЫЕ ЗАДАЧИ
- 38. Подсказка
- 39. Ответ: 5м .
- 40. 2)Образующая конуса L наклонена к плоскости основания под углом в 300. Найти высоту.ответ
- 41. Подсказка
- 42. Ответ: ½ • L .
- 43. 3)Радиус основания конуса R.Осевым сечением служит прямоугольный треугольник. Найти его площадь. ответ
- 44. Подсказка
- 45. Ответ:R2
- 46. Справочные сведения
- 47. УСТНЫЕ ЗАДАЧИ ( ШАР И
- 48. ПодсказкаV = 4 /3• πR3R=1м.О
- 49. Ответ: 4/3 • π ≈ 4,2 м3.
- 50. 2)Во сколько раз увеличится объём шара, если радиус его увеличить в 3 раза? ответ
- 51. ПодсказкаV = 4 /3• πR3R1RR1=3R
- 52. Ответ: в 27 раз.
- 53. Решение более сложных задач.
- 54. Задача 1: Высота и образующая конуса относятся
- 55. 1.Обозначим одну часть за х , тогда
- 56. Найдём радиус ОВ:
- 57. 3. т.к. R=ОВ=12х ,
- 58. Ответ: 1680π .
- 59. Задачи для самостоятельного решения.
- 60. Задача : Конусообразная палатка высотой в
- 61. ПодсказкаSбок. = πRL D=2R
- 62. Ответ: ≈ 25,3м2.
- 63. Задача : Боковая поверхность конуса
- 64. ПодсказкаVкон. = 1/3• πR2hSбок. = πRL∆ АОВ ~ ∆ АСОПропорция:
- 65. Ответ: 16см3
- 66. Задача: Боковая поверхность цилиндра будучи
- 67. ПодсказкаИз прямоугольного ∆АВD:Н=АВ = ВDsinφ= вsinφ,АD
- 68. Ответ:
- 69. Задача: Шар пересечён плоскостью, перпендикулярной
- 70. Подсказка Пусть ОВ = х –радиус сферы.
- 71. Ответ:V = 4500π см3;S = 900 π см2.
- 72. Задача: Определить площадь полной поверхности
- 73. подсказкаПо условию задачи:S = 2πRH, но
- 74. Ответ:Sполн.
- 75. Задача: Доказать ,что объём конуса равен
- 76. Задача: Даны шар, цилиндр с квадратным
- 77. Ответ: Vц.:Vш.:Vк.= 3:2:1
- 78. Задача: Равносторонний треугольник вращается
- 79. Подсказка При вращении получается два конуса
- 80. Ответ:
- 81. Задача: Равнобедренняй треугольник вращается вокруг своей
- 82. Подсказка При вращении этого треугольника вокруг высоты АС лучается конус.
- 83. Ответ: 11см., 11см., 8 см.
- 84. Часть llКомбинации тел вращения.
- 85. Комбинация тел вращенияКомбинация цилиндра и конуса;Комбинация цилиндра
- 86. Комбинация цилиндра и конуса Цилиндр называется вписанным
- 87. Комбинация цилиндра и конуса Конус называется вписанным
- 88. Комбинация цилиндра и шара Шар называется
- 89. Дополнительные сведения Центр шара лежит на оси
- 90. Комбинация цилиндра и шара Шар называется
- 91. Центром описанного около цилиндра, шара является середина оси цилиндра-отрезка, соединяющего центры его оснований. Дополнительные сведения
- 92. Комбинация конуса и шара Шар называется
- 93. Дополнительные сведения Шар касается боковой поверхности конуса по окружности, плоскость которой параллельна основанию. Дополнительные сведения
- 94. Центр шара, вписанного в конус,лежит
- 95. Комбинация конуса и шара Шар называется
- 96. Дополнительные сведения Центром шара, описанного около
- 97. Проверь себя
- 98. Введите понятие «цилиндр вписан в конус» и «конус вписан в цилиндр».
- 99. Введите понятие «конус вписан в шар» и «конус описан около шара».
- 100. Как расположены точки общие для шара и поверхности конуса?
- 101. Где расположен центр шара относительно вписанного конуса,что представляет осевое сечение данной комбинации фигур?
- 102. Где находится центр шара, вписанного в конус?
- 103. Центр шара, вписанного в конус,лежит
- 104. Укажите пары подобных треугольников и в них пары углов, имеющие равные величины?
- 105. Во всякий ли цилиндр можно вписать
- 106. подсказка Нет не во всякий: осевое сечение цилиндра должно быть квадратом.
- 107. Во всякий ли конус можно вписать сферу? Как определить положеное центра сферы, вписанной в конус?
- 108. подсказка Да, во всякий.Центр вписанной сферы находится
- 109. По известному радиусу основания конуса R и его высоте h найдите радиус вписанной сферы. подсказка
- 110. Подсказка: Искомый радиус : r = R·tgφ
- 111. Задачи для самостоятельного решения.
- 112. Задача: В конусе высотой 12см. вписан шар радиуса 3см. Вычислить объём конуса. ответ
- 113. Ответ: 72π см3.
- 114. Задача: В конус вписан цилиндр,
- 115. подсказка Пусть: R- радиус основания
- 116. Ответ : β = arctg
- 117. Доказать ,что отношение объёма конуса
- 118. Задача Определить боковую поверхность конуса, зная длину
- 119. Подсказка∆ АОВ - равнобедренный т.к. АО=ОВ=R.Проведём ОМ
- 120. Ответ: Sбок.= 2πR2sinβ·sinβ/2
- 121. Желаем удачи!
Содержание:Часть l :Тела вращения.Комбинации тел вращения.Часть ll :
Слайд 4Тела вращения
Цилиндр.
Конус.
Шар.
Исторические сведения.
Проверь себя ( теоретические сведения).
Решение
устных задач (ответы);
Задачи для самостоятельного решения,(подсказки, ответы).
Понятие о телах вращения
Слайд 5Стереометрия - это раздел геометрии, в котором изучаются свойства фигур в
пространстве.
στερεοζ
μετρεμ
пространственный
измерять
Слайд 6Исторические сведения
Стереометрия возникла и развивалась в связи с потребностями практической деятельности
человека.
Она зародилась в древнем Египте около 2000 лет до н. э., а оттуда перешла в Грецию.
Она зародилась в древнем Египте около 2000 лет до н. э., а оттуда перешла в Грецию.
Слайд 7Тела вращения
Фигура вращения получается в результате вращения плоской фигуры вокруг какой
- нибудь оси, лежащей в той же плоскости.
Слайд 9ЦИЛИНДР (прямой круговой)
Тело, образованное вращением прямоугольника вокруг оси, содержащей его сторону.
Слайд 10КОНУС (прямой круговой)
Тело, образованное вращением прямоугольного треугольника вокруг оси,
содержащей его катет.
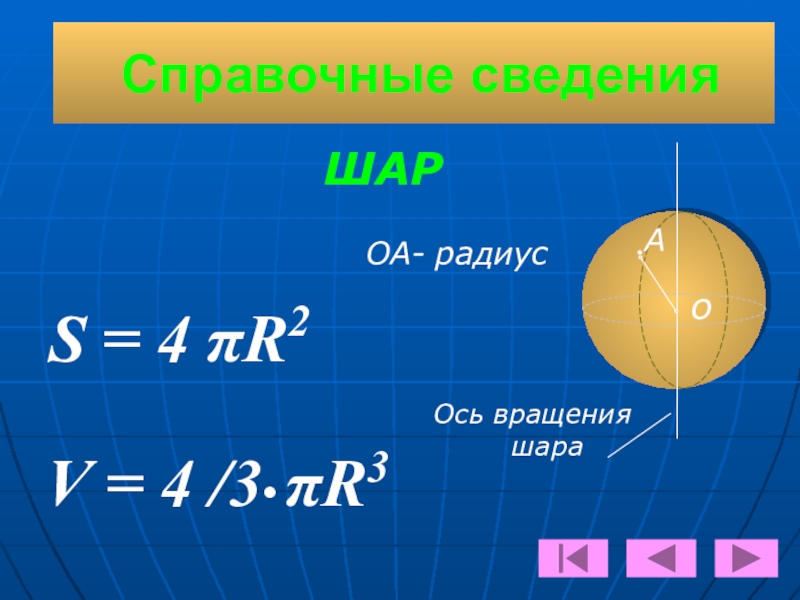
Слайд 11ШАР
Тело, образованное вращением полукруга вокруг оси, содержащей его диаметр.
Дополнительные сведения
Слайд 12 Шар радиуса R с центром в точке О содержит все
точки пространства, которые расположены от точки О на расстоянии не больше чем R (включая точку О), и не содержит других точек.
О
сфера
Слайд 13Сфера
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на
данном расстоянии R от данной точки О.
R
О
Радиус сферы
Центр сферы
Дополнительные сведения
Слайд 14Дополнительные сведения
Отрезок,соединяющий две точки сферы и проходящий через её
центр, называется её диаметром.
Диаметр сферы равен двум радиусам: D=2R.
Диаметр сферы равен двум радиусам: D=2R.
О
•
А
В
Слайд 16Подсказка
Стереометрия - это раздел геометрии, в котором изучаются свойства фигур
в пространстве.
Слайд 20подсказка
Фигура вращения получается в результате вращения плоской фигуры вокруг какой -
нибудь оси, лежащей в той же плоскости.
Слайд 23Какая фигура получается при вращении прямоугольного треугольника вокруг
оси, содержащей его катет?
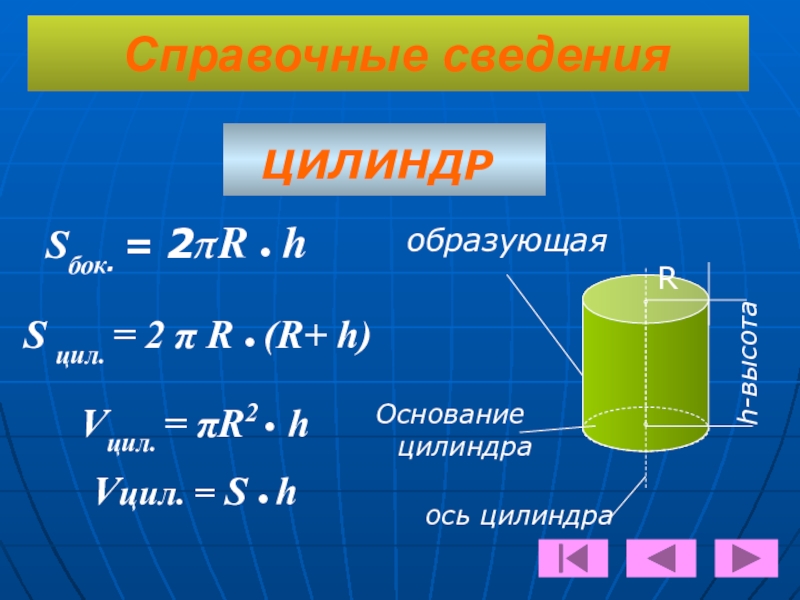
Слайд 26Справочные сведения
ЦИЛИНДР
образующая
ось цилиндра
Основание цилиндра
h-высота
R
Sбок.
= 2πR • h
S цил. = 2 π R • (R+ h)
Vцил. = πR2 • h
Vцил. = S • h
Слайд 27 ( ЦИЛИНДР И ЕГО СВОЙСТВА)
УСТНЫЕ ЗАДАЧИ
1)Радиус основания
цилиндра 2м.,высота 3м.Найти диагональ осевого сечения.
h=3м.
О1
R=2м.
.
ответ
Слайд 302)Осевое сечение цилиндра –квадрат, площадь которого S.Найдите площадь основания.
Sкв. = S
ответ
Слайд 333)Высота цилиндра 6см.,радиус основания 5см. Найти площадь сечения, проведённого параллельно оси
цилиндра на расстоянии 4см.от неё.
R=5см.
h=6см.
О
О1
Ответ
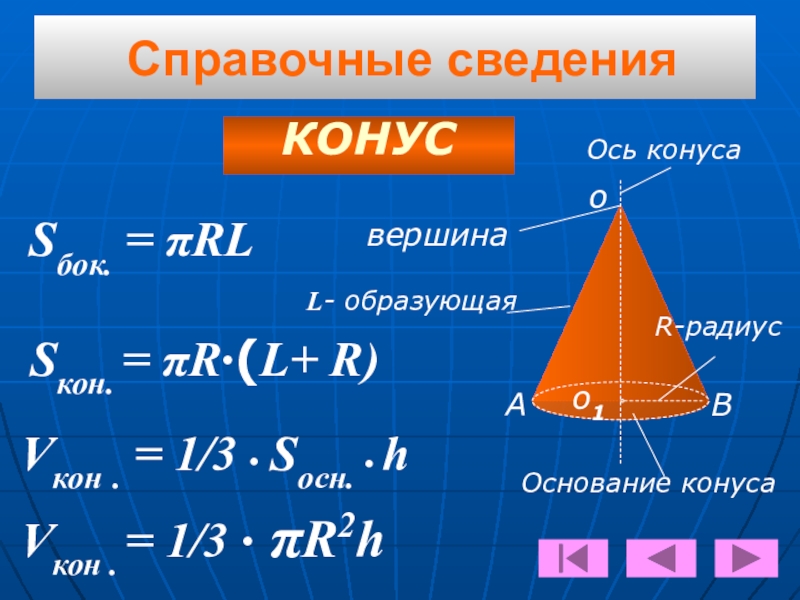
Слайд 36Справочные сведения
КОНУС
Основание конуса
Ось конуса
вершина
L- образующая
R-радиус
о
о1
А
В
Sбок. = πRL
Sкон. = πR•(L+ R)
Vкон
. = 1/3 • πR2h
Vкон . = 1/3 • Sосн. • h
Слайд 43 3)Радиус основания конуса R.Осевым сечением служит прямоугольный треугольник. Найти его
площадь.
ответ
Слайд 54Задача 1: Высота и образующая конуса относятся как 35:37. Полная поверхность
конуса равна 588π. Найти объём конуса.
решение
ответ
Слайд 551.Обозначим одну часть за х , тогда образующая l = 37х
, а высота h = 35х. Рассм . ∆АОВ :
Дано:
конус
h:l=35:37
Sкон.=588π
Найти:Vкон.
Решение:
L АОВ=90 0, АО=h, АВ=l , ОВ=R.
Слайд 56Найдём радиус ОВ:
ОВ2 =
АВ2 - АО2, значит
ОВ = √(37х)2-( 35х)2 = 12х ;
ОВ = √(37х)2-( 35х)2 = 12х ;
___________
2.Теперь найдём Sкон. т.е. полную поверхность конуса (через х):
Sкон. = S осн . + Sбок.
Sкон. = π R2+ π R l
Sкон. = π(144х2+444х2)
588π = 588πх2
х=1.
Слайд 573. т.к. R=ОВ=12х ,
то R
= 12; а т.к. h = АО = 35х , то h = 35.
4. Найдём объём конуса:
V = ⅓* π R2* h
V = ⅓* π * 144 *35= 1680 π .
Ответ: 1680 π .
4. Найдём объём конуса:
V = ⅓* π R2* h
V = ⅓* π * 144 *35= 1680 π .
Ответ: 1680 π .
А
Слайд 60
Задача :
Конусообразная палатка высотой в 3,5 м. с диаметром
основания в 4м. покрыта парусиной. Сколько квадратных метров парусины пошло на палатку?
ответ
Слайд 63
Задача :
Боковая поверхность конуса 12 см2., расстояние от
центра основания конуса до образующей 4см. Определить объём конуса.
ответ
Слайд 66
Задача:
Боковая поверхность цилиндра будучи развёрнута, представляет собой
прямоугольник. В котором диагональ равна в и составляет угол φ с основанием. Найти объём цилиндра?
ответ
Слайд 67Подсказка
Из прямоугольного ∆АВD:
Н=АВ = ВDsinφ= вsinφ,
АD = ВDcosφ= вcosφ.
но, сторона
АD равна длине окружности основания,
т.е. 2πR = вcos φ,
отсюда найдём R.
т.е. 2πR = вcos φ,
отсюда найдём R.
Слайд 69
Задача:
Шар пересечён плоскостью, перпендикулярной его радиусу и отстоящей
от его центра на 9 см. Площадь сечения равна 144 π см2.
Найти объём шара и площадь сферы.
Найти объём шара и площадь сферы.
ответ
Слайд 70Подсказка
Пусть ОВ = х –радиус сферы.
В ∆
ОАВ :
АВ2= ОВ2- ОА2= х2- 81.
По условию: πR2=144 π,
значит:
π (х2 – 81) = 144 π и т. д.
АВ2= ОВ2- ОА2= х2- 81.
По условию: πR2=144 π,
значит:
π (х2 – 81) = 144 π и т. д.
Слайд 72
Задача:
Определить площадь полной поверхности и объём цилиндра,осевое сечение
которого есть квадрат и боковая поверхность равна S.
ответ
Слайд 75 Задача:
Доказать ,что объём конуса равен 1/3 произведения боковой поверхности
на расстояние от центра основания до образующей.
Слайд 76Задача:
Даны шар, цилиндр с квадратным осевым сечением и
конус.Цилиндр и конус имеют одинаковые основания, а их высоты равны диаметру шара.Как относятся объёмы цилиндра, шара и конуса?
ответ
Слайд 78Задача:
Равносторонний треугольник вращается вокруг своей
стороны а. Найти поверхность и объём тела вращения.
а
подсказка
ответ
Слайд 79Подсказка
При вращении получается два конуса с радиусом основания ОВ.
Поверхность тела вращения – это две одинаковые боковые поверхности указанного конуса.
Слайд 81 Задача:
Равнобедренняй треугольник вращается вокруг своей высоты. Определить стороны этого
треугольника, если его периметр равен 30 см., а полная поверхность тела вращения равна 60π см2.
подсказка
ответ
Слайд 85Комбинация тел вращения
Комбинация цилиндра и конуса;
Комбинация цилиндра и шара;
Комбинация конуса и
шара.
Основные понятия о комбинации тел вращения:
Проверь себя (теоретические сведения).
Задачи для самостоятельного решения, (ответы).
Слайд 86Комбинация цилиндра и конуса
Цилиндр называется вписанным в конус, если окружность
одного из его оснований лежит на поверхности конуса, а другое основание расположено в плоскости основания конуса.
Слайд 87Комбинация цилиндра и конуса
Конус называется вписанным в цилиндр, если основание
конуса совпадает с одним из оснований цилиндра, а вершина конуса лежит в центре другого основания цилиндра.
Слайд 88Комбинация цилиндра и шара
Шар называется вписанным в цилиндр, если
основания и каждая образующая цилиндра касаются шара. В этом случае цилиндр называют описанным около шара.
Дополнительные сведения
Слайд 89Дополнительные сведения
Центр шара лежит на оси цилиндра, осевое сечение цилиндра
представляет собой квадрат со стороной, равной диаметру шара.
Слайд 90Комбинация цилиндра и шара
Шар называется описанным около цилиндра, если
основаниями цилиндра служат сечения шара. В этом случае цилиндр называют вписанным в шар.
дополнительные сведения
Слайд 91 Центром описанного около цилиндра, шара является середина оси цилиндра-отрезка, соединяющего
центры его оснований.
Дополнительные сведения
Слайд 92Комбинация конуса и шара
Шар называется вписанным в конус, если
основание и каждая образующая конуса касаются шара.В этом случае конус называется описанным около шара.
дополнительные сведения
Слайд 93Дополнительные сведения
Шар касается боковой поверхности конуса по окружности, плоскость
которой параллельна основанию.
Дополнительные сведения
Слайд 94 Центр шара, вписанного в конус,лежит в точке пересечения высоты
конуса и биссектрисы угла наклона образующей конуса к плоскости его основания.
Дополнительные сведения
Слайд 95Комбинация конуса и шара
Шар называется описанным около конуса, если
окружность основания и вершина, принадлежат поверхности конуса. В этом случае конус называют вписанным в шар.
дополнительные сведения
Слайд 96Дополнительные сведения
Центром шара, описанного около конуса, является точка пересечения
высоты конуса с перпендикуляром к образующей, проведённым через её середину в плоскости осевого сечения конуса.
Слайд 101 Где расположен центр шара относительно вписанного конуса,что представляет осевое
сечение данной комбинации фигур?
Слайд 103 Центр шара, вписанного в конус,лежит в точке пересечения высоты
конуса и биссектрисы угла наклона образующей конуса к плоскости его основания.
Подсказка
Слайд 105
Во всякий ли цилиндр можно вписать сферу? Какими свойствами
должен обладать цилиндр, чтобы в него можно было вписать сферу?
Слайд 107 Во всякий ли конус можно вписать сферу? Как определить положеное
центра сферы, вписанной в конус?
Слайд 108подсказка
Да, во всякий.Центр вписанной сферы находится на пересечении высоты конуса
и биссектрисы угла наклона образующей к плоскости основания.
Слайд 109 По известному радиусу основания конуса R и его высоте h
найдите радиус вписанной сферы.
подсказка
Слайд 110Подсказка:
Искомый радиус : r = R·tgφ , где φ- половина
угла наклона образующей конуса к плоскости основания, причём tg2φ=h:R .
Слайд 114 Задача:
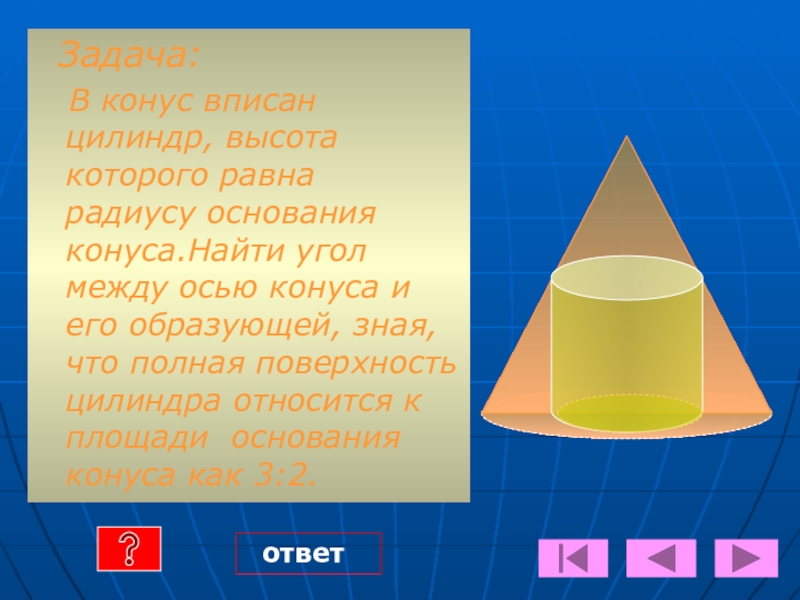
В конус вписан цилиндр, высота которого равна радиусу
основания конуса.Найти угол между осью конуса и его образующей, зная, что полная поверхность цилиндра относится к площади основания конуса как 3:2.
ответ
Слайд 115подсказка
Пусть:
R- радиус основания конуса,
r-радиус основания цилиндра,
β - искомый угол.
По условию ОВ=ОD=R.
β - искомый угол.
По условию ОВ=ОD=R.
Слайд 117 Доказать ,что отношение объёма конуса к объёму вписанного в
него шара равно отношению площади полной поверхности конуса к площади шоверхности шара.
Задача:
Слайд 118Задача
Определить боковую поверхность конуса, зная длину радиуса R, описанного вокруг
него шара и угол β, под которым из центра видна образующая конуса.
ответ
Слайд 119Подсказка
∆ АОВ - равнобедренный т.к. АО=ОВ=R.
Проведём ОМ – высоту.
Тогда ВМ= ½
• ВА= ½ ·L,
L ВОМ = ½ • β ,
Из ∆ ВОМ найдём ВМ:
ВМ = ОВ·sin β /2 , т. е.
½ ·L = R·sin β /2 ,
L=2R·sin β /2 .
L ВОМ = ½ • β ,
Из ∆ ВОМ найдём ВМ:
ВМ = ОВ·sin β /2 , т. е.
½ ·L = R·sin β /2 ,
L=2R·sin β /2 .
