- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Тангенс
Содержание
- 1. Презентация по геометрии на тему Тангенс
- 2. 03. 05. 18Классная работаТангенс
- 3. Мы уже познакомились с основами тригонометрии: с
- 4. Например, мы хотим по длине тени найти
- 5. Эта практическая задача в теории звучит так:
- 6. Отношение синуса и косинуса одного и того
- 7. Определение.Тангенсом угла называется отношение синуса угла к
- 8. Теперь решение рассмотренной задачи вместо равенства (1)
- 9. Формула (2)показывает, что тангенс прямого угла не
- 10. Значения тангенсов конкретных углов находят по таблицам
- 11. Свойства тангенса для острых углов легко увидеть,
- 12. Из этого рисунка ясно, что при увеличении
- 13. Решение задач№ 8.3; № 8.12; № 8.13 (а, б, в);№ 8. 20
- 14. № 8.3Расположите в порядкевозрастания тангенсы углов:а) 30°,
- 15. № 8.12
- 16. № 8.13 (а, б, в)
- 17. Домашнее заданиеn 8. 1№ 8.13 (г, д); № 8.16; № 8.17
03. 05. 18Классная работаТангенс
Слайд 3Мы уже познакомились с основами тригонометрии: с определениями
и свойствами первых двух тригонометрических функций — синуса и косинуса. Кроме них, применяют и другие тригонометрические функции. Они, естественно, возникают при решении даже совсем простых задач как в теории, так и на практике.
Слайд 4Например, мы хотим по длине тени найти высоту некоторого предмета, скажем,
дерева или вышки .
Угол, под которым виден этот предмет, мы измерить можем.
Угол, под которым виден этот предмет, мы измерить можем.
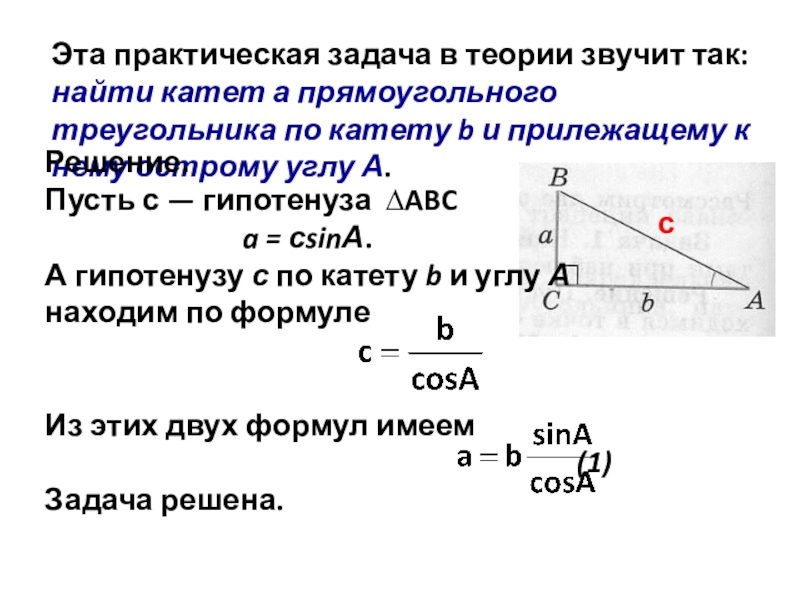
Слайд 5Эта практическая задача в теории звучит так: найти катет а прямоугольного
треугольника по катету b и прилежащему к нему острому углу А.
Решение.
Пусть с — гипотенуза ∆ABC
a = сsinА.
А гипотенузу с по катету b и углу А
находим по формуле
Из этих двух формул имеем
(1)
Задача решена.
с
Слайд 6Отношение синуса и косинуса одного и того же угла
появляется и
при решении других задач.
Поэтому удобно ввести ещё одну тригонометрическую функцию угла, которая равна отношению синуса и косинуса этого угла.
Поэтому удобно ввести ещё одну тригонометрическую функцию угла, которая равна отношению синуса и косинуса этого угла.
Слайд 7Определение.
Тангенсом угла называется отношение синуса угла к его косинусу.
Эту функцию
обозначают символом tg .
Итак, тангенс угла А определяется равенством
Итак, тангенс угла А определяется равенством
(2)
Слайд 8Теперь решение рассмотренной задачи вместо равенства (1)
может быть записано в
таком виде:
Таким образом, тангенс острого угла прямоугольного треугольника равен отношению катета, противолежащего этому углу, к катету, прилежащему к этому углу, т. е.
Таким образом, тангенс острого угла прямоугольного треугольника равен отношению катета, противолежащего этому углу, к катету, прилежащему к этому углу, т. е.
Короче говорят так: тангенс равен отношению противолежащего катета к прилежащему катету.
(4)
(3)
Слайд 9Формула (2)
показывает, что тангенс прямого угла не определён (поскольку знаменатель в
правой части равенства (2) для прямого угла А обращается в нуль).
Как синус и косинус, тангенс является функцией величины угла. Поэтому пишем
tg 43°, tg78° и т. п.
Как синус и косинус, тангенс является функцией величины угла. Поэтому пишем
tg 43°, tg78° и т. п.
Слайд 10Значения тангенсов конкретных углов находят по таблицам или с помощью калькулятора.
Так
как
sin (180° - α) = sin α и cos (180° - α) = - cos α,
то
tg(180° - α) = - tg α
Это равенство связывает тангенсы смежных углов.
sin (180° - α) = sin α и cos (180° - α) = - cos α,
то
tg(180° - α) = - tg α
Это равенство связывает тангенсы смежных углов.
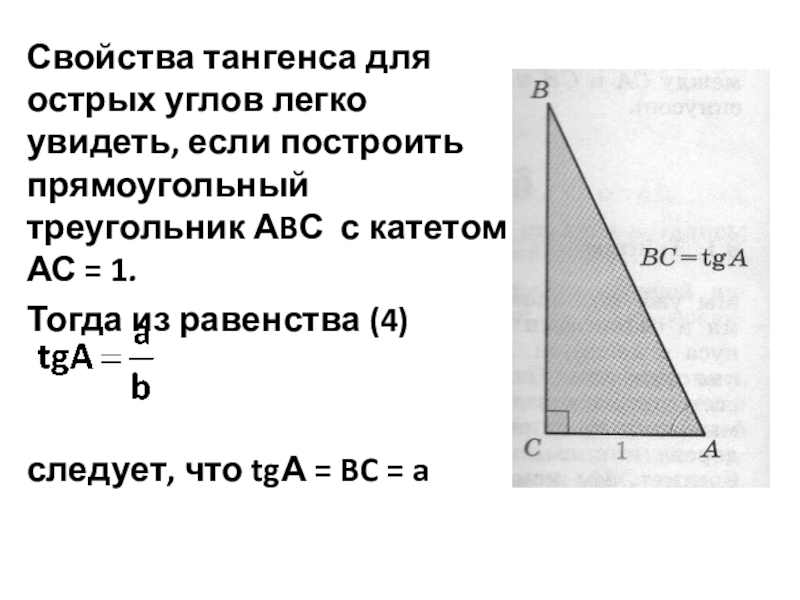
Слайд 11Свойства тангенса для острых углов легко увидеть, если построить прямоугольный треугольник
АBС с катетом АС = 1.
Тогда из равенства (4)
следует, что tgА = BC = a
Тогда из равенства (4)
следует, что tgА = BC = a
Слайд 12Из этого рисунка ясно,
что при увеличении угла
от 0° до
90° тангенс возрастает от нуля до бесконечности.
Поэтому для острых углов тангенс определяет угол.
График тангенса приведён
на рис.
Поэтому для острых углов тангенс определяет угол.
График тангенса приведён
на рис.
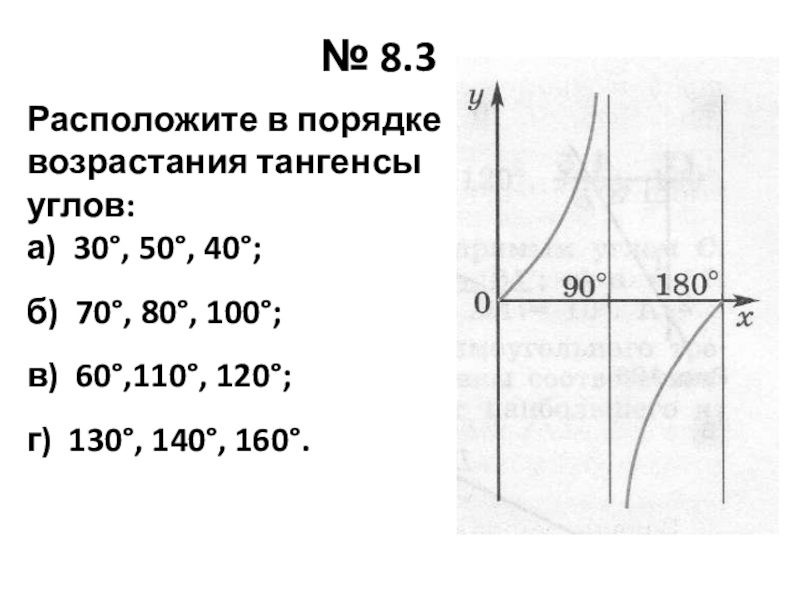
Слайд 14№ 8.3
Расположите в порядке
возрастания тангенсы углов:
а) 30°, 50°, 40°;
б) 70°, 80°,
100°;
в) 60°,110°, 120°;
г) 130°, 140°, 160°.
в) 60°,110°, 120°;
г) 130°, 140°, 160°.