- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему стереометрия
Содержание
- 1. Презентация по геометрии на тему стереометрия
- 2. ПирамидаЭто многогранник, основание которого-многоугольник, а остальные грани-треугольники,
- 3. ПризмаЭто многогранник у которого две грани являются
- 4. Параллелепипед-это четырехугольная призма основаниями которой являются параллеграммы.
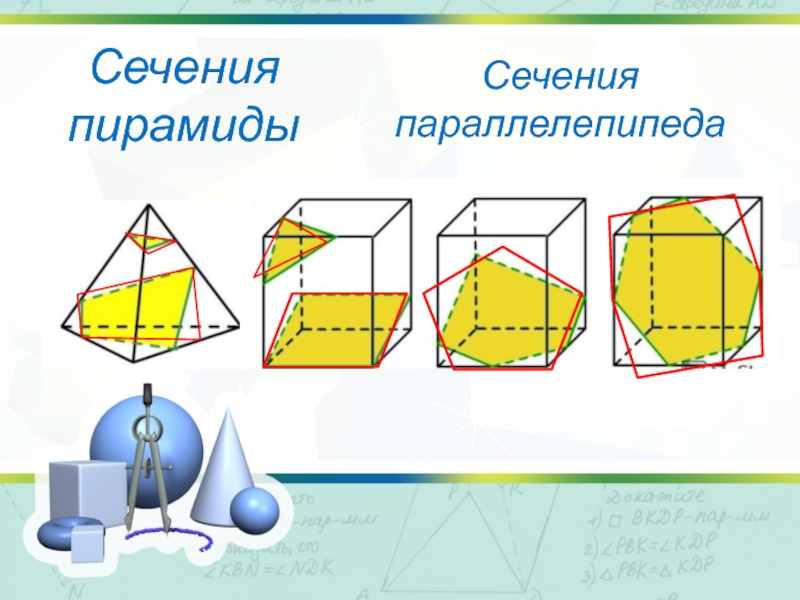
- 5. Сечения пирамидыСечения параллелепипеда
- 6. «тетра» «гекса»
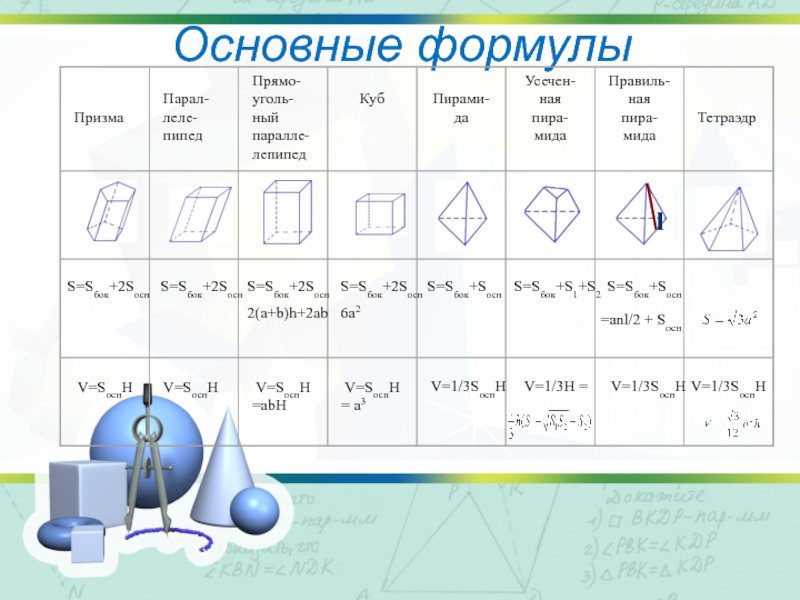
- 7. Основные формулыS=Sбок+2SоснS=Sбок+2SоснS=Sбок+2Sосн2(a+b)h+2abS=Sбок+2Sосн6a2S=Sбок+SоснS=Sбок+SоснS=Sбок+S1+S2 V=1/3SоснH V=1/3H = V=1/3SоснH V=1/3SоснH=anl/2 + Sосн
- 8. Порешаем задачи:
- 9. Задача.Сколько кубиков с ребром 3 см можно
- 10. Задача. Сколько кг краски потребуется для покраски
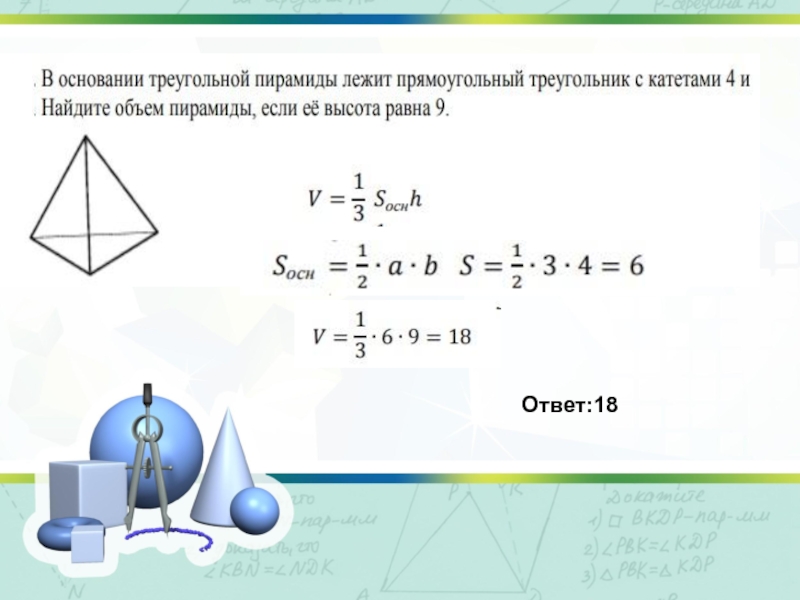
- 11. Ответ:18
- 12. Основание пирамиды является параллелограмм со сторонами 5м
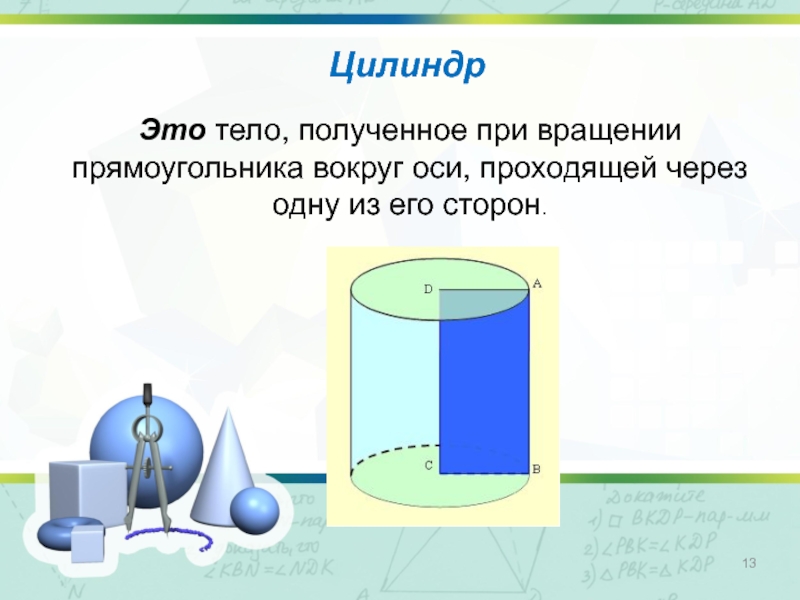
- 13. ЦилиндрЭто тело, полученное при вращении прямоугольника вокруг оси, проходящей через одну из его сторон.
- 14. Основаниями цилиндра называются круги, полученные в результате
- 15. Основные свойства Основания цилиндра равны и лежат
- 16. Сечения цилиндраСечение цилиндра плоскостью, проходящей через ось
- 17. Основные формулы: R - радиус основания; H
- 18. КонусЭто тело, полученное при вращении прямоугольного треугольника вокруг оси, содержащей его катет.
- 19. Вершиной конуса называется точка, не лежащая в
- 20. Основные свойстваПолная поверхность конуса состоит из основания
- 21. Сечения конусаСечение конуса плоскостью, проходящей через его
- 22. Основные формулыR - радиус основания; Н –
- 23. Усеченный конусЭто часть конуса, заключенная между его основанием и секущей плоскостью, параллельной плоскости основания конуса.
- 24. Основные определенияОснованиями усеченного конуса называются основание данного
- 25. УСЕЧЕННЫЙ КОНУС: основные свойстваВсе образующие усеченного
- 26. Некоторые варианты сечений усеченного конусаНLRНLRСечение усеченного конуса
- 27. Основные формулы:R и r - радиусы оснований;
- 28. Сфера и шар Шаром называется тело,
- 29. Шаром называется тело, которое состоит из всех
- 30. Плоскость, проходящая через центр шара, называется диаметральной
- 31. Сфера и шар: R - сферы; d - диаметрПлощадь поверхности сферы: Объем шара: RRRdORОбъем шара: RRRdOR
- 32. Формулы площади поверхности и объема тел вращения
- 33. Порешаем задачи:
- 34. Задача 1. Токарю надо выточить деталь в
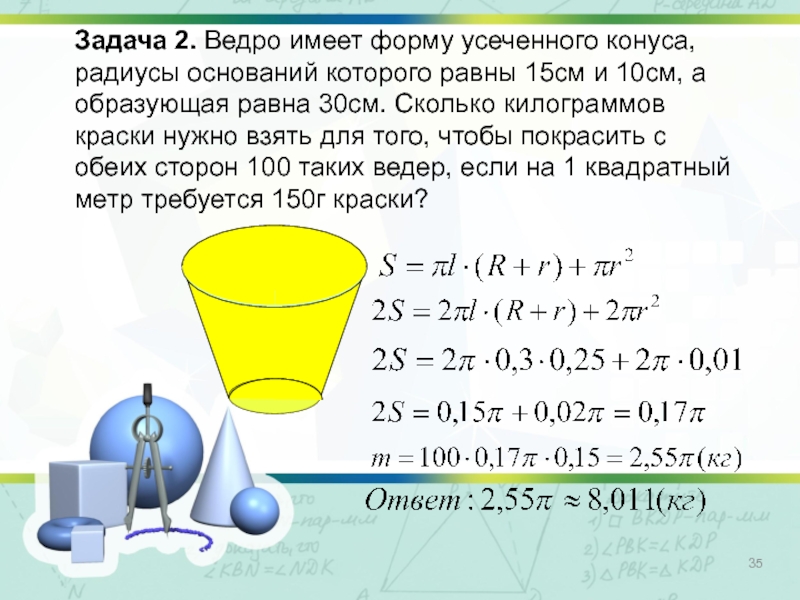
- 35. Задача 2. Ведро имеет форму усеченного конуса,
- 36. Задача Сколько кожи пойдет на покрытие футбольного
- 37. Задача Сколько квадратных метров листовой жести пойдет
- 38. Задача Стаканчик для мороженого конической формы имеет
- 39. Спасибо за внимание!
Слайд 1Стереометрия
Маслова И.Н.
учитель математики
МОУ «СОШ № 21»
г. Подольска
9 класс
И
Многогранники
Тела вращения
Слайд 2Пирамида
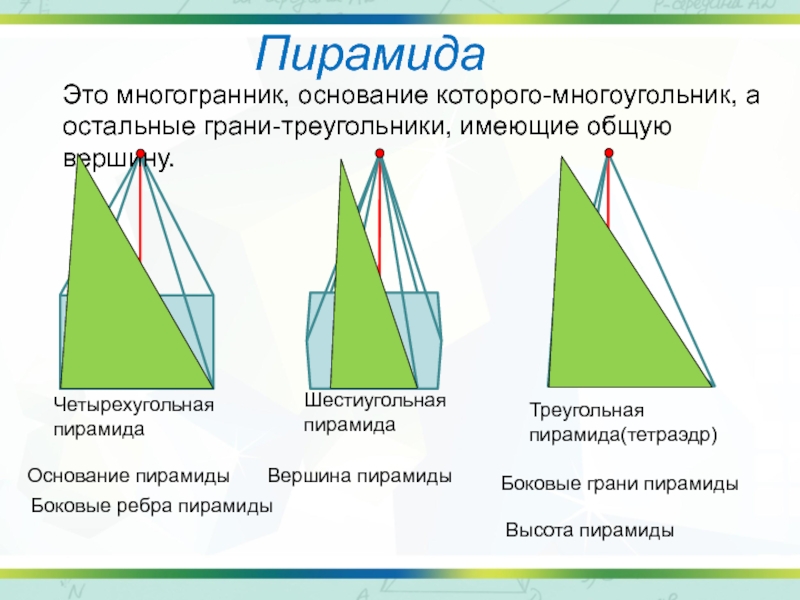
Это многогранник, основание которого-многоугольник, а остальные грани-треугольники, имеющие общую вершину.
Четырехугольная пирамида
Шестиугольная
Треугольная пирамида(тетраэдр)
Основание пирамиды
Боковые ребра пирамиды
Высота пирамиды
Боковые грани пирамиды
Вершина пирамиды
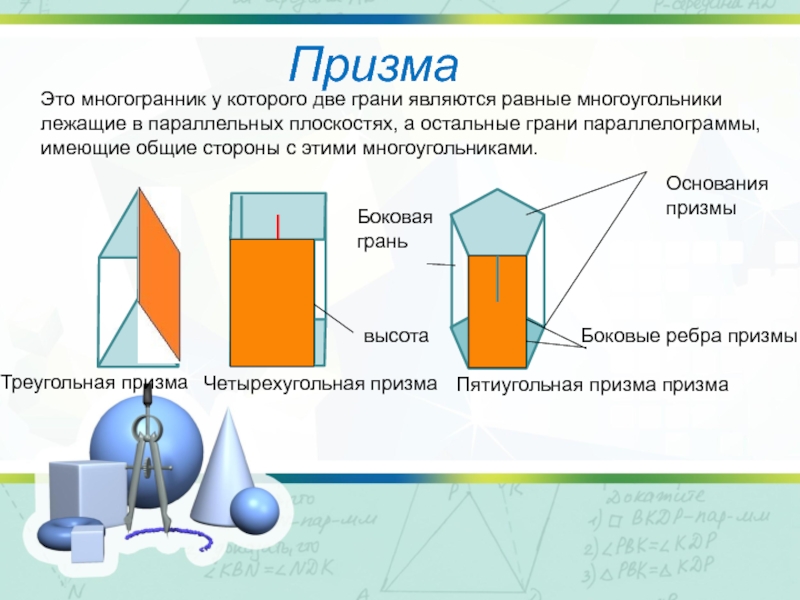
Слайд 3Призма
Это многогранник у которого две грани являются равные многоугольники лежащие в
Четырехугольная призма
Пятиугольная призма призма
Треугольная призма
Основания призмы
Боковые ребра призмы
Боковая грань
высота
Слайд 4Параллелепипед-это четырехугольная призма основаниями которой являются параллеграммы.
Призмы бывают :
наклонные
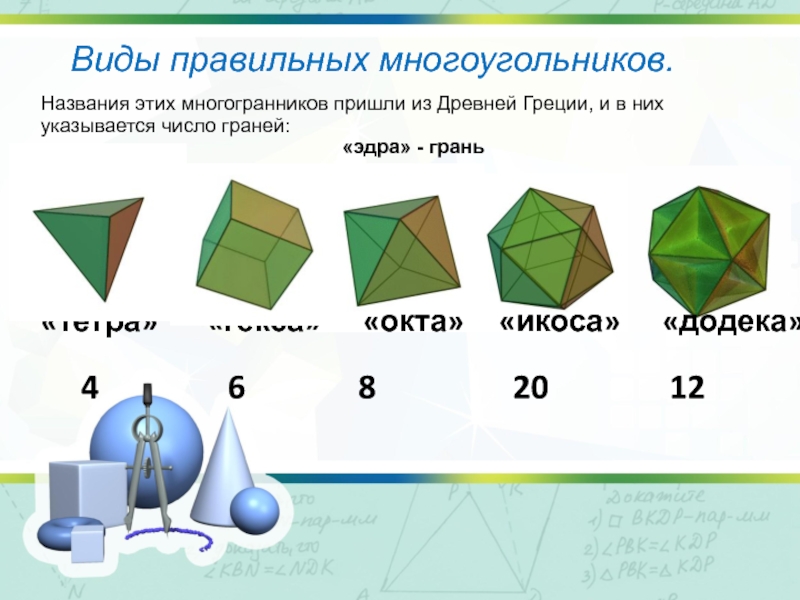
Слайд 6«тетра» «гекса» «окта» «икоса»
4 6 8 20 12
Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:
«эдра» - грань
Виды правильных многоугольников.
Слайд 7Основные формулы
S=Sбок+2Sосн
S=Sбок+2Sосн
S=Sбок+2Sосн
2(a+b)h+2ab
S=Sбок+2Sосн
6a2
S=Sбок+Sосн
S=Sбок+Sосн
S=Sбок+S1+S2
V=1/3SоснH
V=1/3H =
V=1/3SоснH
V=1/3SоснH
=anl/2 + Sосн
Слайд 9Задача.Сколько кубиков с ребром 3 см можно выплавить из свинцового бруска
Дано: параллелепипед,
а=10 см, b=7 см, h =2 см ,
Куб с=3см
Найти: n
Решение
V₁=a*b*h=10*7*2=140 cм³
V₂=a³=27
n= V₁/ V₂≈5
Ответ:5
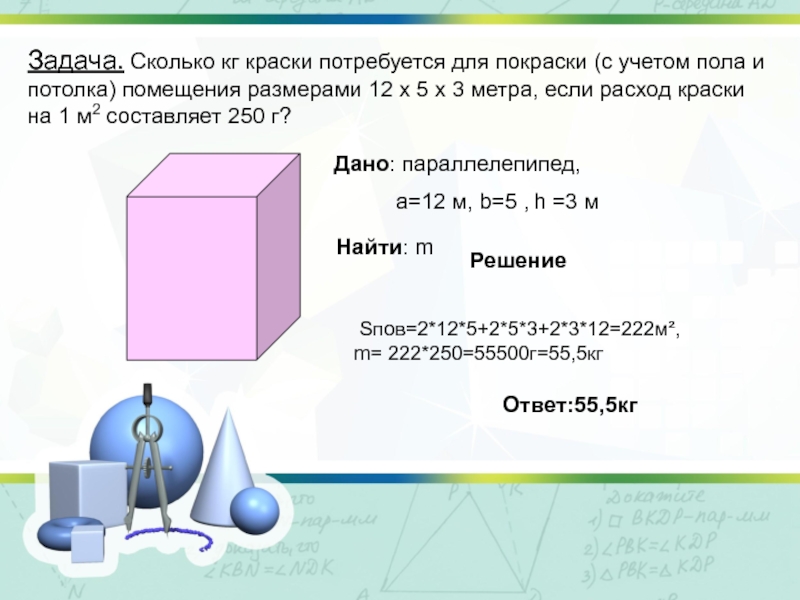
Слайд 10Задача. Сколько кг краски потребуется для покраски (с учетом пола и
Дано: параллелепипед,
а=12 м, b=5 , h =3 м
Найти: m
Решение
Sпов=2*12*5+2*5*3+2*3*12=222м²,
m= 222*250=55500г=55,5кг
Ответ:55,5кг
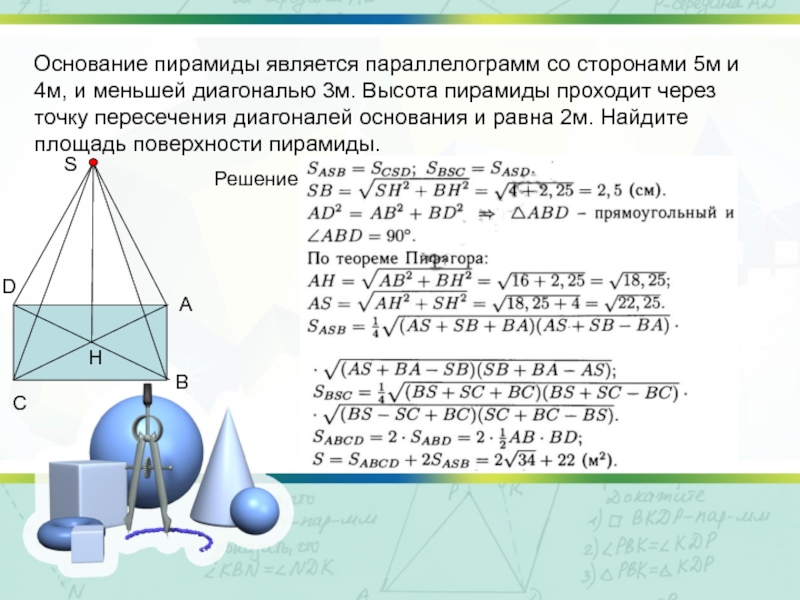
Слайд 12Основание пирамиды является параллелограмм со сторонами 5м и 4м, и меньшей
Решение:
А
С
В
D
S
H
Слайд 13Цилиндр
Это тело, полученное при вращении прямоугольника вокруг оси, проходящей через одну
Слайд 14
Основаниями цилиндра называются круги, полученные в результате вращения сторон прямоугольника, смежных
Образующими цилиндра называются отрезки, соединяющие соответствующие точки окружностей кругов.
Радиусом цилиндра называется радиус его основания.
Высотой цилиндра называется расстояние между плоскостями оснований.
Осью цилиндра называется прямая, проходящая через центры оснований.
Н
R
O
O1
Слайд 15
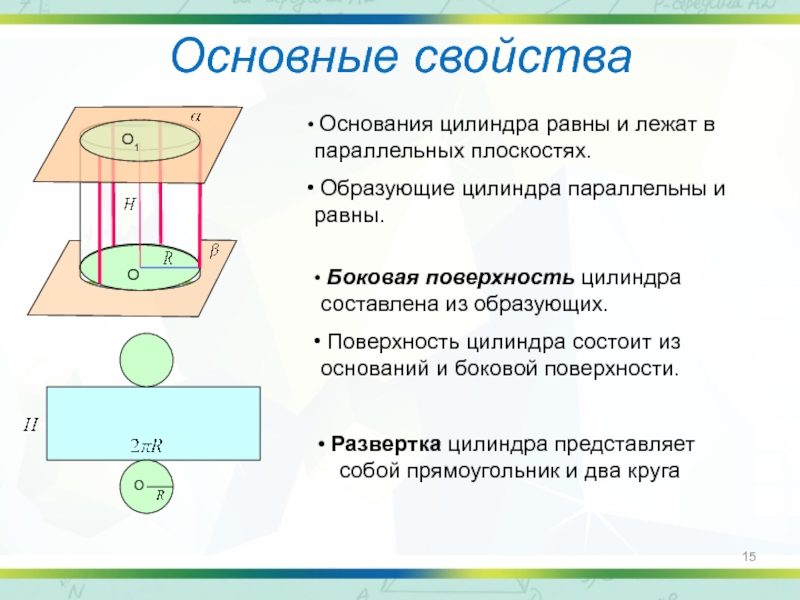
Основные свойства
Основания цилиндра равны и лежат в параллельных плоскостях.
Образующие
Боковая поверхность цилиндра составлена из образующих.
Поверхность цилиндра состоит из оснований и боковой поверхности.
O
Развертка цилиндра представляет собой прямоугольник и два круга
O1
Слайд 16
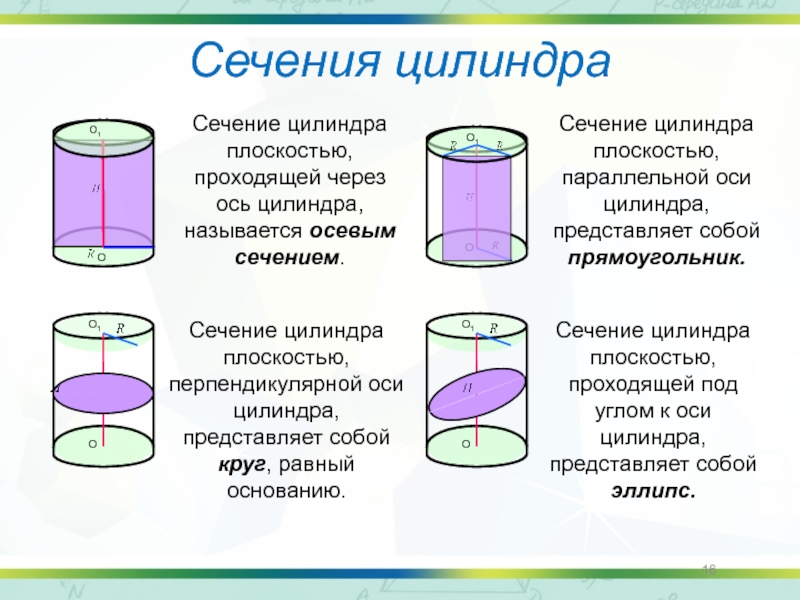
Сечения цилиндра
Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
O
O
O1
Сечение цилиндра плоскостью, параллельной оси цилиндра, представляет собой прямоугольник.
Сечение цилиндра плоскостью, перпендикулярной оси цилиндра, представляет собой круг, равный основанию.
Сечение цилиндра плоскостью, проходящей под углом к оси цилиндра, представляет собой эллипс.
O1
O1
O1
O
O
Слайд 17Основные формулы:
R - радиус основания; H - высота
Площадь полной поверхности:
Площадь боковой поверхности:
Площадь основания:
Объем цилиндра:
R
O
H
O1
Слайд 18Конус
Это тело, полученное при вращении прямоугольного треугольника вокруг оси, содержащей его
Слайд 19
Вершиной конуса называется точка, не лежащая в плоскости этого круга.
Радиусом конуса
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания.
Осью прямого конуса называется прямая, содержащая его высоту.
А
В
Н
Основанием конуса называется круг, полученный в результате вращения катета, перпендикулярного стороне, принадлежащей оси вращения.
Образующими конуса называются отрезки, соединяющие вершину конуса с точками окружности основания.
R
О
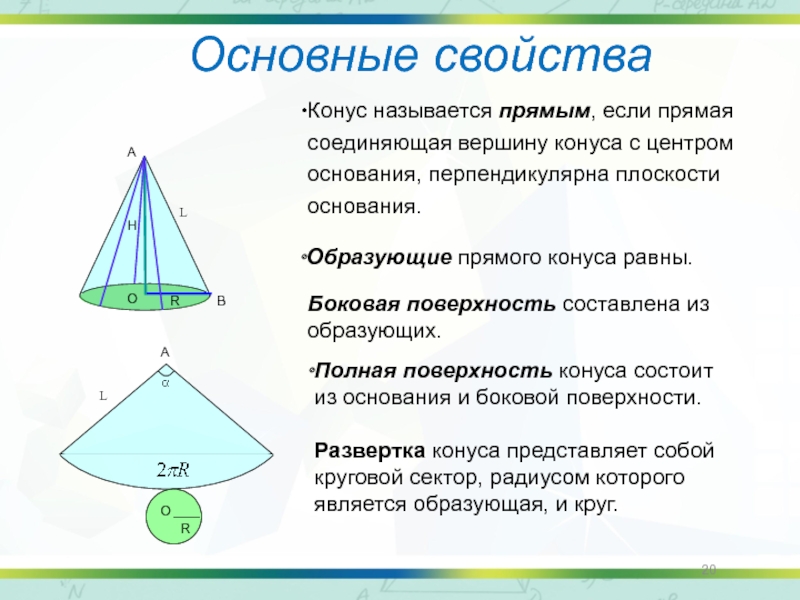
Слайд 20Основные свойства
Полная поверхность конуса состоит из основания и боковой поверхности.
Конус
Боковая поверхность составлена из образующих.
Развертка конуса представляет собой круговой сектор, радиусом которого является образующая, и круг.
А
В
Н
R
О
L
Образующие прямого конуса равны.
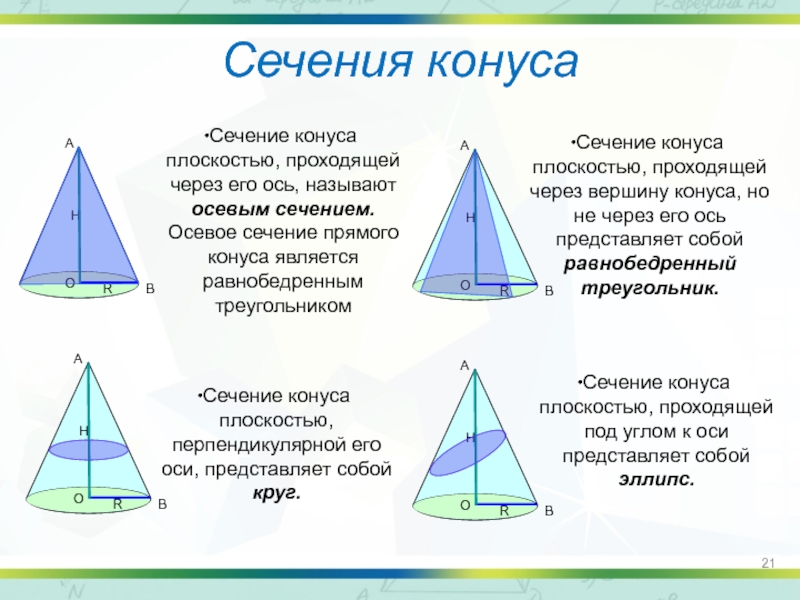
Слайд 21Сечения конуса
Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением.
Сечение конуса плоскостью, проходящей через вершину конуса, но не через его ось представляет собой равнобедренный треугольник.
Сечение конуса плоскостью, перпендикулярной его оси, представляет собой круг.
Сечение конуса плоскостью, проходящей под углом к оси представляет собой эллипс.
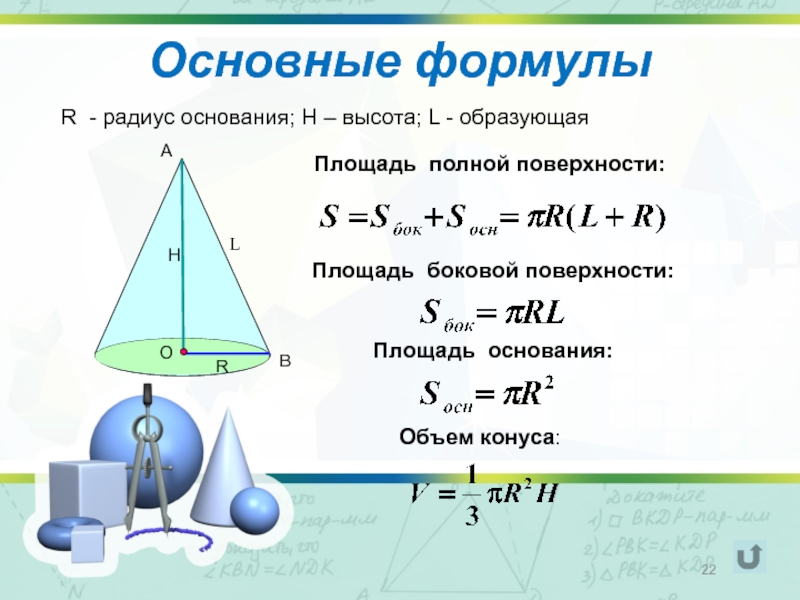
Слайд 22Основные формулы
R - радиус основания; Н – высота; L - образующая
L
Площадь
Площадь боковой поверхности:
Площадь основания:
Объем конуса:
А
В
Н
R
О
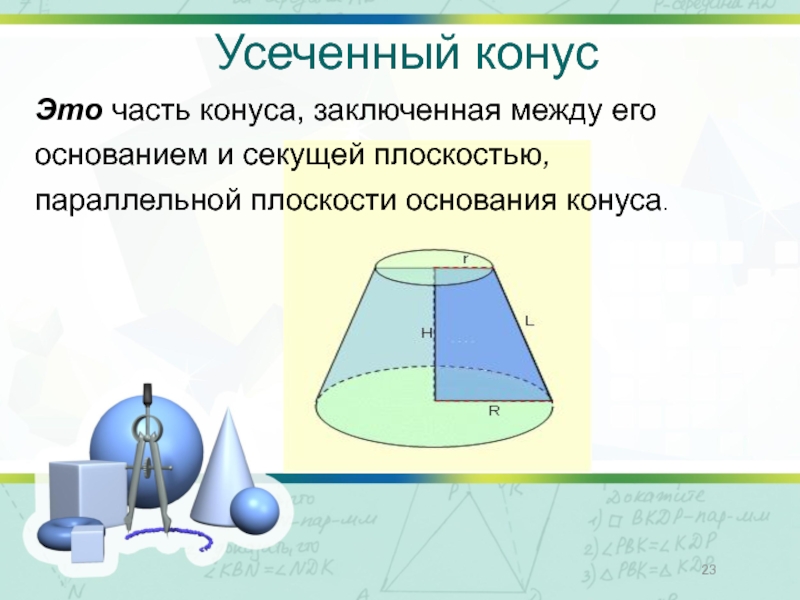
Слайд 23Усеченный конус
Это часть конуса, заключенная между его основанием и секущей плоскостью,
Слайд 24
Основные определения
Основаниями усеченного конуса называются основание данного конуса и круг, полученный
Высотой называется отрезок, соединяющий центры оснований усеченного конуса.
Образующими называются отрезки образующих конической поверхности, расположенные между основаниями усеченного конуса.
Радиусами усеченного конуса называются радиусы его оснований.
Н
L
R
r
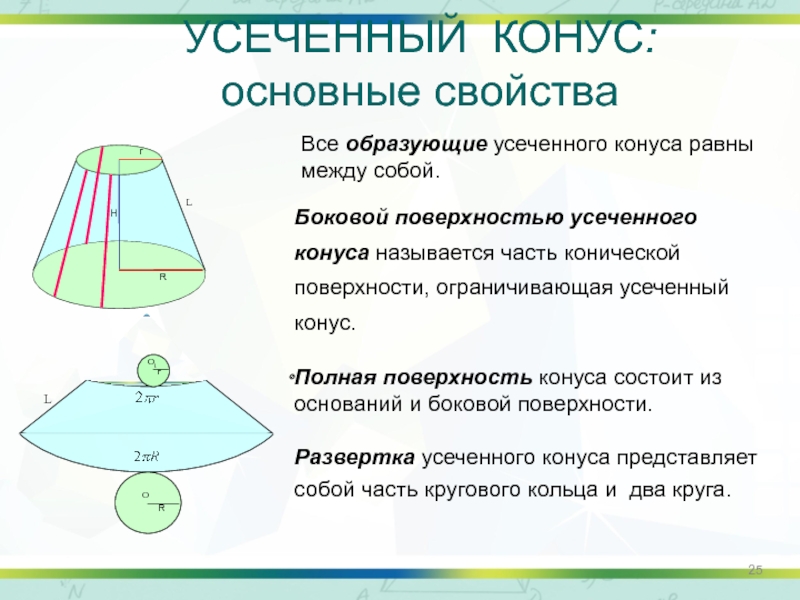
Слайд 25УСЕЧЕННЫЙ КОНУС:
основные свойства
Все образующие усеченного конуса равны между собой.
Боковой
Н
L
r
R
Полная поверхность конуса состоит из оснований и боковой поверхности.
Развертка усеченного конуса представляет собой часть кругового кольца и два круга.
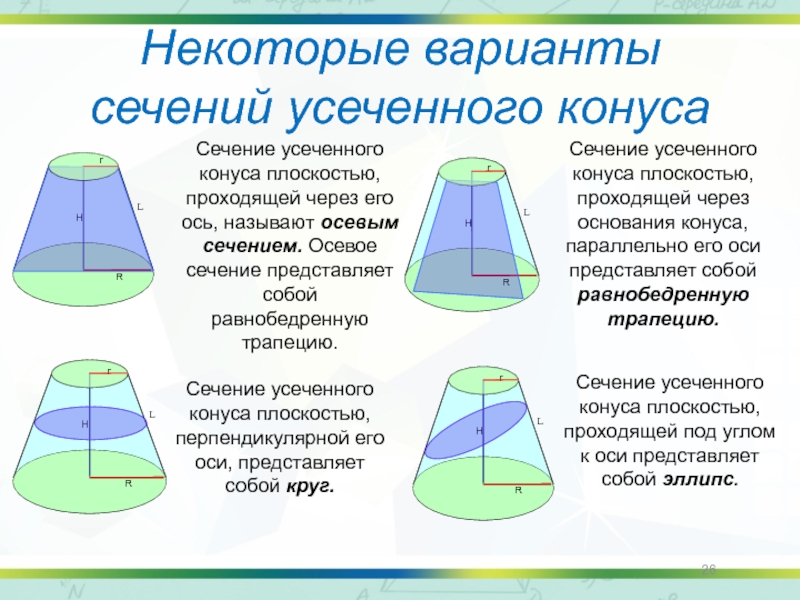
Слайд 26Некоторые варианты сечений усеченного конуса
Н
L
R
Н
L
R
Сечение усеченного конуса плоскостью, проходящей под углом
Сечение усеченного конуса плоскостью, перпендикулярной его оси, представляет собой круг.
Сечение усеченного конуса плоскостью, проходящей через основания конуса, параллельно его оси представляет собой равнобедренную трапецию.
Сечение усеченного конуса плоскостью, проходящей через его ось, называют осевым сечением. Осевое сечение представляет собой равнобедренную трапецию.
r
r
Слайд 27Основные формулы:
R и r - радиусы оснований; Н – высота; L
Площадь полной поверхности:
Площадь боковой поверхности:
Площадь оснований:
Объем усеченного конуса:
Слайд 28Сфера и шар
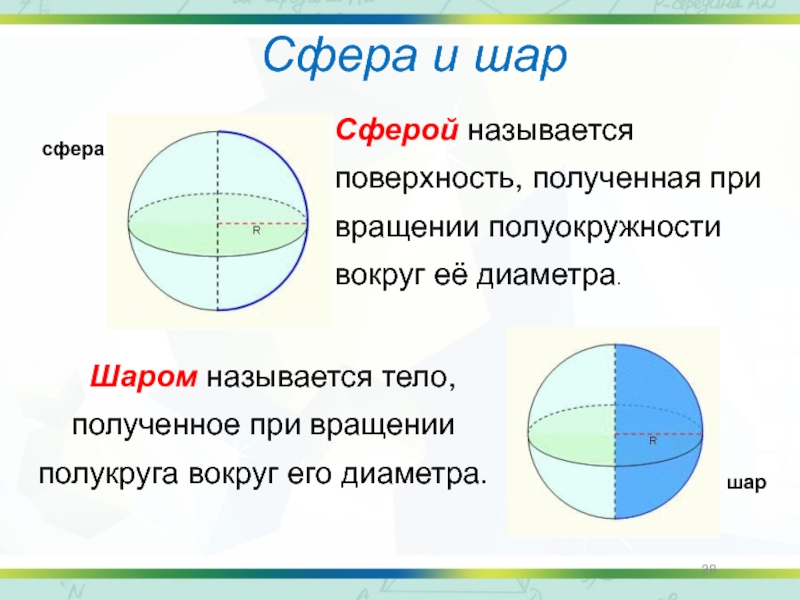
Шаром называется тело, полученное при вращении полукруга
Сферой называется поверхность, полученная при вращении полуокружности вокруг её диаметра.
шар
сфера
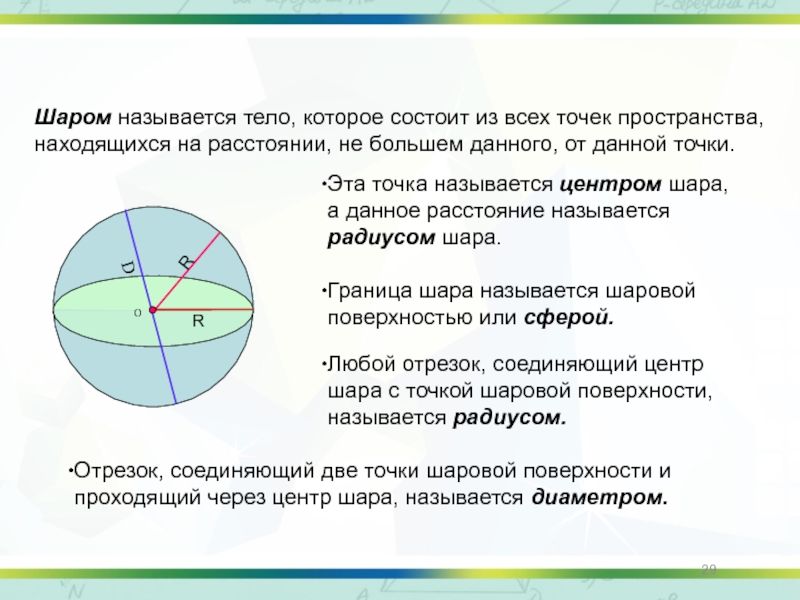
Слайд 29Шаром называется тело, которое состоит из всех точек пространства, находящихся на
Эта точка называется центром шара, а данное расстояние называется радиусом шара.
Граница шара называется шаровой поверхностью или сферой.
Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром.
R
R
R
D
O
R
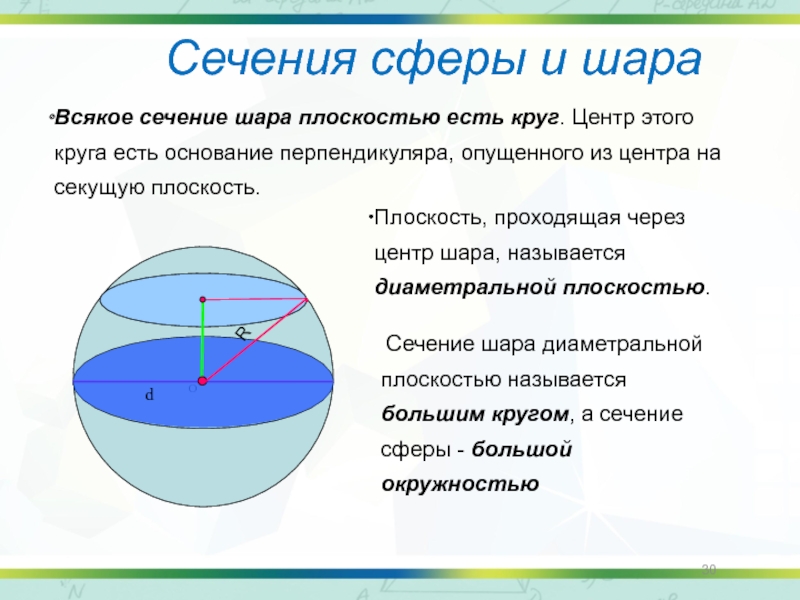
Слайд 30Плоскость, проходящая через центр шара, называется диаметральной плоскостью.
R
R
O
Сечения сферы и
Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра на секущую плоскость.
d
R
Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы - большой окружностью
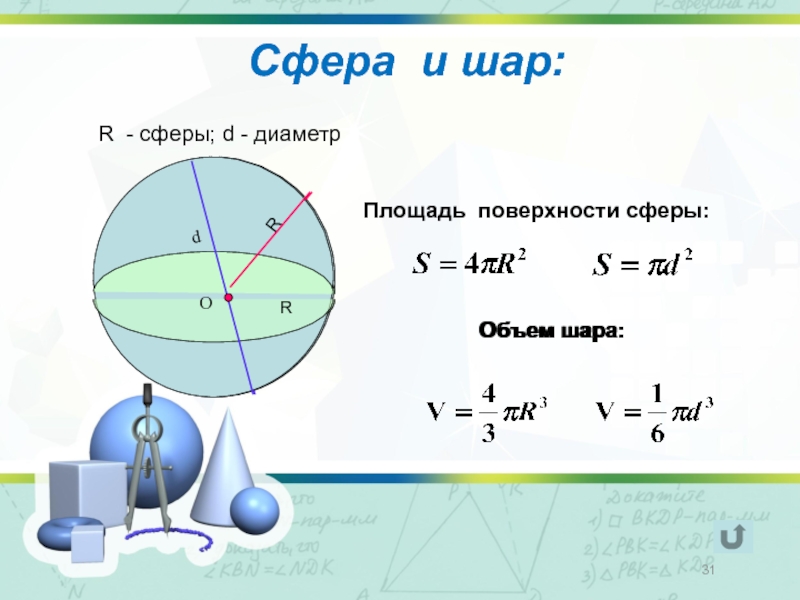
Слайд 31Сфера и шар:
R - сферы; d - диаметр
Площадь поверхности сферы:
Объем шара:
R
R
R
d
O
R
Объем шара:
R
R
R
d
O
R
Слайд 34
Задача 1. Токарю надо выточить деталь в форме цилиндра высотой 5
Дано: цилиндр,
V=140 см3 , h =5 см
Найти: R
Решение
Слайд 35Задача 2. Ведро имеет форму усеченного конуса, радиусы оснований которого равны
R
Слайд 36Задача Сколько кожи пойдет на покрытие футбольного мяча радиуса 10см (на
R
O
Слайд 37Задача Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной
Слайд 38Задача Стаканчик для мороженого конической формы имеет глубину 12см и диаметр
Ответ: нет